复杂化学

在 Simcenter STAR-CCM+ 中，使用刚性 CVODE ODE（常微分方程）求解器求解详细的复杂化学，从而对化学源项进行积分。考虑到湍流对燃烧的影响，还可以选择层流火焰概念 (LFC) 模型或涡耗散概念 (EDC) 模型。

复杂化学模型适用于将详细的化学信息引入 CFD 模拟。此模型可求解数百个组分中的数千个反应，因此称为复杂化学。由于使用 ODE 求解器对化学源项进行积分，因此复杂化学模型可以处理刚性反应系统（具有各种不同反应时间尺度的反应系统）。

在每个计算网格单元中应用于对化学源项进行积分的模型为恒压反应器。

反应系统

复杂化学模型需要有关组分、反应、热力学和传输属性的详细反应机制信息。这些详细信息由使用复杂化学模型以 Chemkin 格式导入的复杂化学定义文件提供。

源项定义

常规组分传输方程可设定为如下：

图 1. EQUATION_DISPLAY

\frac{\partial}{\partial t} ρ Y_{i} + \frac{\partial}{\partial x_{j}} (ρ {u_{j} Y}_{i} + F_{k, j}) = ω_{i}

(3410)

其中， $F_{k, j}$ 为扩散通量组分，且源项 $ω_{i}$ 为组分 $i$ 的生成率。

此算子分裂算法将利用化学反应和流场涉及的不同时间尺度。化学状态（组分质量分数 $Y_{i}$ 和温度 $T$ ）的时间积分将分两步执行：

在每个 CFD 网格单元中，每个时间步开始时，化学状态将从状态 ${(Y_{i}, T, p)}^{n}$ 到 ${(Y_{i}, T, p)}^{*}$ 进行积分，且仅用于化学源项：
图 2. EQUATION_DISPLAY

$Y_{i}^{*} = Y_{i} + \int_{0}^{τ} r_{k} (Y, T, p) d t$

(3411)
其中， $Y_{i}^{*}$ 为刚性 ODE 求解器时间积分结束时的质量分数 $τ$ （如同使用 Eqn. (3411) 进行计算）。 $r_{k}$ 为Eqn. (3358)中的反应率， $Y$ 为质量分数矢量， $T$ 为温度。
使用刚性 CVODE 求解器对 Eqn. (3411) 方程组进行求解。
组分传输方程将使用下式给出的第 $i$ 个组分的显式反应源项 $ω_{i}$ 进行求解：
图 3. EQUATION_DISPLAY

$ω_{i} = ρ f (\frac{Y_{i}^{*} - Y_{i}}{τ})$

(3412)
其中， $ρ$ 为密度， $f$ 为平均反应率乘数， $Y_{i}$ 表示单元网格中的当前质量分数。时间积分 $τ$ 指定用于非稳态模拟，并作为稳态模拟的停留时间 $τ_{r e s}$ ，如Eqn. (3328)中定义。

对于非稳态模拟，必须保持低库朗数，以确保算子分裂格式中的任何误差均为较小值。

层流火焰概念 (LFC) 和涡耗散概念 (EDC) 通过提高的湍流扩散率（由湍流模型提供）隐式考虑湍流对燃烧的影响。

对于预混火焰，此提高的扩散率将导致火焰厚度大于层流火焰厚度，且湍流火焰传播速度快于层流火焰速度。火焰厚度和速度通过湍流施密特数和普朗特数（将这些数设为彼此相等）来控制。

除了湍流扩散率的这种隐式湍流效应之外，EDC 模型还考虑组分化学源中的“湍流化学相互作用”。对于 LFC 和 EDC，组分传输方程中的平均组分源项建模为Eqn. (3412)。

对于 LFC 模型，平均反应率乘数 $f$ （在 Eqn. (3412) 中）为 1，时间尺度 $τ$ （在 Eqn. (3412) 中）为单元格中的停留时间，计算方法为 Eqn. (3328)。
对于 EDC 模型，平均反应率乘数 $f$ （在 Eqn. (3412) 中）的计算如下：
图 4. EQUATION_DISPLAY

$f = {({[C_{l} {(\frac{υ τ_{t u r b}}{L^{2}})}^{0.25}]}^{- 3} - 1)}^{- 1}$

(3413)

其中， $C_{l}$ 为精细结构长度常数（默认值为 2.1377）， $υ$ 为运动粘度， $τ_{t u r b}$ 为湍流时间尺度， $L$ 为湍流长度尺度。

对于 EDC 模型，时间尺度 $τ$ （在 Eqn. (3412) 中）的计算如下：
图 5. EQUATION_DISPLAY

$τ = τ_{t u r b}$

(3414)

其中， $τ_{t u r b}$ 为湍流时间尺度，计算方法为一个常数（默认值为 0.4082）乘以 Kolmogorov 湍流时间尺度（定义为 $\sqrt{\frac{ν}{ε}}$ ）。

Eqn. (3411) 和 Eqn. (3412) 方程表示网格单元中的组分在时间步 $τ$ 中的平均变化率。LFC 时间步约为网格单元中的停留时间 Eqn. (3328)。Eqn. (3414)中的 EDC 时间步接近 Kolmogorov 时间尺度 $τ_{k}$ （如相间湍流传输一节中所述），后者是最小湍流涡的时间尺度模型。由于 Kolmogorov 时间通常小于停留时间，且 Eqn. (3413) 中的 EDC 平均反应率乘数 $f$ 小于 1，因此与 LFC 相比，EDC 通常将湍流的效应建模为平均反应率的减小。
化学平衡的松弛法假设化学成分按照由流体和化学时间尺度确定的时间尺度松弛到局部平衡成分。可以选择使用 ISAT 计算平衡成分。
化学源项根据指定的燃料组分计算得出：
图 6. EQUATION_DISPLAY

$ω_{i} = ρ \frac{Y_{i} - Y_{i}^{e q}}{τ_{c h a r}}$

(3415)
其中， $Y_{i}$ 为组分 $i$ 的质量分数， $Y_{i}^{e q}$ 为组分 $i$ 的局部瞬时热力学平衡质量分数， $τ_{c h a r}$ 为特征时间比例：
- 使用湍流火焰速度封闭 (TFC) 模型以外的模型时：
  图 7. EQUATION_DISPLAY
  
  $τ_{c h a r} = τ_{f l o w} + τ_{c h e m}$
  
  (3416)
  
  其中：
  - $τ_{f l o w} = k / (ε c_{f l o w})$ ，其中， $ε$ 为湍流耗散率， $k$ 为湍动能， $c_{f l o w}$ 为湍流速率常数，默认值为 4。
    对于层流 $τ_{f l o w} = Δ / ({U c}_{f l o w})$ ，其中 $Δ$ 为网格尺寸， $U$ 为局部速度。
  - $τ_{c h e m} = c_{c h e m} \min_{f} (\frac{Y_{f}}{r_{f}})$ ，其中 $c_{c h e m}$ 是默认值为 2 的模型常数， $f$ 是用户指定的燃料组分列表的索引， $\min_{f}$ 取所有用户指定燃料组分的最小值， $Y_{f}$ 是 CFD 网格单元中的燃料组分质量分数，而 $r_{f}$ 是组分 $f$ 的净反应率。
- 使用 TFC 模型时：
  图 8. EQUATION_DISPLAY
  
  $τ_{c h a r} = c_{t} τ_{k}$
  
  (3417)
  其中 $c_{t}$ 为时间尺度常数， $τ_{t}$ 为 Kolmogorov 湍流时间尺度，如 $\sqrt{\frac{ν}{ε}}$ 所定义。

求解步骤

在 Simcenter STAR-CCM+ 中，可结合使用 CVODE 求解器与算子分裂算法求解反应组分输运方程，从而找到消除刚度的平均反应率。使用稳态模型运行时，将引入人工化学时间步，该时间步基于该网格单元中的对流和扩散通量。

在稳态模拟中，每个网格单元 $p$ 的化学积分时间步 $τ$ 由下式确定：

图 9. EQUATION_DISPLAY

τ = \frac{V_{p} ρ_{p}}{A_{p}}

(3418)

图 10. EQUATION_DISPLAY

= \frac{m}{\dot{m}}

(3419)

图 11. EQUATION_DISPLAY

= τ_{r e s}

(3420)

这是网格单元体积 $V_{p}$ 、密度 $ρ_{p}$ 和中心系数 $A_{p}$ （由离散化和线性化得出）的函数。Eqn. (3418) 大约为网格单元中的停留时间 Eqn. (3328)。

复杂化学模型使用 CVODE 求解器对某个时间步的刚性化学进行积分。

在 CVODE 求解器中积分的方程与恒压反应器对应：

图 12. EQUATION_DISPLAY

\frac{d Y_{k}}{d t} = \frac{{\dot{ω}}_{k}}{ρ}

(3421)

图 13. EQUATION_DISPLAY

\frac{d T}{d t} = - \frac{Σ_{k = 1}^{n} {\dot{ω}}_{k} h_{k}}{ρ C_{p}}

(3422)

其中，

t

为时间，

Y_{k}

为质量分数，

T

为温度，

{\dot{ω}}_{k}

为组分

k

的净反应率，由 Eqn. (3362) 给出，

n

为组分数，

ρ

为密度，

h_{k}

为焓，

C_{p}

为比热。

通过使用雅可比矩阵在网格单元条件下进行积分来求解常微分方程，可计算给定 CFD 网格单元中的平均组分质量分数和温度的演变过程：

图 14. EQUATION_DISPLAY

Y_{i} = Y_{i} (t_{0}) + \int_{0}^{τ_{r e s}} {\dot{ω}}_{i (t)} d t

(3423)

雅可比

J_{ω}

定义为：

图 16. EQUATION_DISPLAY

J_{ω} = \frac{\partial ω}{\partial Y}

(3425)

对于

n

组分，雅可比矩阵写为：

图 17. EQUATION_DISPLAY

J_{ω} = [\begin{matrix} \frac{\begin{matrix} \partial ω_{1} \end{matrix}}{\partial Y_{1}} & \frac{\begin{matrix} \partial ω_{1} \end{matrix}}{\partial Y_{2}} & \dots & \frac{\begin{matrix} \partial ω_{1} \end{matrix}}{\partial Y_{n}} \\ \frac{\begin{matrix} \partial ω_{2} \end{matrix}}{\partial Y_{1}} & \frac{\begin{matrix} \partial ω_{2} \end{matrix}}{\partial Y_{2}} & \dots & \frac{\begin{matrix} \partial ω_{2} \end{matrix}}{\partial Y_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \frac{\begin{matrix} \partial ω_{n} \end{matrix}}{\partial Y_{1}} & \frac{\begin{matrix} \partial ω_{n} \end{matrix}}{\partial Y_{2}} & \dots & \frac{\begin{matrix} \partial ω_{n} \end{matrix}}{\partial Y_{n}} \end{matrix}]

(3426)

数值雅可比表示使用有限差分法针对系统中的每个组分衍生得出的雅可比。由于化学源项 $ω$ 随 CVODE 求解器迭代而重复计算，因此求解 ODE 的成本十分高昂。

根据链式法则计算分析雅可比可获得 $J_{ω}$ 的分析表达式。

由于此过程的计算成本较高，因此使用 ISAT、聚类或动力机制减少以降低成本并加速达到收敛求解。

ISAT

原位自适应制表 (ISAT) 以表格形式动态列出计算成本较高的函数，并在制表后多次进行插值[766]。ISAT 方法通过以下各项为给定的初始条件提供 ODE 近似求解 (Eqn. (3411))：

热力学变量（温度或总焓）。
成分变量（质量分数或摩尔数）。
可能包括压力和时间步（取决于模拟类型）。

这些值构成自变量或查询点 (

ϕ

)。ODE 方程 (Eqn. (3411)) 的求解

f

称为反应映射。

ISAT 方法从空表开始，逐步向其中添加点。要求解

ϕ_{0}

的第一个 ODE 方程（第一次查询），ISAT 执行以下操作：

调用 ODE 求解器来计算 $f_{0}$ 。
创建一项并将其添加到表中。

每个表项均包含：

独立变量 $ϕ$
反应映射变量 $f$
映射梯度矩阵 $A = \frac{\partial f}{\partial ϕ}$
误差椭圆 (EOA)，衍生自映射梯度的奇异值分解。

对于所有后续查询，ISAT 对查询点

ϕ_{n}

执行以下操作：

遍历表并查找合适的点，检查可能的近似。
对于合适的点 $ϕ_{t}$ ，它将检查值： $f_{q} = f_{t} + A_{t} (ϕ_{n} - ϕ_{t})$

可能会出现以下两种情景：

$f_{q}$ 位于 EOA 中，这意味着值 $f_{q}$ 在用户指定的容差内，近似于 $f (ϕ_{n}))$ 的真实值。换言之，将检索查询 $ϕ_{n}$ 。
或者， $f_{q}$ 位于 EOA 之外。在这种情况下，将计算 $f (ϕ_{n}))$ 的真实值并推导得出两个值之差。如果此差值小于用户自定义的容差，这意味着 $ϕ_{n}$ 点处的 EOA 太过严苛。在这种情况下，椭圆体会增长以接受 $f_{q}$ 点。如果此差值高于指定的容差，该点将添加到表中。

表中的点存储在二进制空间分区树的分支中。为了加快搜索，此树将点目前在

n

维空间（

n

是查询点的维度）中占据的区域分成若干更小的子区域。将新的查询点添加到树中时，原始分支现在由超平面一分为二。一个新分支包含旧点，位于超平面的一侧。第二个新分支包含新的查询点，位于超平面的另一侧。

因此，以下属性可体现 ISAT 方法的特征：

检索次数：近似反应映射的查询数量
增长次数：计算反应映射的查询数量，但是该点不添加到表中，因为表中的旧点的 EOA 已增长
添加次数：计算反应映射的查询数量，且该点已添加到表中

可以通过 ISAT 近似法内的属性停用 EOA 增长。由于 EOA 只是实际精度范围的近似值，因此 EOA 增长可能导致近似表出错。此外，与增长现有 EOA 相比，向表中添加点可能会涵盖更多未来的查询。

聚类

聚类对具有相似化学成分的网格单元求平均值，并整合减少的 ODE 集合，然后将集群再次插值到网格单元中，以此减少计算复杂化学的计算开销。

通过几个成分变量，可形成维度较低且间隔均匀的聚类网格。默认情况下，Simcenter STAR-CCM+ 使用两个聚类变量（当量比和温度）进行非稳态模拟。对于稳态模拟，化学时间尺度的对数还用作额外的聚类变量。

聚类容差可确定聚类网格点之间的聚类成分变量距离。对于相对容差

ε_{r e l}

，聚类成分变量的网格点数

ϕ

为：

图 21. EQUATION_DISPLAY

\frac{1}{ε_{r e l}}

(3430)

对于绝对容差

ε_{a b s}

，聚类成分变量的网格点数

ϕ

为：

图 22. EQUATION_DISPLAY

\frac{ϕ_{\max} - ϕ_{\min}}{ε_{a b s}}

(3431)

其中，

ϕ_{\max}

和

ϕ_{\min}

表示计算域中

ϕ

的最大值和最小值。

根据 Babajimopolous[750]，聚类当量比定义为：

图 23. EQUATION_DISPLAY

ϕ = \frac{2 C^{*} + \frac{H^{*}}{2}}{O^{*}}

(3432)

其中：

$C^{*}$ 为除 ${C O}_{2}$ 以外的所有组分中的 $C$ 原子数，乘以组分质量分数并除以组分分子量。
$H^{*}$ 为除 $H_{2} O$ 以外的所有组分中的 $H$ 原子数，乘以组分质量分数并除以组分分子量。
$O^{*}$ 为除 ${C O}_{2}$ 和 $H_{2} O$ 以外的所有组分中的 $O$ 原子数，乘以组分质量分数并除以组分分子量。

除了默认聚类变量之外，还可以选择额外聚类变量，例如，混合分数和组分。聚类混合分数定义为混合物中氢和氧原子的元素质量分数。

在每个聚类网格点内，组分质量分数、能量、压力和（对于稳态）化学时间步均会进行网格单元质量加权平均计算，以求出集群平均值。此成分（Eqn. (3411) 中的

Y_{i}^{*}

）使用 CVODE 求解器求积分，如 Eqn. (3411) 中所示。随后，源项将应用于集群中的所有网格单元。

动态机理简化

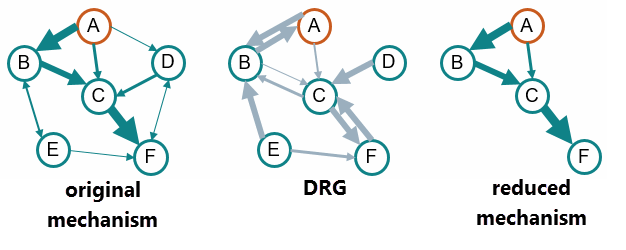
通过动力机制减少，Simcenter STAR-CCM+ 中的 CVODE 求解器可以求解完整化学机制中减少的组分数量。定向关系图 (DRG) 算法 [755] 考虑每个时间步或每次迭代的网格单元中所有组分的反应率，如果组分在时间步中对任何其他组分的生成/破坏影响甚微，则会从机制中移除这些组分。

决定能否从完整化学机制中移除某个组分时，DRG 算法会考虑该组分对其他组分的生成率有何显著影响。

对于任何组分 A，移除组分 B 对组分 A 生成率的影响如下：

图 24. EQUATION_DISPLAY

r_{A B} = \frac{\max_{i} | ν_{A, i} ω_{i} δ_{B, i} |}{\max_{i} | ν_{A, i} ω_{i} |}

(3433)

如果第 $i$ 次基础反应涉及组分 B， $δ_{B, i} = 1$
如果第 $i$ 次基础反应不涉及组分 B， $δ_{B, i} = 0$

当组分 B 对组分 A 的生成率的归一化贡献 (

r_{A B}

) 大于指定的误差容差

ε

时，DRG 算法还会保留组分 B。组分 A 和 B 被视为强烈耦合，移除组分 B 将会对组分 A 的生成率产生显著影响。

DRG 中的每个节点（下图中的 A 到 F）均表示完整化学机制中的组分。

上图中的所有箭头均表示定向边，这些边是 DRG 中位于具有依赖性的组分之间的边。箭头显示某个组分对另一个组分的依赖性方向，宽度表示依赖性的强度。由于 A 依赖于 B 和 C，且 C 依赖于 F，因此 A、B、C 及 F 的组分组均必须保留才能正确计算 A。剩余的组分可以移除，因为它们对 A 的生成率没有显著影响。