化学动能

化学动能涉及化学组分在分子级别的反应机制和反应率。

对反应组分输运进行建模时，为传输方程提供源项需要计算化学机制中所有反应的反应率（化学动能）。

任何基元化学反应均可用以下常规方程表示。

图 1. EQUATION_DISPLAY

υ_{A}^{'} A + υ_{B}^{'} B + ... ⇌_{k_{b}}^{k_{f}} υ_{C}^{''} C + υ_{D}^{''} D + ...

(3353)

其中，带上标 ' 的化学计量系数

υ

表示反应物，带 '' 的系数表示产物。净化学计量系数

υ_{i j}

给出反应

j

产生或消耗的组分

i

的摩尔总数：

图 2. EQUATION_DISPLAY

υ_{i j} = υ_{i}^{''} - υ_{i}^{'}

(3354)

反应可以正向进行（即，反应物变为产物）或逆向进行（即，产物形成反应物）。

k_{f}

为正反应率常数，

k_{b}

为逆反应率常数。

k

为同时考虑

k_{f}

和

k_{b}

的总速率常数。

图 3. EQUATION_DISPLAY

k = k_{f} - k_{b}

(3355)

反应率

基元反应的反应率计算如下。

以反应机制中的一个反应为例：

图 4. EQUATION_DISPLAY

2 CO + O_{2} \overset{k}{\leftrightarrow} 2 {CO}_{2}

(3356)

有两种反应物组分和一种产物组分。要使反应继续下去，反应物分子必须与等于或大于激活能 $E_{a}$ 的能量碰撞。总体反应率 $r_{k}$ 还取决于速率常数 $k$ 和两种反应物的浓度（是其化学计量系数的次幂）。

Eqn. (3356) 的速率方程写作：

图 5. EQUATION_DISPLAY

r_{k} = k_{f} {[CO]}^{2} [O_{2}] - k_{b} {[{CO}_{2}]}^{2}

(3357)

对于常规反应，Eqn. (3353)，这表示为：

图 6. EQUATION_DISPLAY

r_{k} = k_{f} {[A]}^{υ_{A}^{'}} {[B]}^{υ_{B}^{'}} ... - k_{b} {[C]}^{υ_{C}^{''}} {[D]}^{υ_{D}^{''}} ...

(3358)

方括号中组分的化学式表示该组分在反应混合物中的浓度。

通过将反应率乘以净化学计量系数 Eqn. (3354)，计算反应的每个组分的变化率。例如，Eqn. (3356) 中 CO 的反应率为：

图 7. EQUATION_DISPLAY

\frac{d [C O]}{d t} = 2 (- k_{f} \cdot {[C O]}^{2} [O_{2}] + k_{b} {[{C O}_{2}]}^{2})

(3359)

对于常规一步反应，Eqn. (3353)，这表示为：

图 8. EQUATION_DISPLAY

\frac{d [A]}{d t} = υ_{A} [k_{f} \cdot {[A]}^{υ_{A}^{'}} {[B]}^{υ_{B}^{'}} ... - k_{b} {[C]}^{υ_{C}^{''}} {[D]}^{υ_{D}^{''}} ...]

(3360)

其中

υ_{A} = υ_{A}^{''} - υ_{A}^{'}

(3361)

组分 $i$ 的生成（或消耗）率 $r_{i}$ 取决于生成和消耗该组分的反应的反应率以及参与这些反应的所有组分的浓度。因此，总净速率为组分 $i$ 参与的所有反应的 Eqn. (3360) 之和。在以下方程中， $j$ （= 1、2… $N_{j}$ ）表示反应， $i$ 表示组分。

组分 i 的净反应率，表示为 ${\dot{ω}}_{i}$ ，是所有反应（ $r_{j}$ ，位于 Eqn. (3358)）之和乘以化学计量系数。

图 9. EQUATION_DISPLAY

{\dot{ω}}_{i} = \frac{d [A]}{d t} = \sum_{j = 1}^{N_{j}} υ_{i j} r_{j}

(3362)

图 10. EQUATION_DISPLAY

r_{j} = k_{f, j} \underset{i}{Π} {[A]}^{υ_{j, i}^{'}} - k_{b, j} \underset{i}{Π} {[A]}^{υ_{j, i}^{''}}

(3363)

其中，正反应率系数 $k_{f}$ 和逆反应率系数 $k_{b}$ 由 Eqn. (3365) 确定。

用户定义反应率的计算方法如下：

图 11. EQUATION_DISPLAY

r_{j} = k_{j} \underset{i}{Π} {[A]}^{υ_{j, i}^{'}}

(3364)

其中，

k_{j}

为反应

j

的用户反应系数。

速率常数

k

通常使用阿雷尼乌斯方程确定，其中速率与温度非线性相关：

图 12. EQUATION_DISPLAY

k = A T^{β} \exp (- \frac{E_{a}}{R_{u} T})

(3365)

其中，

R_{u}

为通用气体常数，以下值为化学机制提供的经验因子：

温度指数 $β$
活化能 $E_{a}$
频率因子或指前因子 $A$

化学放热率

化学放热率定义为：

图 13. EQUATION_DISPLAY

\dot{h} = \sum {\dot{ω}}_{k} h_{k}^{o}

(3366)

其中， ${\dot{ω}}_{k}$ 为 $k' t h$ 组分的净反应率， $h_{k}^{o}$ 为 $k' t h$ 组分的形成焓。使用组分输运模型时，Eqn. (3366) 可作为名为 Chemical Heat Release Rate（化学放热率）的场函数计算和提供。

对于小火焰生成流形 (FGM) 以及部分预混化学平衡 (CE) 和稳态层流小火焰 (SLF) 模型，化学放热率计算如下：

图 14. EQUATION_DISPLAY

\dot{h} = \dot{c} h_{R}

(3367)

其中， $\dot{c}$ 为进程变量源项， $h_{R}$ 为反应热。 $h_{R}$ 的计算需要假设燃料在一步反应中与氧气发生碳氢化合物反应：

图 15. EQUATION_DISPLAY

C_{n} H_{m} + (n + \frac{m}{4}) O_{2} \to n C O_{2} + \frac{m}{2} H_{2} O

(3368)

反应热计算如下：

图 16. EQUATION_DISPLAY

h_{R} = \sum Y_{k}^{F} h_{k}^{o} - n h_{C O 2}^{o} - \frac{m}{2} h_{H 2 O}^{o}

(3369)

其中， $Y_{k}^{F}$ 为燃料流中的 $k' t h$ 组分的质量分数。

对于非预混 SLF，化学放热率计算如下：

图 17. EQUATION_DISPLAY

\dot{h} = χ h_{R}

(3370)

其中， $χ$ 为标量耗散率。

注意，小火焰模型的化学放热率近似 Eqn. (3366) 中的精确放热率，场函数名为 Chemical Heat Release Rate Indicator（化学放热率指示器）。

第三体反应

第三体效率

一些反应需要“第三体”才能进行，如下所示：

图 18. EQUATION_DISPLAY

H + O_{2} + M \leftrightarrow H O_{2} + M

(3371)

其中，

M

表示第三体。第三体充当一种催化剂。通常，混合物中的任何组分均可作为第三体。第三体影响反应进行的速率。

需要第三体的反应的反应率的表达式如下：

图 19. EQUATION_DISPLAY

r_{j} = (Σ_{i = 1}^{N} (α_{i j}) [X_{i}]) (k_{f, j} Π_{i = 1}^{N} {[X_{i}]}^{υ_{i j}^{'}} - k_{b, j} Π_{i = 1}^{N} {[X_{i}]}^{υ_{i j}^{''}})

(3372)

对于组分

(i = 1, ..., N)

：

$α_{i j}$ 表示第三体的碰撞效率
$k_{f, j}$ 为反应的正向速率常数 $j$
$k_{b, j}$ 为反应的反应反向速率常数 $j$

当

α_{i j} = 1

时，混合物中的所有组分都将作为第三体同等发挥作用，混合物的总浓度为：

图 20. EQUATION_DISPLAY

[M] = Σ_{i = 1}^{N} [X_{i}]

(3373)

但是，当

α_{i j} \neq 1

时，反应中的有效第三体的浓度为：

图 21. EQUATION_DISPLAY

[M] = Σ_{i = 1}^{N} (α_{i j}) [X_{i}]

(3374)

其中，

α_{i j}

是为反应机制中的第三体组分指定的值。

压力相关化学反应率

压力相关化学反应（脱落反应）在低压下为一阶比率，随着第三体组分的浓度增加而变为零阶。在此类反应中，速率受压力和温度影响，Simcenter STAR-CCM+ 使用反应机制提供的指前因子

A

计算速率常数：

图 22. EQUATION_DISPLAY

k = k_{\infty} (\frac{P_{r}}{1 + P_{r}}) F

(3375)

其中，折算压力

P_{r}

为：

图 23. EQUATION_DISPLAY

P_{r} = \frac{k_{0} [M]}{k_{\infty}}

(3376)

其中，

[M]

为具有第三体效率的组分

M

的浓度。

低压限值

k_{0}

为：

图 24. EQUATION_DISPLAY

k_{0} = A_{0} T^{β 0} \exp (- \frac{E_{0}}{R_{u} T})

(3377)

高压限值

k_{\infty}

为：

图 25. EQUATION_DISPLAY

k_{\infty} = A_{\infty} T^{β \infty} \exp (- \frac{E_{\infty}}{R_{u} T})

(3378)

混合（脱落）函数

F

的计算方法有所不同，具体取决于指定压力相关参数所使用的方法。

使用 Lindemann 方法时， $F$ 计算为合一值， $F = 1$
使用 Troe 方法时， $F$ 计算如下：
图 26. EQUATION_DISPLAY

$\log F = {[1 + {[\frac{\log P_{r} + c}{n - d (\log P_{r} + c)}]}^{2}]}^{- 1} \log F_{c e n t}$

(3379)
其中：
图 27. EQUATION_DISPLAY

$F_{c e n t} = (1 - α) \exp (- \frac{T}{T^{* * *}}) + α \exp (- \frac{T}{T^{*}}) + \exp (- \frac{T^{* *}}{T})$

(3380)
- $c = - 0.4 - 0.67 \log F_{c e n t}$
- $n = 0.75 - 1.27 \log F_{c e n t}$
- $d = 0.14$
- $α$ 、 $T^{* * *}$ 、 $T^{*}$ 和 $T^{* *}$ 分别为在已导入的化学机制中指定的常数
使用 (SRI) 方法时， $F$ 计算如下：
图 28. EQUATION_DISPLAY

$F = d {[a \exp (\frac{- b}{T}) + \exp (\frac{- T}{c})]}^{X} T^{e}$

(3381)

其中，a、b、c、d 和 e 是在导入的化学机制中指定的常数。如果机制中未指定 d 和 e，则默认情况下会将它们分别设为 1 和 0。
图 29. EQUATION_DISPLAY

$X = \frac{1}{1 + \log^{2} P_{r}}$

(3382)

对于 Troe 和 SRI 方法，高压和低压限值的

F

都接近合一值。

化学活性双分子反应率

在化学活性双分子反应中，由于反应中间体的碰撞稳定，因此反应率随压力的增加而降低（脱落）。正反应率常数与低压速率常数成比例：

图 30. EQUATION_DISPLAY

k = k_{0} (\frac{1}{1 + P_{r}}) F

(3383)

混合函数

F

也使用 Troe、Lindemann 或 SRI 方法定义。

基于对数插值的压力依赖性 (PLOG)

使用 PLOG 方法描述反应率的压力依赖性时，可使用已针对不同压力进行修正的速率参数（ $β$ 、 $E_{a}$ 和 $A$ ）通过阿雷尼乌斯表达式 Eqn. (3365) 计算反应率。

为相关压力范围内的一组（至少两个）不同离散压力给定了速率参数。

当模拟中的压力 $P$ 介于给定压力之间（例如，介于 $P_{i}$ 和 $P_{i + 1}$ 之间）时，可通过将 $\ln k$ 线性插值为 $\ln P$ 的函数来计算速率参数：
图 31. EQUATION_DISPLAY

$\ln k = \ln k_{i} + (\ln k_{i + 1} - \ln k_{i}) \frac{\ln P - \ln P_{i}}{\ln P_{i + 1} - \ln P_{i}}$

(3384)
当模拟中的压力高于或低于任何给定压力时，分别使用最高或最低压力的速率参数。

化学平衡

当正反应率和逆反应率相等时，反应被视为已达到平衡且未观察到净反应。只要压力（对于气相反应）、温度和组分浓度保持恒定，反应物和产物的比例即为常数。

可以使用平衡常数 $K$ 确定在平衡状态下每种组分的数量。

对于常规反应，Eqn. (3353)，平衡常数定义为：

图 32. EQUATION_DISPLAY

K = \frac{{(a_{C})}^{υ_{C}^{''}} {(a_{D})}^{υ_{D}^{''}} ...}{{(a_{A})}^{υ_{A}^{'}} {(a_{B})}^{υ_{B}^{'}} ...}

(3385)

其中，

a

为相应组分的活性。气相组分（例如，组分

A

）的活性定义为：

图 33. EQUATION_DISPLAY

a_{A} = \frac{[A]}{c^{0}}

(3386)

其中， $c^{0}$ 为参考浓度。

在化学平衡状态下：

图 34. EQUATION_DISPLAY

k_{f} {[A]}^{υ_{A}^{'}} {[B]}^{υ_{B}^{'}} ... = + k_{b} {[C]}^{υ_{C}^{''}} {[D]}^{υ_{D}^{''}} ...

(3387)

也可以表示为：

图 35. EQUATION_DISPLAY

\frac{{[C]}^{υ_{C}^{''}} {[D]}^{υ_{D}^{''}} ...}{{[A]}^{υ_{A}^{'}} {[B]}^{υ_{B}^{'}} ...} = \frac{k_{f}}{k_{b}}

(3388)

对于在平衡状态下已知组分浓度的反应，相对浓度

K_{c}

的平衡常数可由下式确定：

图 36. EQUATION_DISPLAY

K_{c} = \frac{{[C]}^{υ_{C}^{''}} {[D]}^{υ_{D}^{''}}}{{[A]}^{υ_{A}^{'}} {[B]}^{υ_{B}^{'}}}

(3389)

这意味着：

图 37. EQUATION_DISPLAY

K_{c} = \frac{k_{f}}{k_{b}}

(3390)

相对浓度的平衡常数也可以使用亥姆霍兹自由能

A

根据热力学数据确定：

图 38. EQUATION_DISPLAY

K_{c} = \exp (\frac{Δ_{R} {\bar{A}}^{0}}{R_{u} T})

(3391)

或者，对于相对压力的平衡常数，使用吉布斯自由能

G

确定：

K_{p} = \exp (\frac{Δ_{R} {\bar{G}}^{0}}{R_{u} T})

(3392)

表面化学

在表面化学反应期间，可能发生三个过程：

气相分子与表面分子碰撞，然后被吸附。表面点位（表面的活性分子）成为块体的一部分，先前的气相分子在块体顶部形成新的表面。
表面上的分子之间或表面上的一个分子和气体中的一个分子之间的表面反应会形成新的表面、气相或块体分子。
分子在反应后进入气相，或者只需克服键能，即可解吸表面分子。

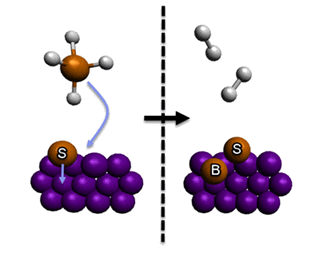
例如，在下图中，气体分子被吸附在先前吸附的表面组分旁边的表面上。气体分子分解为其构成原子。吸附的某些原子发生反应，形成离开表面的小气体分子。气体分子中的一个原子仍然作为表面组分被吸附，而先前吸附的表面组分则成为块体组分。

上图中的反应可以表示为：

Si H_{4 (G)} + {Si}_{(S)} \to {Si}_{(S)} + {Si}_{(B)} + 2 H_{2 (G)}

如果先前覆盖块体组分的表面分子被解吸或参与反应，则块体组分不会被视为活性，但最终可以位于表面点位上。

使用表面气体相互作用模型必须定义三种类型的组分：

气相中的组分， $G$
气体表面交界面处表面上的组分， $S$ 。表面反应可描述为使用开放点位形式或原子点位形式。
固体层中的组分，块体组分， $B$ 。

反应 $j$ 的通用表面反应形式如下：

图 39. EQUATION_DISPLAY

\sum_{i = 1}^{N_{g}} {g′}_{i, j} G_{i} + \sum_{i = 1}^{N_{s}} {s′}_{i, j} S_{i} + \sum_{i = 1}^{N_{b}} {b′}_{i, j} B_{i} = \sum_{i = 1}^{N_{g}} g_{i, j''} G_{i} + \sum_{i = 1}^{N_{s}} s_{i, j''} S_{i} + \sum_{i = 1}^{N_{b}} b_{i, j''} B_{i}

(3393)

其中：

$G_{i}$ 、 $S_{i}$ 和 $B_{i}$ 为气体、点位和块体组分。
$N_{g}$ 、 $N_{s}$ 和 $N_{b}$ 为气体、点位和块体组分的数量。
${g′}_{i, j}$ 、 ${s′}_{i, j}$ 和 ${b′}_{i, j}$ 为气体、点位和块体反应物的化学计量系数。
$g_{i, j''}$ 、 $s_{i, j''}$ 和 $b_{i, j''}$ 为气体、点位和块体产物的化学计量系数。

第 $j$ 个反应的速率为：

图 40. EQUATION_DISPLAY

r_{j} = k_{f, j} Π_{i = 1}^{N_{g}} {[G_{i}]}_{wall}^{{p_{g}}_{(i, j)}} Π_{i = 1}^{N_{s}} {[S_{i}]}_{wall}^{{p_{s}}_{(i, j)}}

(3394)

其中， $p_{g}$ 和 $p_{s}$ 为反应物的比率指数， ${[*]}_{wall}$ 表示壁面上的摩尔浓度。反应 $j$ 的正向速率常数 $k_{f, j}$ 由阿雷尼乌斯表达式给出。对于最简单的反应类型，该常数由 Eqn. (3365) 给出（其中， $k$ 为 $k_{f, j}$ ）。

对于第

n

种点位类型，表面组分

{[S}_{i}]

的浓度（以摩尔/平方米为单位）由点位密度

Γ_{n}

、第

i

个组分

Z_{S_{i}, n}

覆盖的点位分数和组分覆盖

σ_{S_{i}, n}

的点位数量确定。

图 41. EQUATION_DISPLAY

[S_{i}] = \underset{n}{Σ} \frac{Z_{S_{i}, n} Γ_{n}}{σ_{S_{i}, n}}

(3395)

总和将在所有不同的点位类型中运行。

假设反应率与块体组分的浓度无关。

每个组分 $i$ 每单位表面积的净摩尔变化率（结果或消耗）由以下公式给出：

图 42. EQUATION_DISPLAY

{\hat{r}}_{i, gas} = \sum_{j = 1}^{N_{r e a c}} (g_{i, j''} - {g′}_{i, j''}) r_{j}

(3396)

图 43. EQUATION_DISPLAY

{\hat{r}}_{i, site} = \sum_{j = 1}^{N_{r e a c}} (s_{i, j''} - {s′}_{i, j}) r_{j}

(3397)

图 44. EQUATION_DISPLAY

{\hat{r}}_{i, bulk} = \sum_{j = 1}^{N_{r e a c}} (b_{i, j''} - {b′}_{i, j}) r_{j}

(3398)

对于某些表面反应，反应率受所涉及组分的表面覆盖特征影响。可以修正阿雷尼乌斯速率表达式 Eqn. (3365) 来创建校正速率常数，如下所示：

点位覆盖校正率表达式
某些表面反应由组分 $i$ 的表面点位覆盖率 $z_{i}$ 体现。

图 45. EQUATION_DISPLAY

$k_{f, j} = A_{j} T^{β_{j}} \exp (- \frac{E_{a}}{R_{u} T}) Π_{i = 1}^{N_{s}} 10^{η_{i, j}} z_{i}^{μ_{i, j}} \exp (- \frac{ε_{i, j} Z_{i}}{R_{u} T})$

(3399)

其中， $η_{i, j}$ 、 $μ_{i, j}$ 和 $ε_{i, j}$ 是可为反应表面上的组分 $i$ 和反应 $j$ 指定的三个表面覆盖参数。在导入的反应机制文件中，表面覆盖修正反应由关键词 COV 表示。请参见反应机制格式。
粘附系数校正率表达式
可以使用粘附系数或粘附概率（而非反应率系数）表示正向表面反应率。粘附系数表示组分粘附到表面的概率。反应可以包括一个气相组分和任意数量的表面组分，且反应率与所有涉及的表面组分的覆盖率成比例。粘附系数 $s_{c}$ 计算如下：
图 46. EQUATION_DISPLAY

$s_{c} = \min ⌊ 1, A_{j} T^{β_{j}} e^{\frac{- E_{a, j}}{R_{u} T}} ⌋$

(3400)
速率表达式修改如下：
图 47. EQUATION_DISPLAY

$k_{f, j} = s_{c} \frac{Π_{i = 1}^{N_{s}} σ_{i}^{{υ^{'}}_{i, j}}}{{(Γ_{t o t})}^{m}} \sqrt{\frac{R_{u} T}{2 π {M_{w}}_{i}}}$

(3401)

$Γ_{t o t}$ 是总表面站点浓度、 $m$ 是所有表面反应物化学计量系数之和。 ${M_{w}}_{i}$ 为气相组分的分子量，而为每个表面组分占据的点位数 - 为该组分的反应级数。 $i$ $σ_{i}$ ${υ^{'}}_{i, j}$
Motz-Wise 校正率表达式
使用 Motz-Wise 校正因子的前向反应率表达式为：
图 48. EQUATION_DISPLAY

$k_{f, j} = (\frac{s_{c}}{1 - s_{c} / 2}) \frac{Π_{i = 1}^{N_{s}} σ_{i}^{{υ^{'}}_{i, j}}}{{(Γ_{t o t})}^{m}} \sqrt{\frac{R_{u} T}{2 π {M_{w}}_{i}}}$

(3402)
其中， $s_{c}$ 由 Eqn. (3400) 计算。
博姆校正率表达式
模拟包含正离子的反应时，可以修改速率常数来包含 Bohm 速度校正 $\sqrt{\frac{{RR}_{uu} {TT}_{ee}}{{MM}_{ww}_{ii}}}$ ，这考虑到了反应的发生概率：
图 49. EQUATION_DISPLAY

$k_{f, j, B o h m} = A_{j} T^{β_{j}} e^{- E_{a, j} / R T} \frac{Π_{i = 1}^{N_{s}} σ_{i}^{{υ^{'}}_{i, j}}}{{(Γ_{t o t})}^{m}} \sqrt{\frac{R_{u} T_{e}}{{M_{w}}_{i}}}$

(3403)

其中为电子温度，而为正离子的分子量。 $T_{e}$ ${M_{w}}_{i}$
Langmuir-Hinshelwood
Langmuir-Hinshelwood 为全局表面反应，将组分吸附、表面反应和解吸合并到单个步骤中。Langmuir-Hinshelwood 全局速率表达式适用于假设吸附和解吸处于平衡状态，并且表面上吸附组分之间的反应决定速率的情况。假设表面上的吸附点位相互独立（单点位吸附），则这些点位是等效的，并且表面覆盖仅会减少可供吸附的点位数，但不会改变吸附/解吸的能量特性。
通过吸附/解吸平衡，包含由各种组分阻碍的表面点位的效应。

过程速率由以下公式给出：
图 54. EQUATION_DISPLAY

$q = k^{'} \frac{\underset{i}{Π} {[X_{i}]}^{l_{i}}}{{(1 + \underset{i}{Σ} K_{i} {[X_{i}]}^{n_{i}})}^{m}}$

(3408)
其中为速率常数，由 Eqn. (3365) 求出，为气相组分的浓度，而为吸附/解吸步骤的平衡常数，由以下公式给出： $k'$ $[X_{i}]$ $i$ $K_{i}$
图 55. EQUATION_DISPLAY

$K_{i} = A_{i} T^{β_{i}} \exp (- H_{i} / R T)$

(3409)
上标指数 $m$ ，当 $m = 2$ 时对应于 Langmuir-Hinshelwood 反应，当 $m = 1$ 时对应于 Eley-Rideal 反应。

颗粒化学

对于颗粒反应，速率常数 $k$ 使用阿雷尼乌斯方程 Eqn. (3365) 确定。由于颗粒化学反应率考虑随动能产生的扩散，因此理论指南的颗粒反应一节介绍了这些计算。