整体沸腾

Simcenter STAR-CCM+ 中的混合多相 (MMP) 整体沸腾对流体内部的沸腾和冷凝建模。

相间质量传递速率仅取决于从液体和蒸汽到这两个相之间的饱和交界面的传热率。按尺寸和数密度明确描述气泡可得出交界面面积密度，这一点很重要。

此热驱动模型不适用于描述既没有气泡（均相成核）或蒸发（浓度驱动的多组分质量传递），也没有空化（惯性有限的质量传递）的沸腾。如果生成的相间质量传递速率出现在比流动时间尺度短得多的时间尺度上，则此模型也不适用。可能无法使用分离求解器算法解决此情景。

从相变交界面到该交界面任一侧上这两个相中的每个相的热传递建模为：

图 1. EQUATION_DISPLAY

Q_{i}^{(i j)} = h_{i}^{(i j)} a_{i j} (T_{i j} - T)

(2909)

Q_{j}^{(i j)} = h_{j}^{(i j)} a_{i j} (T_{i j} - T)

其中：

交界面温度通常定义为特定系统压力的固定饱和温度。在 Simcenter STAR-CCM+ 中，可以选择将场函数用于交界面温度，这样便可将深度考虑在内，即：因微米级气泡中的表面张力引起的超压。

连续相的能量供应热传递系数为：

图 2. EQUATION_DISPLAY

h_{i}^{(i j)} = N u_{i} k_{i} / l_{i j}

(2910)

其中， $N u_{i}$ 为连续相努赛尔数， $l_{i j}$ 为相对的相互作用长度尺度（通常是气泡尺寸）。

同样，对于离散相，能量供应热传递系数为：

图 3. EQUATION_DISPLAY

h_{j}^{(i j)} = N u_{j} k_{j} / l_{i j}

(2911)

其中， $N u_{j}$ 为离散相努赛尔数。

连续相努赛尔数使用 Eqn. (2043)进行计算。由于颗粒内部的对流过程通常定义不佳，因此该相关性不适用于离散相努赛尔数。

在多流态相间相互作用中，整体沸腾/冷凝的典型情景如下所示：

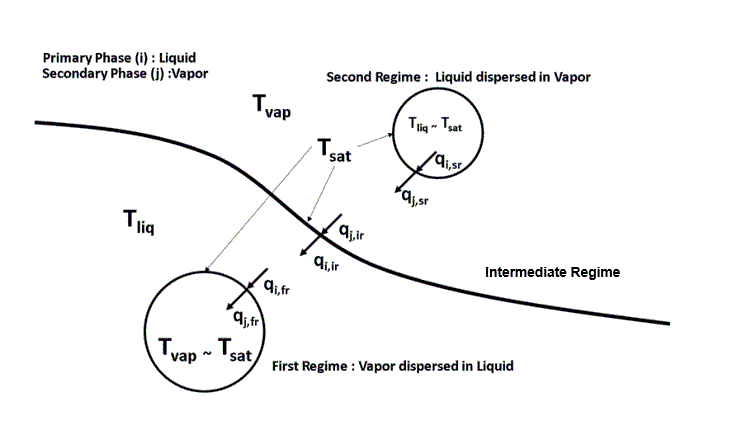
计算了一对主相 ( $i$ ) 和次相 ( $j$ ) 的总共六种情况的热传递。即，对于每个流态，计算了从相到交界面的热传递。来自主相和次相的能量供应热传递系数是第一离散流态、中间流态和第二离散流态的交界面处热传递系数的加权总和：

图 4. EQUATION_DISPLAY

h_{i}^{(i j)} a_{i j} = \sum_{r = f r, i r, s r} W_{r} (h_{i, r}^{(i j)} a_{i j, r})

(2912)

图 5. EQUATION_DISPLAY

h_{j}^{(i j)} a_{i j} = \sum_{r = f r, i r, s r} W_{r} (h_{j, r}^{(i j)} a_{i j, r})

(2913)

在上述方程中，不同区的主侧和次侧热传递系数计算如下：

对于主（液体）侧：
- 第一离散流态， $h_{i, f r} = {N u}_{i, f r} \frac{k_{i}}{l_{f r}}$
- 中间流态 $h_{i, i r} = {N u}_{i, i r} \frac{k_{i}}{l_{i r}}$
- 第二离散流态 $h_{i, s r} = {N u}_{i, s r} \frac{k_{i}}{l_{s r}}$
对于次（蒸汽）侧：
- 第一离散流态， $h_{j, f r} = {N u}_{j, f r} \frac{k_{j}}{l_{f r}}$
- 中间流态 $h_{j, i r} = {N u}_{j, i r} \frac{k_{j}}{l_{i r}}$
- 第二离散流态 $h_{j, s r} = {N u}_{j, s r} \frac{k_{j}}{l_{s r}}$

注	在第一和第二离散流态中，当球体内的高对流不符合预期时，可能会出现一些特定情况。在这些情况下，气泡和液滴可以视为集总体。为确保球体内（即第一离散流态的蒸汽侧和第二离散流态的液体侧）的温度均匀，可通过使用相应的流体属性将努赛尔数计算为 $\frac{h_{i n t e r n a l} \cdot l}{k}$ ，其中， $h_{i n t e r n a l} = \frac{ρ \cdot c p \cdot l}{Δ t_{s}}$ 。 $Δ t_{s}$ 为确保快速达到温度平衡的松弛时间尺度，可以设为较低的值，例如， $Δ t_{s} = 1 e^{- 5} s$ 。

Hughes-Duffey 相关性

中间区中的液体侧热传递系数根据由 Hughes 和 Duffey 的研究 ([478]) 引入的表面更新理论计算。此理论预测的努赛尔数为：

图 6. EQUATION_DISPLAY

{N u}_{i, i r} = \frac{2}{\sqrt{π}} {Re}_{t} \Pr_{i}^{1 / 2}

(2914)

其中：

${Re}_{t} = l_{t} u_{t} / ν_{l}$ 为湍流雷诺数
- $l_{t}$ 为湍流长度比例
- $u_{t}$ 为湍流速度比例
- $ν_{l}$ 为液体运动粘度。
$P_{r l}$ 为液体普朗特数。

仅当主相为湍流模型时，此方法才可用。

交界面质量通量根据热平衡计算得出：

图 7. EQUATION_DISPLAY

m^{(i j)} = - \frac{Q_{i}^{(i j)} + Q_{j}^{(i j)}}{{Δ h}_{i j}}

(2915)

其中：