波剥离

根据流动条件和液膜所在的壁面几何，液膜可能形成液滴，此过程称为液膜剥离。

Simcenter STAR-CCM+ 可以因以下因素对液膜剥离进行建模：

相邻流体和体积力引起的不稳定性

因液膜与其周围流体之间交界面上的外力（例如重力或剪切），液膜表面会产生不稳定性并开始脱落液滴。按照 Hervé Foucart [618]，Simcenter STAR-CCM+ 将液膜剥离建模成一个三阶段过程：

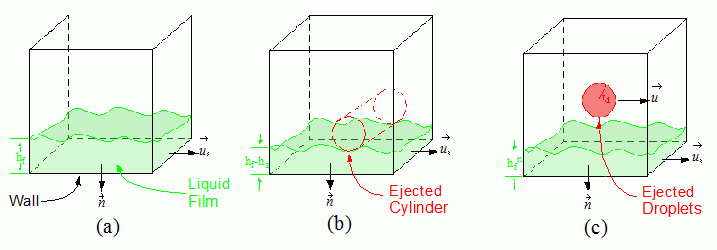
对于表面剥离，该模型假定以下情况：

最不稳定的波长是最可能发生表面破碎的波长。使用耗散方程将此波长计算为共振波长：

图 1. EQUATION_DISPLAY

λ_{res} = \frac{2 π}{ρ_{f} f_{b} \cdot n} (\frac{1}{3} ρ {\tilde{v}}_{r}^{2} - \sqrt{{(\frac{1}{3} ρ {\tilde{v}}_{r}^{2})}^{2} - ρ_{f} f_{b} \cdot n σ})

(2749)

其中， ${\tilde{v}}_{r}^{2}$ 是液膜与周围流体之间的相对速度的平方 $(v_{f} - v) \cdot (v_{f} - v)$ ， $σ$ 是表面张力， $f_{b}$ 是作用在液膜上的体积力（也包括惯性力）。液滴喷射所需的最低液膜高度则为：

图 2. EQUATION_DISPLAY

h_{min} = c_{H} \frac{λ_{res}}{2 π}

(2750)

要剥离的液膜高度（即表面波幅值）为：

图 3. EQUATION_DISPLAY

h_{a} = {[{\frac{3}{4} (\frac{2}{3.78})}^{3}]}^{2} π λ_{res}

(2751)

生成的液滴直径为：

图 4. EQUATION_DISPLAY

D_{d} = c_{D} \sqrt{\frac{λ_{res} h_{a}}{π}}

(2752)

注	对于剥离为离散相的波，不会使用 Eqn. (2752)。液滴直径将手动指定，而不是通过计算得出。

$c_{D}$ 的默认设置为 3.78。Eqn. (2751) 中的数值 3.78 源自瑞利理论。这意味着，从圆柱体生成的每个液滴的直径均为该圆柱体直径的 3.78 倍。

所有液滴最初具有与液膜相同的速度，且放置在网格单元中心和边界面中心之间的点上，具体取决于喷射的液滴半径。

尽管原始剥离模型中没有考虑时间尺度，但能够根据线性增长率将时间尺度定义为：

图 5. EQUATION_DISPLAY

t_{b} = \frac{λ_{res} (ρ_{f} + ρ)}{| v_{r} | \sqrt{(1 - We) ρ_{f} ρ}}

(2753)

其中， $We$ 为韦伯数。在 Eqn. (2753) 中， $We = 2 / 3$ ，这是最不稳定模式下的值。

使用此时间尺度时，时间步 $Δ t$ 期间预期发生 $n_{b}$ 次剥离：

图 6. EQUATION_DISPLAY

n_{b} = c_{B} \frac{Δ t}{t_{b}}

(2754)

波剥离模型需要测量自由流速（Eqn. (2749) 方程中使用的 $v_{r}$ ）。

Simcenter STAR-CCM+ 将计算自由流速的两个度量并使用最高值。

在自由表面上的气体侧，剪切（或摩擦）速度定义为：

图 7. EQUATION_DISPLAY

v_{*} = - \sqrt{\frac{τ}{ρ}} n_{τ}

(2755)

其中， $n_{τ}$ 是剪切应力 $τ$ 方向上的单位矢量。

假设自由流气体速度可以由下式近似计算得出：

图 8. EQUATION_DISPLAY

v_{r} \approx {(v)}_{int} + K_{*, \infty} v_{*} = v

(2756)

其中， ${(v)}_{int}$ 是在交界面处的速度， $K_{*, \infty}$ 是气体速度的比例缩放因子。