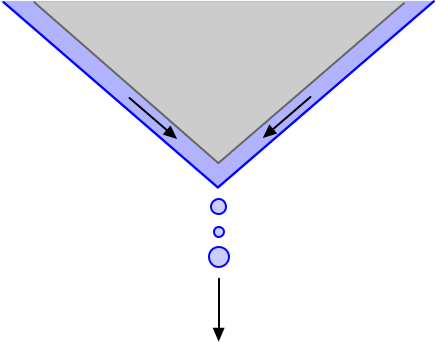
边缘剥离

边缘剥离可对液膜在锐边上的破碎过程建模。

Maroteaux 等人 [626] 针对液膜在锐边上的破碎过程提出了一个模型。此模型基于瑞利-泰勒不稳定性并包含破碎条件和生成的液滴直径分布。但是，Gubaidullin [620] 对破碎条件的有效性提出了疑问。因此，我们采用了 Friedrich 等人 Friedrich 等人 [619] 基于力平衡提出的备选条件。液滴直径分布仍遵循 Maroteaux 理论。

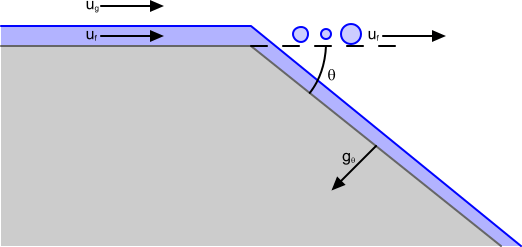
该模型仅应用于棱角（上图中的 $θ$ ）大于用户自定义的最小棱角 $θ_{\min}$ 的边。如果边界面具有多条锐边，所有这些边上会以加权方式发生剥离。

力比 $F R$ （它是液膜动量通量与表面张力和重力之比）如下：

图 1. EQUATION_DISPLAY

F R = \frac{{We}_{f}}{1 + \frac{1}{\sin θ} + {Bo}_{f} \frac{L_{b}}{h_{f} \sin θ}}

(2757)

其中， ${We}_{f}$ 为液膜韦伯数， ${Bo}_{f}$ 为邦德数， $L_{b}$ 为破碎长度， $h_{f}$ 为液膜厚度。

液膜韦伯数如下：

图 2. EQUATION_DISPLAY

{We}_{f} = \frac{ρ_{f} {v_{f}}^{2} h_{f}}{σ}

(2758)

其中， $ρ_{f}$ 为液膜密度， $v_{f}$ 为投影方向与剥离边正交的液膜速度， $h_{f}$ 为液膜厚度， $σ$ 为表面张力。

薄膜邦德数如下：

图 3. EQUATION_DISPLAY

{Bo}_{f} = \frac{ρ_{f} {g_{θ} h}_{f}^{2}}{σ}

(2759)

其中， $g_{θ}$ 为垂直于下游壁面的加速度分量。

Arai 和 Hashimoto [613] 给定破碎长度如下：

图 4. EQUATION_DISPLAY

L_{b} = 0.0388 {h_{f}}^{0.5} {Re}_{f}^{0.6} {We}_{rel}^{- 0.5}

(2760)

其中， ${Re}_{f}$ 为液膜雷诺数， ${We}_{rel}$ 为相对韦伯数。

液膜雷诺数如下：

图 5. EQUATION_DISPLAY

{Re}_{f} = \frac{ρ_{f} v_{f} h_{f}}{μ_{f}}

(2761)

其中， $μ_{f}$ 为动力粘度。

相对韦伯数如下：

图 6. EQUATION_DISPLAY

{We}_{rel} = \frac{h_{f} ρ {(v_{g} - v_{f})}^{2}}{2 σ}

(2762)

其中， $ρ$ 为气体密度， $v_{g}$ 为与剥离边垂直的气体速度分量。

如果 $F R > F R_{C}$ ，其中 ${F R}_{C}$ 为用户自定义的临界力比（在 [619] 中提出），则可视为发生破碎。临界力比的默认值为 1。在经过该边的流体中，只有小部分 $x_{S}$ 与液膜分离。使用以下公式对此分数求近似值：

图 7. EQUATION_DISPLAY

x_{S} = {\begin{matrix} 0 & if F R \leq F R_{C} \\ 0.44 (F R - F R_{C}) & if F R_{c} < F R \leq (F R_{C} + 1.6) \\ 0.057 (F R - F R_{C} - 1.6) + 0.704 & if (F R_{C} + 1.6) < F R \leq ({F R}_{c} + 6.792) \\ 1 & if ({F R}_{C} + 6.792) < F R \end{matrix}

(2763)

基于 [619] 中的实验数据。

注	对于进入离散相的边缘剥离，不会使用 Eqn. (2764) 到 Eqn. (2769)。液滴直径将手动指定，而不是通过计算得出。

对于液滴形成，采用 [626] 中提出的模型估计父液滴直径 $D_{d}$ ，如下所示：

图 8. EQUATION_DISPLAY

D_{d} = c_{1} \sqrt{\frac{λ h_{f}}{π}}

(2764)

其中， $c_{1}$ 为用户自定义的液滴直径比例因子。默认情况下，该因子设为 3.78。根据最不稳定波数 $k$ 计算波长 $λ$ ，这将最大化增长率：

图 9. EQUATION_DISPLAY

ω = - (\frac{σ - (ρ_{f} - ρ) a / k^{2}}{2 μ_{f} h_{f}}) (\frac{(k h_{f}) \sinh (k h_{f}) \cosh (k h_{f}) - k^{2} h_{f}^{2}}{\cosh^{2} (k h_{f}) + k^{2} h_{f}^{2}})

(2765)

其中，加速度 $a$ 的计算方法如下：

图 10. EQUATION_DISPLAY

a = \frac{v_{f}^{2} θ}{h_{f} (π + θ)}

(2766)

$λ$ 与 $k$ 的关系为 $λ = 2 π / k$ 。

根据该模型，累积液滴大小分布 $F (D)$ 是 Rosin-Rammler 分布：

图 11. EQUATION_DISPLAY

F (D) = 1 - e^{- {(D / X)}^{q}}

(2767)

其中， $q$ 为用户自定义的参数，默认设为 1.5，并且：

图 12. EQUATION_DISPLAY

X = \frac{D_{d}}{{(3 \ln 10)}^{1 / q}}

(2768)

有两个选项用于确定液滴直径：

使用确定性直径（计算为尺寸分布平均值）生成液滴，如下所示：

图 13. EQUATION_DISPLAY

D = X Γ (1 + \frac{1}{q})

(2769)

其中， $Γ (x)$ 表示 Gamma 函数。

根据 Eqn. (2767) 使用随机化直径 $D$ 生成液滴。

液滴以液膜速度喷射。

从两侧的流体剥离边缘

如果流体从两侧向一边靠近，则流体将合并成一串符合质量、动量、组分和能量守恒定律的拉格朗日液滴。例如，如果两个流体具有不同的温度，液滴温度设为介于两者之间的值。对于异向流体，两侧的剥离分数 $x_{S}$ (Eqn. (2763)) 设为 1（表示完全剥离）。液滴直径根据通量最高一侧的薄膜属性计算得出。下图说明了异向流体的边缘剥离。