接触力

DEM 中的接触力公式通常是弹簧-阻尼器模型的一种变体。弹簧产生排斥力将颗粒推开，而阻尼器表示粘性阻尼并允许模拟除完全弹性以外的碰撞类型。

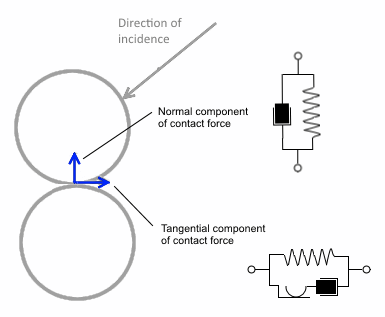
接触点上的力建模为一对弹簧-阻尼器振荡器。并行线性弹簧-阻尼器模型表示法向力，用滑块串联的并行线性弹簧-阻尼器表示力的切向（相对接触平面法向矢量）。在这两者中，弹簧考虑响应的弹性部分，而阻尼器则考虑碰撞期间的能量耗散。

Simcenter STAR-CCM+ 提供了三种接触模型：

Hertz Mindlin
线性弹簧
沃尔顿布劳恩

Hertz-Mindlin 无滑移接触模型

Hertz-Mindlin 接触模型是非线性弹簧-阻尼器接触模型（基于 Hertz-Mindlin 接触理论 [726]、[722]）的一种变体。A 和 B 这两个球体之间的力由以下方程组表示：

图 1. EQUATION_DISPLAY

F_{contact} = F_{n} n + F_{t} t

(3250)

其中， $F_{n}$ 和 $F_{t}$ 分别为法向和切向分量的幅值。

法向由以下各项定义：

法向力：
图 2. EQUATION_DISPLAY

$F_{n} = {- K}_{n} d_{n} - N_{n} v_{n}$

(3251)
法向弹簧刚度：
图 3. EQUATION_DISPLAY

$K_{n} = \frac{4}{3} E_{e q} \sqrt{d_{n} R_{e q}}$

(3252)
法向阻尼：
图 4. EQUATION_DISPLAY

$N_{n} = \sqrt{({5 K}_{n} M_{e q})} N_{n damp}$

(3253)

其中， $N_{n damp}$ 为法向阻尼系数，如 Eqn. (3257) 中给定。

切向由以下各项定义：

如果 $| K_{t} d_{t} | < | K_{n} d_{n} | C_{f s}$ ，其中， $C_{f s}$ 为静摩擦系数，则切向力由 $- K_{t} d_{t} - N_{t} v_{t}$ 定义。否则：
图 5. EQUATION_DISPLAY

$F_{t} = \frac{| K_{n} d_{n} | C_{f s} d_{t}}{| d_{t} |}$

(3254)
切向弹簧刚度：
图 6. EQUATION_DISPLAY

$K_{t} = 8 G_{e q} \sqrt{d_{n} R_{e q}}$

(3255)
切向阻尼：
图 7. EQUATION_DISPLAY

$N_{t} = \sqrt{({5 K}_{t} M_{e q})} N_{t damp}$

(3256)

其中， $N_{t damp}$ 为切向阻尼系数，如 Eqn. (3258) 中给定。

图 8. EQUATION_DISPLAY

N_{n damp} = \frac{- ln (C_{n rest})}{\sqrt{π^{2} + {\ln (C_{n rest})}^{2}}}

(3257)

图 9. EQUATION_DISPLAY

N_{t damp} = \frac{- ln (C_{t rest})}{\sqrt{π^{2} + {\ln (C_{t rest})}^{2}}}

(3258)

此处， $C_{n rest}$ 和 $C_{t rest}$ 为法向和切向恢复系数，属于用户设置的模型参数。如果 $C_{n rest} = 0$ ，则 $N_{n damp} = 1$ ；如果 $C_{t rest} = 0$ ，则 $N_{t damp} = 1$ 。

等效半径定义为：

图 10. EQUATION_DISPLAY

R_{e q} = \frac{1}{\frac{1}{R_{A}} + \frac{1}{R_{B}}}

(3259)

等效颗粒质量为：

图 11. EQUATION_DISPLAY

M_{e q} = \frac{1}{\frac{1}{M_{A}} + \frac{1}{M_{B}}}

(3260)

等效杨氏模量表示为：

图 12. EQUATION_DISPLAY

E_{e q} = \frac{1}{\frac{1 - ν_{A}^{2}}{E_{A}} + \frac{1 - ν_{B}^{2}}{E_{B}}}

(3261)

等效剪切模量为：

图 13. EQUATION_DISPLAY

G_{e q} = \frac{1}{\frac{2 (2 - ν_{A}) (1 + ν_{A})}{E_{A}} + \frac{2 (2 - ν_{B}) (1 + ν_{B})}{E_{B}}}

(3262)

其中：

$M_{A}$ 和 $M_{B}$ 为球体 A 和 B 的质量。
$d_{n}$ 和 $d_{t}$ 为接触点处的法向和切向重叠。
$R_{A}$ 和 $R_{B}$ 为球体的半径。
$E_{A}$ 和 $E_{B}$ 为球体的杨氏模量。
$ν_{A}$ 和 $ν_{B}$ 为泊松比。
$ν_{n}$ 和 $ν_{t}$ 为接触点处相对球体表面速度的法向和切向速度分量。

对于颗粒-壁面碰撞，这些公式保持不变，但假设壁面半径和质量为 $R_{w a l l} = \infty$ 和 $M_{w a l l} = \infty$ ，因此等效半径减少至 $R_{e q} = R_{p a r t i c l e}$ ，等效质量减少至 $M_{w a l l} = M_{p a r t i c l e}$ 。

Di Renzo 和 Di Maio [722] 针对切向微滑移和切向力计算的细节处理提出了几个公式。Simcenter STAR-CCM+ 使用 Tsuji 提出的公式 [737]，其中假设切向力为非线性，但细节微滑移追踪由解析表达式替换。生成的代码计算效率较高，且仍与实验数据匹配。

临界速度: 当颗粒壁面冲击速度超过临界速度时，颗粒有足够的能量穿过壁面边界。Simcenter STAR-CCM+ 计算临界速度的方程如下：
图 14. EQUATION_DISPLAY

$v_{crit} = \sqrt{\frac{4}{5} \frac{E}{π ρ (1 - ν^{2})}}$

(3263)
其中 $E$ 为杨氏模量， $ρ$ 为密度， $ν$ 为泊松比。

线性弹簧接触模型

该模型基于 Cundall 和 Strack 的成果 [720]。法向力和切向力 $F_{n}$ 和 $F_{t}$ 如 Eqn. (3251) 和 Eqn. (3254) 中所定义，但是参数 $K_{n}$ 、 $K_{t}$ 、 $N_{n}$ 和 $N_{t}$ 的定义如下：

$K_{n}$ 为法向弹簧常数。
$K_{t}$ 为切向弹簧常数。
$N_{n} = 2 N_{n d a m p} \sqrt{K_{n} M_{e q}}$ 其中：
- $N_{n d a m p}$ 为法向阻尼系数，如 Eqn. (3257) 中所示。
- $M_{e q}$ 为等效颗粒质量，如 Eqn. (3260) 中所示。
$N_{t} = 2 N_{t d a m p} \sqrt{K_{t} M_{e q}}$ 其中， $N_{t d a m p}$ 为切向阻尼系数，如 Eqn. (3258) 中所示。

当线性弹簧模型使用基于颗粒材料方法时，基于线性模型是线性化 Hertz 模型的假设估计弹簧刚度，其中最大法向接触力为：

图 15. EQUATION_DISPLAY

K_{n} δ_{\max} = \frac{4}{3} E_{e q} \sqrt{R_{e q} δ_{\max}} δ_{\max}

(3264)

其中：

$δ_{\max}$ 为最大重叠。
$E_{e q}$ 为 Eqn. (3261) 中定义的等效杨氏模量。
$R_{e q}$ 为 Eqn. (3259) 中定义的等效半径。

要计算弹簧常数，假设：

图 16. EQUATION_DISPLAY

λ_{\max} = \frac{δ_{\max}}{R_{e q}}

(3265)

由此得出法向弹簧常数 $K_{n}$ 为：

图 17. EQUATION_DISPLAY

K_{n} = \frac{4}{3} \sqrt{λ_{\max}} E_{e q} R_{e q}

(3266)

切向弹簧常数 $K_{t}$ 为：

图 18. EQUATION_DISPLAY

K_{t} = 8 \sqrt{λ_{\max}} G_{e q} R_{e q}

(3267)

其中， $G_{e q}$ 为等效剪切模量，如 Eqn. (3262) 中定义。

沃尔顿布劳恩迟滞接触模型

沃尔顿布劳恩迟滞塑料弹性接触系统具有以下关系：

图 19. EQUATION_DISPLAY

F_{n} = {- K}_{1} δ n

(3268)

加载接触时，以及：

图 20. EQUATION_DISPLAY

F_{n} = {- K}_{2} (δ - δ_{deformation}) n

(3269)

卸载期间，其中：

图 21. EQUATION_DISPLAY

K_{1} = 1.6 π R Y_{0}

(3270)

图 22. EQUATION_DISPLAY

K_{2} = \frac{1}{E_{f}} K_{1}

(3271)

图 23. EQUATION_DISPLAY

Y_{0} = E \cdot YieldStressFraction

(3272)

图 24. EQUATION_DISPLAY

δ_{deformation} = δ_{max} (1 - E_{f})

(3273)

$E$ 为材料杨氏模量， $δ$ 为接触法向重叠， $n$ 为接触法向矢量，屈服应力分数是一个用户可控模型属性，用于定义塑性变形的开始。 $E_{f}$ 是一个用户可控能量分数，用于定义卸载期间恢复的能量， $δ_{max}$ 为接触加载期间达到的最大重叠。

接触循环

形成颗粒接触后，将在每个时间步追踪接触状态，如下所示：

如果 $v_{r} \cdot n \geq 0$ 且 $δ > δ_{max}$ ，其中， $v_{r}$ 为相对表面速度，则接触视为加载。
加载接触时，使用 $K_{1}$ 刚度计算力，并将 $δ_{max}$ 更新为 $δ$ 的值。
如果不加载接触，则为卸载 ( $v_{r} \cdot n < 0$ ) 或重新加载 ( $δ \leq δ_{max}$ )。卸载期间，使用 $K_{2}$ 刚度计算法向力，但不更新 $δ_{max}$ 的值。
如果颗粒完全分离，则移除颗粒追踪信息并将后续接触视为新接触。

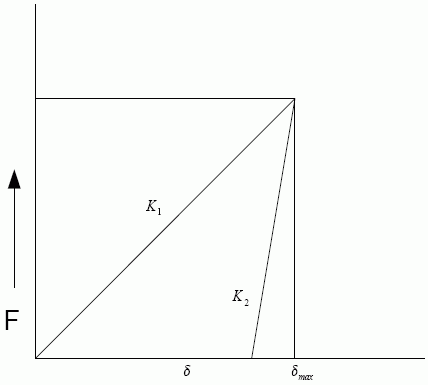
几何解释

加载/卸载循环的几何表示如下：