Particle Clustering and Breakup

Particle bonding is used to extend the particle model to more complex (compliant) shapes or structures. You use the particle clumps model to create groups of particles that represent a complex shape. The particle clumps model invokes the bonded particles model where the individual particles retain their separate identities and are linked by elastically compliant bonds, to each other or to a wall. The addition of a damage model allows the fracture and fragmentation of the clump with the constituent particles separating from the clump.

The composite particle model, on the other hand, treats the ensemble as a single rigid body that does not separate during the simulation.

Particle agglomeration use the same mechanism as the clumped particles, however the bonds are formed in an interval during the simulation as particles collide or according to a user-given criterion. This forming of bonds can be part of an initialization phase where, for example, particles are packed into a volume and an initial configuration is formed. The mechanism is also used to represent a process, for example, a tableting process during the simulation. The result is to form a compliant structure with damage as an option.

Particle Bonding Model

The particle bonding model is used by both the particle agglomeration model and the bonded particle (clumps) model. The particle agglomeration model uses particle bonding to describe interactions between the constituent particles, but also models elastic collisions between particles, based on the elastic contact models chosen by the user. The bonded particle (clumps) model uses only the particle bonding model.

The particle bonding model simulates cumulative damage to bonds. When an interaction producing some damage but falls short of failure, the amount of that damage is reflected in the reduced strength of the bond.

The parallel bond forces are represented in the following governing equations [730].

Force and torque on a particle due to parallel bonds is:

图 1. EQUATION_DISPLAY

F_{i} = F_{n} n_{i} + F_{s} t_{i}

(3279)

图 2. EQUATION_DISPLAY

M_{i} = M_{n} n_{i} + M_{s} t_{i}

(3280)

where the terms $F_{n}, M_{n}$ denote the normal and $F_{s}, M_{s}$ denote the shear components of forces and torques with respect to the contact plane, and:

图 3. EQUATION_DISPLAY

{Δ F}_{n} = k_{n} A {Δ U}_{n}

(3281)

图 4. EQUATION_DISPLAY

{Δ F}_{s} = - k_{s} A {Δ U}_{s}

(3282)

图 5. EQUATION_DISPLAY

Δ M_{n} = - k_{s} J {Δ Ω}_{n}

(3283)

图 6. EQUATION_DISPLAY

Δ M_{s} = - k_{n} I {Δ Ω}_{s}

(3284)

where:

图 7. EQUATION_DISPLAY

A = π R^{2}

(3285)

图 8. EQUATION_DISPLAY

I = \frac{1}{4} π R^{4}

(3286)

图 9. EQUATION_DISPLAY

J = \frac{1}{2} π R^{4}

(3287)

图 10. EQUATION_DISPLAY

k_{n} = \frac{E_{e q}}{R_{a} + R_{b}}

(3288)

图 11. EQUATION_DISPLAY

k_{s} = 6 (\frac{G_{e q}}{R_{a} + R_{b}})

(3289)

图 12. EQUATION_DISPLAY

Δ U = V_{relative} Δ t

(3290)

where $Δ U_{n}$ is the normal component of $Δ U$ , and $Δ U_{s}$ is the tangential component of $Δ U$ .

图 13. EQUATION_DISPLAY

Δ Ω = ω_{relative} Δ t

(3291)

where $Δ Ω_{n}$ is the normal component of $Δ Ω$ , and $Δ Ω_{s}$ is the tangential component of $Δ Ω$ .

The parallel bond can be treated as brittle and disintegrative when shear and tensile stresses exceed prescribed limit values. The stress limit values are calculated based on beam theory to be:

图 14. EQUATION_DISPLAY

δ_{m} = \frac{- F_{n}}{A} + \frac{| M_{s} | R}{I}

(3292)

图 15. EQUATION_DISPLAY

σ_{m} = \frac{| F_{s} |}{A} + \frac{| M_{n} | R}{J}

(3293)

where:


$δ_{m}$	maximum tensile stress that is calculated in the bond
$σ_{m}$	maximum shear stress that is calculated in the bond

If either value exceeds the predefined maximum, the bond is removed and the forces are further calculated only based on the granular interaction of particles.

Simple Failure Model

The simple failure model breaks a bond in the simulation if tensile stress or shear stress on the bond exceed one of the user-specified maximum values $δ_{max}$ and $σ_{max}$ .

The bond fails if:

δ_{m} > δ_{\max} or σ_{m} > σ_{\max}

where:

$δ_{\max}$ is the maximum tensile stress that is allowed without failure of the bond .
$σ_{\max}$ is the maximum shear stress that is allowed without failure of the bond .

Impact Cutting Model

The impact cutting model breaks a bond in the simulation if the particle impact velocity magnitude $v_{imp}$ exceeds the user-specified Impact Velocity Threshold $v_{thr}$ , where $v_{imp}$ is the magnitude of the relative velocity between the particle and the wall at the contact point. The model applies to fiber particles and particle clumps.

For a particle with multiple bonds, only one bond can break at a time if more than one fiber segment or pair of clumped spheres satisfies the breakage criterion. In this situation, the breaking bond is the one closest to the impact position. For the two end segments, only one bond exists though.

Secondary breakage can occur after the time from the previous breakage exceeds the user-specified Breakage Time Interval.

The model determines which bond breaks using the following steps:

Identify the segment with the maximum impact velocity magnitude that exceeds $v_{thr}$ : $v_{i} = v_{max} \geq v_{thr}$
with:
$v_{max} = max {v_{i}}, i = 1, \dots, N$
where:
- $v_{max}$ is the maximum impact velocity magnitude among all segments of a fiber or spheres of a clumped particle.
- $N$ is the number of bonded components of a bonded particle.
For secondary breakage, check if $t - t_{b} \geq Δ t$
where:
- $t_{b}$ is the time of the previous breakage.
- $Δ t$ is the user-specified Breakage Time Interval.
Let $j$ and $k$ be the two bonds associated with the segment, $x_{j}$ and $x_{k}$ be their bond locations, and $x_{c}$ be the impact position. Then the bond to break is $j$ if $| x_{j} - x_{c} | < | x_{k} - x_{c} |$ , or $k$ otherwise.

Constant Rate Damage Model

The constant rate damage model simulates the weakening and breaking of bonds between particles in a clump due to collisions.

The constant rate damage model follows the stress-strain curve shown in the following figure:

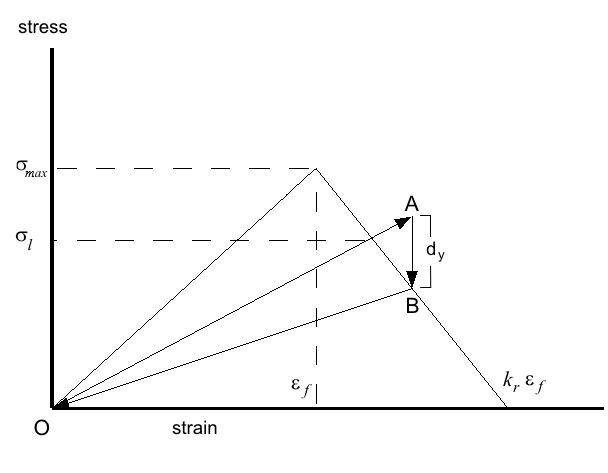
The point ( $ε_{f}$ , $σ_{max}$ ) is the point of strain $ε_{f}$ at failure and maximum stress $σ_{max}$ induced by that strain. Once conditions reach the point ( $ε_{f}$ , $σ_{max}$ ), the model calculates the damage required to return the stress to the failure surface, defined by the line from ( $ε_{f}$ , $σ_{max}$ ) to ( $k_{r} ε_{f}$ , 0), where $k_{r}$ is the fracture softening modulus, a model parameter with default value 2 at constant strain. For stability, $k_{r}$ should be greater than 1. [727]

If $d_{i}$ is the damage at time-step $i$ , the damage at time-step $i + 1$ is:

图 16. EQUATION_DISPLAY

d_{i + 1} = \min (d_{y}, d_{v}, 1)

(3294)

where:

$d_{v}$ is the amount of damage produced by the fastest possible speed of crack growth:

图 17. EQUATION_DISPLAY

d_{v} = d_{i} + 2 \sqrt{d_{i}} \frac{C_{r}}{r_{b}} Δ t + {(\frac{C_{r}}{r_{b}})}^{2} Δ t^{2}

(3295)

$C_{r}$ is the Rayleigh wave speed.
$r_{b}$ is the bond radius.
$Δ t$ is the size of the time-step.

图 18. EQUATION_DISPLAY

d_{y} = \frac{k_{r}}{k_{r} - 1} (1 - (1 - d_{i}) \frac{σ_{m}}{σ_{o}})

(3296)

where:


$k_{r}$	fracture softening modulus, a model parameter, default value 2
$σ_{max}$	maximum shear stress that is allowed without failure of the bond, determined by the Tensile Strength Method property of the Constant Rate Damage model
$σ_{o}$	maximum tensile stress for the bond [718], [736]

The maximum tensile stress for the bond is calculated as:

图 19. EQUATION_DISPLAY

σ_{o} = \sqrt{\max {(0, δ_{m})}^{2} + σ_{m}}

(3297)

where:

$δ_{m}$ is the calculated value of the locally maximum tensile stress within the bond. See Eqn. (3292).
$σ_{m}$ is the calculated value of the locally maximum shear stress within the bond. See Eqn. (3293).

If $σ_{o} > σ_{l}$ , damage is evolving:

图 20. EQUATION_DISPLAY

σ_{l} = σ_{max} \frac{k_{r} (1 - d_{i})}{(k_{r} - 1) (1 - d_{i}) + 1}

(3298)

As a bond is damaged, its stiffness is modified. When the bond is in tension, the stiffness of the bond, which is represented by the parameters $k_{n}$ and $k_{s}$ in Eqn. (3282) to Eqn. (3284), is reduced by a multiplicative factor. This multiplicative factor is $(1 - d_{i})$ . The factor represents the reduced area that remains intact in the damaged bond.

When the bond is in compression, no reduction of stiffness occurs, because the direct contact of a fracture surface transmits the normal load. The resultant friction together with surface asperities work to transmit the shear force.