参与介质辐射

Simcenter STAR-CCM+ 使用离散坐标法 (DOM) 或球体谐波来考虑参与介质影响。

DOM 是一种数值模型，用于描述参与介质中的辐射热传递。它模拟形成闭合集合的漫射/反射表面之间的热辐射交换。

球体谐波模型模拟热辐射各向异性传播，传播模式以球体谐波函数表示。它不模拟折射或镜面反射。

表面辐射属性使用发射率、镜面和漫射反射率、透射率和辐射温度进行量化。这些属性与方向无关。对于多波段光谱模型，表面属性可以与波长相关。

填充表面间空间的介质还可以吸收、发射或散射辐射。因此，每个表面接收和发射的辐射量取决于此效应，以及表面的光学属性和表面上施加的热边界条件。

随着辐射穿过介质，中间材料在 $Ω$ 方向上吸收并增加其辐射强度 $I$ 。辐射传递方程 (RTE) 控制此过程。此方程可根据特定波长 $λ$ 的辐射强度来编写：

图 1. EQUATION_DISPLAY

\frac{d I_{λ}}{d s} = - β_{λ} I_{λ} + k_{a λ} I_{b λ} + \frac{k_{s λ}}{4 π} \int_{4 π}^{} I_{λ} Ω d Ω + k_{p a λ} I_{p b λ} + \frac{k_{p s λ}}{4 π} \int_{4 π}^{} I_{λ} Ω d Ω

(1721)

其中：


$I_{λ}$	波长 $λ$ [ $W / (m^{2} s r m^{- 1})$ ] 的辐射强度
$I_{b λ}$	波长 $λ$ 的黑体强度
$I_{p b λ}$	波长 $λ$ 的颗粒黑体强度和当前颗粒温度。
$s$	$Ω$ 方向上的距离
$β_{λ}$	熄灭系数，定义如下 $β_{λ} = k_{a λ} + k_{s λ} + k_{p a λ} + k_{p s λ}$
$k_{a λ}$	波长 $λ$ $(m^{- 1})$ 的吸收系数
$k_{s λ}$	波长 $λ$ $(m^{- 1})$ 的散射系数
$k_{p a λ}$	波长 $λ$ $(m^{- 1})$ 的颗粒吸收系数
$k_{p s λ}$	波长 $λ$ $(m^{- 1})$ 的颗粒散射系数
$Ω$	立体角

黑体强度由以下公式给出：

图 2. EQUATION_DISPLAY

I_{b λ} = \frac{2 C_{1}}{λ^{5} (e^{C_{2} / λ T} - 1)}

(1722)

其中， $C_{1} = 0.595522 \times 10^{- 16}$ $W m^{2} / s$ ， $C_{2} = 0.01439$ $m K$ 。

假设内散射组分各向同性。

当介质具有多个组分时，吸收系数 $k_{a λ}$ 由以下公式给出：

图 3. EQUATION_DISPLAY

k_{a λ} = \sum_{i}^{} k_{a λ i}

(1723)

其中， $i$ 为参与组分（如 CO₂、H₂O 或碳烟）的顺序编号。

当介质的吸收系数和散射系数与波长无关时，介质称为灰体。在这种情况下，可按波长（或者，等同于波数）求 RTE 的积分，以生成与波长无关的方程。

颗粒辐射对于连续介质的灰体和多波段辐射均有效。但是，对于多波段（光谱）辐射，颗粒属性仍为灰体。表面和连续体属性可以为光谱，但颗粒属性为灰体（吸收效率与波长无关）。颗粒散射各向同性。

边界条件：反射、折射和辐射

应用于每个波长 $λ$ 的 RTE 的边界条件如下：

图 4. EQUATION_DISPLAY

I_{λ} (s) = ε_{w λ} I_{b λ} + \frac{E_{w λ}^{d}}{π} + \frac{ρ_{w λ}^{d}}{π_{e f f}} \int_{(n \cdot s^{'} < 0)}^{} I_{λ} (s') | n \cdot s^{'} | d Ω + ρ_{w λ}^{s} I_{λ} (s^{s}) + τ_{w λ} (s^{i}) I_{λ} (s^{i})

(1724)

其中：

$ε_{w λ}$ 为漫射发射率
$\frac{E_{w λ}^{d}}{π}$ 为漫射非普朗克发射项
$ρ_{w λ}^{d}$ 为漫射反射率
$π_{e f f} = \sum_{s_{i} \cdot n_{i}} w_{i} (s_{i} \cdot n_{i})$ 为选定坐标集合的半矩
$ρ_{w λ}^{s}$ 为镜面反射率
$s'$ 为沿离开边界的距离坐标的单位矢量
$s^{s} = s - 2 (s \cdot n) n$ 为由反射定律确定的入射光线方向
$s^{i}$ 为由折射定律或斯涅尔定律确定的入射光线方向
$n$ 为表面法向
$τ_{w λ}$ 为透射率。只有交界面可以是部分透射，其他所有外部边界均以不透明的形式建模

$w$ 下标指示边界处的状态。表面法向指向表面。对于折射，边界处的镜面反射率和透射率等辐射属性变为与方向相关。

边界辐射度如下：

J_{w} = \int_{n \cdot s < 0} ϵ_{w} I_{b w} | n \cdot s | d Ω + \int_{n \cdot s > 0} ρ_{w}^{d} (s^{'}) I (s') | n \cdot s^{'} | d Ω + \int_{n \cdot s^{s} > 0} ρ_{w}^{s} (s^{s}) I (s^{s}) | n \cdot s^{s} | d Ω

(1725)

其中：

$I_{b w}$ 为边界处的光谱积分黑体总强度。
$ρ_{w}^{d}$ 和 $ρ_{w}^{s}$ 为边界处的漫射反射率和镜面反射率。

外部边界上的边界辐射度不包括从环境透射而产生的效应。但是，对于交界面边界，辐射度包括从相邻区域透射而产生的效应。这样做是为了使 DOM 与 S2S 保持一致。对于 DOM，辐射度是一个后处理参数。

辐射热通量

特定方向上的辐射热通量 $q_{r}$ 使用辐射强度对所有立体角以及对波长光谱的积分来计算：

图 5. EQUATION_DISPLAY

q_{r} (r) = \int_{0}^{\infty} \int_{4 π} I_{λ} (s) s d Ω d λ

(1726)

辐射求解通过辐射热通量的发散耦合至流体动力学求解。此项在流体与辐射能量场之间交换能量。给定强度场，热通量的发散计算如下：

图 6. EQUATION_DISPLAY

\nabla \cdot {\dot{q}}_{r} = \int_{0}^{\infty} k_{a λ} (4 π I_{b λ} - \int_{4 π}^{} I_{λ} d Ω) d λ

(1727)

折射率和黑体强度

局部黑体强度 $I_{b}$ 按绝对折射率 $n$ 的平方增大：

I_{b} = \frac{n^{2} σ T^{4}}{π}

(1728)

在介质内和边界处，此方程均适用。在介质中，黑体强度乘以吸收系数，而在边界处，则乘以边界发射率。

当辐射从一个介质透射或折射到另一个介质时，强度按以下公式发生变化：

\frac{I_{2}}{n_{2}^{2}} = \frac{I_{1} τ_{1}}{n_{1}^{2}}

其中，下标 $1$ 指示边界的射入端的值，下标 $2$ 指示射出端的值。强度的增大并不违反由普朗克定律给出的发射最大值。只有局部强度增大，而不是整个介质的全局强度增大。

折射、反射和临界角

考虑一下两个连续体之间的交界面边界，两个连续体的折射率分别为 $n_{1}$ 和 $n_{2}$ ，一条光线从第一个连续体传播到第二个连续体。有两种可能的情况：

第 1 种情况：光线从折射率较低的连续体传播到折射率较高的连续体， $n_{2} > n_{1}$
第 2 种情况：光线从折射率较高的连续体传播到折射率较低的连续体， $n_{2} < n_{1}$

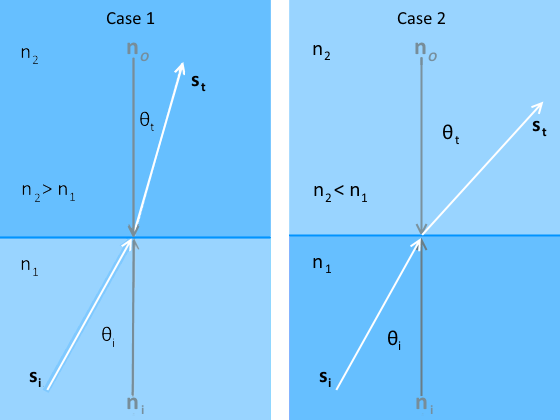
$n_{i}$ 和 $n_{o}$ 是内部和外部单位法向矢量
$s_{i}$ 和 $s_{t}$ 是入射和透射光线的单位方向矢量
$θ_{i}$ 和 $θ_{t}$ 为入射和透射的角度

按照斯涅尔定律，这些角度与折射率相关：

n_{1} \sin (θ_{i}) = n_{2} \sin (θ_{t})

在第 1 种情况下，透射光线在外侧靠近法线，所以所有入射光线都穿透表面。

在第 2 种情况下，透射光线在外侧远离法线。随着 $θ_{i}$ 不断增大， $θ_{t}$ 最终与法线成 90° 而与表面平行。超过这一点，光线反射回第一个介质。发生这种变化时所在的角度称为“临界角” $θ_{c}$ 。

θ_{c} = \sin^{-1} (\frac{n_{2}}{n_{1}})

(1729)

为了运行时的临界角检查而计算和存储的参数如下：

\cos^{2} (θ_{c}) = 1 - {(\frac{n_{2}}{n_{1}})}^{2}

对于第 1 种情况，因为 $n_{2} > n_{1}$ ，所以此方程的右侧为负，这意味着没有临界角和内反射。

对于第 2 种情况，因为 $n_{2} < n_{1}$ ，所以此方程的右侧介于 0 和 1 之间，这意味着存在临界角和内反射。

入射和透射光线的矢量相关，如下所示：

图 7. EQUATION_DISPLAY

s_{t} = \frac{n_{1}}{n_{2}} (s_{i} - (s_{i} \cdot n_{i}) n_{i}) - \sqrt{1 - \sin^{2} (θ_{t})} n_{o}

(1730)

其中：

\sin^{2} (θ_{t}) = {(\frac{n_{1}}{n_{2}})}^{2} (1 - {(s_{i} \cdot n_{i})}^{2})

反射和折射的校正因子

由于按照反射和折射定律计算的射出方向并不总是与预设纵坐标方向对齐，因此 Simcenter STAR-CCM+ 使用最近邻纵坐标方向。此建模在射出能量的方向上产生轻微的偏差，这需要一个校正因子来使该边界面上对半球积分的总能量守恒。

镜面反射的校正因子如下：

图 8. EQUATION_DISPLAY

f^{r e f l} = \frac{\int_{n \cdot s > 0} ρ_{w}^{s} (s^{i}) I (s^{i}) | n \cdot s | d Ω}{\int_{n \cdot s < 0} ρ_{w}^{s} (s_{q u a d}^{i}) I (s_{q u a d}^{i}) | n \cdot s | d Ω}

(1731)

其中：

$ρ_{w}^{s}$ 为镜面反射率。对于没有折射的边界，这是一个空间上和方向上的常数，不参与积分
$s^{i}$ 为射入方向
$s_{q u a d}^{i}$ 为与每个射出正交方向相关的射入方向，使用反射和最近邻正交定律求出

对于有折射的半透明边界，镜面反射率在半球上并不总是常数。如果临界角 $θ_{c}$ 小于 90°，则该入射圆锥外部的镜面反射率等于内部的镜面反射率加上透射率，即 $ρ_{w}^{s} + τ_{w}$ 。

折射透射的校正因子如下：

图 9. EQUATION_DISPLAY

f^{refrac} = \frac{\int_{n \cdot s > 0} τ_{w} (s^{r}) I (s^{r}) | n_{1} \cdot s^{r} | d Ω}{\int {}_{n \cdot s < o}{τ_{w} (s_{q u a d}^{r}) I (s_{q u a d}^{r}) | n_{2} \cdot s |} d Ω}

(1732)

其中：

$s^{r}$ 为透射的射入方向
$s_{q u a d}^{r}$ 为与每个射出正交方向相关的透射射入方向，使用反射和最近邻正交定律求出

要求出 $s_{q u a d}^{r}$ ，首先使用以下公式计算理论入射光线 $i$ ：

i = \frac{n_{2}}{n_{1}} (s_{t} - (s_{t} \cdot n_{o}) n_{o}) - \sqrt{1 - \sin^{2} (θ_{t})} n_{i}

且

\sin^{2} (θ_{i}) = {(\frac{n_{2}}{n_{1}})}^{2} (1 - {(s_{t} \cdot n_{o})}^{2})

随后，使用此理论入射光线 $i$ 求出临界角 $θ_{c}$ 以内的最近正交方向。

对于透射率 $τ_{w}$ ，如果临界角 $θ_{c}$ 小于 90°，则入射圆锥外部的透射率为零。

随后，射出强度由 Eqn. (1724) 给出，包括 DOM 方向校正：

图 10. EQUATION_DISPLAY

I_{λ} (s) = ε_{w λ} I_{b λ} + \frac{ρ_{w λ}^{d}}{π_{e f f}} \int_{n \cdot s' < 0} I_{λ} (s') | n \cdot s^{'} | d Ω + f^{refl} ρ_{w λ}^{s} (s_{q u a d}^{i}) I_{λ} (s_{q u a d}^{i}) + f^{refrac} τ_{w λ} (s_{q u a d}^{i}) I_{λ} (s_{q u a d}^{r})

(1733)

全光谱 k 分布公式

K-分布热辐射模型用于对参与介质中的 H₂O 和 CO₂ 光谱变化建模。选择该模型后，基于重新排序的光谱求解辐射传递方程 (RTE)。请参见 Modest [411]。相关 k 分布法介绍如何计算吸收系数值以及它们表示的含义。然后，全光谱公式在每个光谱位置上应用这些系数，以得到光谱积分的总辐射热通量：

图 11. EQUATION_DISPLAY

\frac{d I_{k}}{d s} = k f (T, k) I_{b} + k_{p a} I_{b} + (k + k_{p s} + k_{s} + k_{p a}) I_{k} + \frac{k_{s}}{4 π} \int_{4 π}^{} I_{k} (Ω) d Ω + \frac{k_{p s}}{4 π} \int_{4 π}^{} I_{k} (Ω) d Ω

(1734)

其中：

$k_{p a}$ 为颗粒吸收系数。
$k_{p s}$ 为颗粒散射系数。
$k_{s}$ 为散射系数。
$k_{p a}$ ， $k_{p s}$ 和 $k_{s}$ 不是波长的函数。
$Ω$ 为方向矢量。

在边界条件下

图 12. EQUATION_DISPLAY

I_{k} = ε_{w} {f (T_{w}, k) I}_{b w} + \frac{E_{w}^{d}}{π} + \frac{ρ_{w}^{d}}{π_{e f f}} \int_{(\hat{n} \cdot \hat{s})} I_{k} (s') | n \cdot s' | d Ω + ρ_{w}^{s} I_{k} (s^{i})

(1735)

其中：

图 13. EQUATION_DISPLAY

I_{k} = \int_{0}^{\infty} I_{λ} δ (k - k_{a}) d λ

(1736)

其中，光谱积分总强度由以下公式给出：

I = \int_{0}^{\infty} I_{b λ} ⅆ λ = \int_{0}^{\infty} I_{k} d k

为便于进行光谱积分，用 Eqn. (1734) 和 Eqn. (1735) 除以在给定参考状态下计算得出的 Eqn. (1736)。假定散射各向同性，由此得出：

图 14. EQUATION_DISPLAY

\frac{d I_{g}}{d s} = (k^{*} (T_{0}, ϕ, g) + {\bar{κ}}_{p}) [a (T, T_{0}, g) I_{b} (T) - I_{g}] - k_{s} (I_{g} - \frac{1}{4 π} \int_{V̵ Ω} I_{g} d Ω')

(1737)

在边界条件下

图 15. EQUATION_DISPLAY

I_{g} = ε a_{w} I_{b λ w} + \frac{ρ_{w}^{d}}{π_{e f f}} \int_{n \cdot s < 0} I_{g} (s') | n \cdot s | d Ω + ρ_{w}^{s} I_{g} (s^{s}) + τ_{w} (s^{i}) I_{g} (s^{i})

(1738)

其中：

I_{g} = I_{k} / f (T_{0}, ϕ_{0}, k)

g (T, ϕ_{0}, k) = \int_{0}^{k} f (T, ϕ_{0}, k) d k = g (T, ϕ_{0}, k^{*})

a (T, T_{0}, g) = \frac{f (T, ϕ_{0}, k)}{f (T_{0}, ϕ_{0}, k)}

a_{w} = \frac{f (T_{w}, ϕ_{0}, k)}{f (T_{0}, ϕ_{0}, k)}

高斯求积格式

k 分布法与 WSGG 法的不同之处在于其公式假设分布连续而不是步数有限，从而可以使用高阶积分方法。Wang 和 Modest 建议使用 Gauss-Chebyshev 积分法选择光谱点（在重新排序的 g 空间中）及其后续积分。介于 -1 到 1 范围内的高斯求积横坐标是特定正交多项式的零点。对于第二类 n 阶 Chebyshev 多项式，零点为：

图 16. EQUATION_DISPLAY

x_{n}^{k} = \cos (θ_{k}), k =, 1, 2, ..., n

with the corresponding Gaussian weight functions as:

w_{n}^{k} = \frac{4 \sin (θ_{k})}{n + 1} \sum_{l = 1}^{(n + 1) / 2} \frac{\sin (2 l - 1) θ_{k}}{2 l - 1}

(1739)

其中：

θ_{k} = \frac{k π}{n + 1}

对于 k 分布应用，g 空间的范围为 0 到 1，因此从上半部分中拾取求积点并对权重进行比例缩放。根据问题的不同，对此分布进行偏置可能非常有用，使得更多点位于发生大多数热传递的光谱范围内。对于辐射传输问题，这通常发生在光学中间区 (0.5 < kL < 100)，而 k 分布问题则通常发生在 g 空间 > 0.9。通过引入偏置因子，用户可以选择求积法，从而根据选择的条带数提高精度。Wang 和 Modest 引入了转换：

图 17. EQUATION_DISPLAY

{x'}_{n} = 1 - {(1 - x_{n})}^{α}

(1740)

{w'}_{n} = α w_{n} {(1 - x_{n})}^{α - 1}

Wang 和 Modest 建议对形状因子 $α$ 使用 $1.5 < α < 2.5$ 范围内的值。默认值为 1.5。

选择求积点数量和形状因子，以精确求解在特定问题中遇到的吸收系数变化。在大多数情况下，最好使用默认值 8 个点和形状因子 1.5。在极少数情况下，如果所有波段的吸收系数都很小，那么更少的点数和更大的形状因子足以求解辐射传递。