沸腾

沸腾是液体的快速汽化。通常当液体加热到超过液体的沸腾温度时发生沸腾。对于与超过液体沸腾温度的壁面接触的单组分液体，沸腾模型模拟汽化潜热效应，而不模拟蒸汽。

液体与温度 $T_{w a l l}$ 始终高于液体沸腾温度的壁面接触时，沸腾最终发生在该液体-固体交界面处。在这种情况下，在三个特征阶段发生沸腾：

泡核沸腾涉及气泡（源自表面上的离散点）在受热面上的生成和增长。表面温度只是略高于液体的饱和温度。通常，成核点数会随着表面温度的增加而增加。增加表面粗糙度可能会生成更多成核点，而非常平滑的表面可能会导致过热。
当超过临界热通量且连续蒸汽膜覆盖受热面时，会发生液膜沸腾。蒸汽层的导热率比液体低，因此蒸汽层通常隔离表面。
在介于泡核沸腾中可达到的最大温度和液膜沸腾中可达到的最小温度之间的表面温度下，会发生过渡沸腾。它是一种包含两种元素的不稳定的中间沸腾形式。

Simcenter STAR-CCM+ 中有两个不同的选项可用于沸腾建模，即：Rohsenow 沸腾模型和过渡沸腾模型。前者使用 Rohsenow 泡核沸腾模型，该模型适用于在相对较低的固体温度下沸腾。过渡沸腾模型提供泡核和过渡沸腾表达式。

Rohsenow 沸腾

Rohsenow [417] 提供的经验相关性用于计算沸腾时的表面热通量：

图 1. EQUATION_DISPLAY

q_{b w} = {μ_{l} h}_{l a t} \sqrt{\frac{g (ρ_{l} - ρ_{v})}{σ}} {(\frac{C_{p_{l}} (T_{w} - T_{s a t})}{{C_{q w} h}_{l a t} {P r}_{l}^{n_{p}}})}^{3.03}

(1829)

在此方程中， $μ_{l}$ 、 $h_{l a t}$ 、 $C_{p_{l}}$ 、 $ρ_{l}$ 和 ${P r}_{l}$ 为液相的动力粘度、潜热、比热、密度和普朗特数， $n_{p}$ 为普朗特数指数（默认为 1.73）， $g$ 为重力， $ρ_{v}$ 为蒸汽密度， $σ$ 为液体-汽体交界面处的表面张力系数， $T_{w}$ 为壁面温度， $T_{s a t}$ 为饱和温度， $C_{q w}$ 是随着液体-表面组合发生变化的经验系数。

如果应用 Rohsenow 相关性时超出其适用范围（例如，应用于薄膜沸腾区），可能导致不切实际的高热通量。流体温度可能高于近壁温度。出现此行为的原因是，Rohsenow 相关性不依赖于流体温度；进入域的热与流体温度无关。

要防止出现这种情况，将根据相关性计算的热通量乘以下列项：

图 2. EQUATION_DISPLAY

m a x [0, m i n ((\frac{T_{w} - T}{T w - T_{s a t}}), 1)]

(1830)

其中， $T$ 为加热壁面附近的流体温度。因此，如果 $T < T_{s a t}$ ，则直接使用 Rohsenow 相关性，如果 $T > T_{w}$ 沸腾热通量为零。对于介于壁面温度和饱和温度之间的流体温度，仅使用根据相关性预测的热通量分数。

过渡沸腾

过渡沸腾模型方程如下：

图 3. EQUATION_DISPLAY

q_{b o i l i n g} (Δ T) = q_{max} {S ϕ (\frac{Δ T}{Δ T_{1}})}^{K_{1}} 0 \leq Δ T \leq Δ T_{1}

(1831)

图 4. EQUATION_DISPLAY

q_{b o i l i n g} (Δ T) = q_{max} S [1 - 4 (1 - ϕ) {(\frac{Δ T - {Δ T}_{max}}{Δ T_{2} - Δ T_{1}})}^{2}] Δ T_{1} \leq Δ T \leq Δ T_{2}

(1832)

图 5. EQUATION_DISPLAY

q_{b o i l i n g} (Δ T) = q_{max} {S ϕ (\frac{Δ T}{Δ T_{2}})}^{{- K}_{2}} Δ T_{2} \leq Δ T

(1833)

上面的第一个方程模拟泡核沸腾，而其余两个方程模拟过渡 I 和过渡 II 沸腾。下图中以图形方式显示了三种流态：

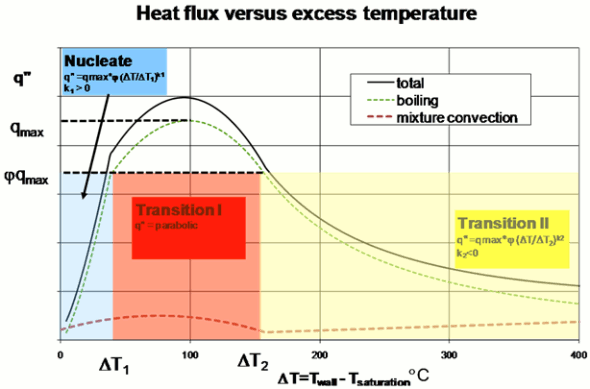
上述模型中有五个经验常数，即： $K_{1}$ 、 $K_{2}$ 、 $Δ T_{1}$ 、 $Δ T_{2}$ 和 $q_{max}$ ，所有常数均为正。 $Δ T_{m a x}$ 为 $\frac{1}{2} (Δ T_{1} + Δ T_{2})$ 。常数 $ϕ$ 设为等于 0.75。此外， $Δ T_{2}$ 必须大于 $Δ T_{1}$ 。（在上述表达式中，尽管 $K_{2}$ 是负指数，但它为正值，因为在该实现中考虑符号。）上述表达式中的比例因子 $S$ 不视为第六个常数。它可用于按比例缩放给定边界的 $q_{max}$ 。所有常数可能面向具体应用。因此，建议通过可靠测量调整常数的默认值。默认值来自 Ellion [404] 使用具有特定几何的装置进行的沸腾实验。

在过渡沸腾模型中 $Δ T_{1}$ 和 $Δ T_{2}$ 是在这三个表达式（或流态）之间切换的度量。

壁面总热通量是由沸腾、对流和热辐射引起的热通量之和。在上述方程中， $q_{max}$ 为沸腾热通量分量的最大值；它不是临界热通量（即总热通量的最大值）。曲线上与总热通量的最小值对应的点是莱登弗洛斯特点，位于过渡 II 沸腾区中。在莱登弗洛斯特点上，蒸汽完全覆盖表面，热传递主要受对流和辐射驱动，而沸腾贡献可以忽略不计。

如果流体温度 $T$ 高于饱和温度 $T_{s a t}$ ，沸腾热通量根据 Eqn. (1830) 计算。