离散坐标法数值解

离散坐标法可求解与固定方向 $s$ （以离散立体角表示）关联的辐射强度场方程。

下图演示了作为半球体一部分的离散立体角：

立体角是普通角的三维模拟，采用球面度 [ $s r$ ] 测量。1 球面度指球体表面上等于半径平方的面积所对的球体中心处的立体角。因此，整个球体的立体角为 $4 π$ 球面度。

离散坐标计算需要指定包绕任意特定点的球体离散成的立体角数量或“纵坐标”数量。增加纵坐标数可提高精度。有关方法的详细说明，请参见 Modest [398] 以及 Siegel 与 Howell [419]。根据 Eqn. (1721)，这些纵坐标方程（对于每个波长带）的形式如下：

图 1. EQUATION_DISPLAY

s_{i} \cdot \nabla I_{i Δ λ} = - β_{Δ λ} I_{i Δ λ} + k_{a Δ λ} I_{b Δ λ} + \frac{k_{s Δ λ}}{4 π} \sum_{j = 1}^{n} w_{j} I_{j Δ λ} + {\bar{k}}_{p α Δ λ} I_{p b Δ λ} + \frac{{\bar{k}}_{p s Δ λ}}{4 π} \sum_{j = 1}^{n} w_{j} I_{j Δ λ}

(1741)

在上述方程中， $Δ λ$ 表示从 $λ_{m}$ 到 $λ_{n}$ 之间的波长带。

此波长带范围内的黑体辐射为：

图 2. EQUATION_DISPLAY

I_{b Δ λ} = \int_{0}^{λ_{n}} I_{b λ} d λ - \int_{0}^{λ_{m}} I_{b λ} d λ

(1742)

边界条件

使用与其他传输方程相同的离散化和迭代求解方法，单独对每个坐标方向的传输方程进行离散化和求解。因此，需要执行全局迭代才能包含 RTE 中的各向同性内散射项以及计算壁面边界条件。角度化离散的边界条件的形式如下：

图 3. EQUATION_DISPLAY

I_{i Δ λ, w} = ε_{w Δ λ} I_{b Δ λ} + \frac{ρ_{w Δ λ}^{d}}{π_{eff}} \sum_{(n \cdot s^{'} < 0)}^{} I_{j Δ λ} {| n \cdot {s^{'}}_{j} |}_{w} + f ρ_{w Δ λ}^{s} I_{Δ λ} (s^{s}) + τ_{w Δ λ} I_{i Δ λ}

(1743)

其中：

$π_{e f f}$ 为所选纵坐标集的半矩，定义如下：
图 4. EQUATION_DISPLAY

$π_{eff} = \sum_{n \cdot s^{'} > 0}^{} w_{j} {(n \cdot {s^{'}}_{j})}_{w}$

(1744)
$f$ 为校正因子，在镜面反射的方向与任何离散纵坐标方向都不对齐时使用。

漫反射项表示进入（入射）纵坐标方向上的总和。

使用连续空间角度扫掠得到的入射能量中的标准化差值的无穷范数来衡量收敛。

辐射源项

辐射求解向流体动能方程（由 Eqn. (1727) 给出）提供了一个源项。此源项在任何网格单元处的离散形式如下：

图 5. EQUATION_DISPLAY

- \nabla \cdot q_{r} = \sum_{λ}^{} k_{a Δ λ} (\sum_{j = 1}^{n} w_{j} I_{j Δ λ} - 4 π I_{b Δ λ})

(1745)

颗粒吸收

给定网格单元内所有颗粒（拉格朗日粒子束）的辐射能量净吸收速率如下：

图 6. EQUATION_DISPLAY

- \nabla \cdot q_{p r} = \sum_{λ}^{} {\bar{k}}_{p a Δ λ} (\sum_{j = 1}^{n} w_{j} I_{j Δ λ} - 4 π I_{p b Δ λ})

(1746)

对于拉格朗日颗粒传输，收敛时，此物理量会恰好平衡网格单元中所有颗粒吸收的净辐射能量。

等效颗粒吸收和散射系数在 [398] 中给出，如下：

图 7. EQUATION_DISPLAY

{\bar{k}}_{p a Δ λ} = \sum_{i}^{} Q_{a, i} N_{i} \frac{π d_{i}^{2}}{4}

(1747)

图 8. EQUATION_DISPLAY

{\bar{k}}_{p s Δ λ} = \sum_{i}^{} Q_{s, i} N_{i} \frac{π d_{i}^{2}}{4}

(1748)

其中：

$i$ 为粒子束索引号。
$Q_{a, i}$ 为第 $i$ 个粒子束的吸收系数。
$Q_{s, i}$ 为第 $i$ 个粒子束的散射系数。
$N_{i}$ 为第 $i$ 个粒子束的每单位体积的颗粒数。
$d_{i}$ 为 $i$ 个粒子束的颗粒直径。

离散纵坐标求积

使用边界条件 (Eqn. (1743)) 求解 Eqn. (1741) 所需的纵坐标集是使用离散纵坐标求积格式获取的。DOM 求积格式 [409] 的一般原理如下：

必须将所有离散纵坐标 $Ω_{m} = (ζ_{m}, η_{m}, μ_{m})$ （其中， $(ζ_{m}, η_{m}, μ_{m})$ 为方向余弦）放置在单位球体上，即：
图 9. EQUATION_DISPLAY

$(ζ_{m}^{2} + η_{m}^{2} + μ_{m}^{2}) = 1$
(1749)
与每个纵坐标方向关联的权重必须全部为正值。这一要求确保了尽可能减小求积格式的误差。
保留的光子数必须与满足以下方程的光子数相等：
图 10. EQUATION_DISPLAY

$\sum_{m = 1}^{M} w_{m} (n \overline{Ω_{m}}) = 0$
(1750)

其中， $w_{m}$ 为与纵坐标关联的权重， $n$ 为任意单位矢量。
对于围绕单位球体中心的离散方向布局的任意旋转，求积不得变化。

尽管可轻松满足前三个条件，但是对于有限数量纵坐标的任意旋转，无法满足第四个条件。因此，所有纵坐标集必须至少满足零阶矩、一阶矩和二阶矩。为了确保辐射计算的精度，纵坐标集与权重还必须满足三个主方向上一半范围内的一阶矩。此表达式如下：

图 11. EQUATION_DISPLAY

\sum_{n \overline{Ω_{m}} > 0}^{} w_{m} (n \overline{Ω_{m}}) = π

(1751)

额外要求基于以下内容：

壁面处的辐射强度可以具有方向不连续性。
壁面处的重要辐射热通量通过 $2 π$ 的一半范围内的一阶矩计算。

层对称 (Sn) 求积

层对称（也称为 Sn）求积指离散纵坐标在单位球体的纬度方向上排列的求积格式。对应的纬度在 x 方向、y 方向和 z 方向上的距离相同，因此此求积格式被称为层对称求积。下图说明了一个典型布局（n = 6 时的对称点布局）[410]。

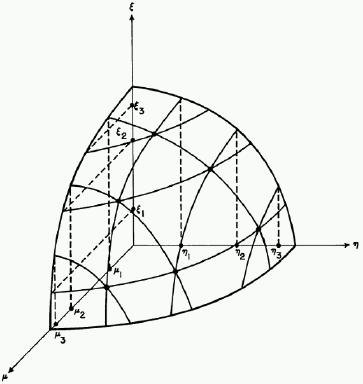
纬度方向上的布局致使主八面体的旋转不变性得到隐式满足。由于布局基于纬度，因此可在三维和轴对称二维问题的离散纵坐标方程的求解中使用 Sn 求积。目前，Simcenter STAR-CCM+ 中仅提供 Sn 求积。Sn 求积可设定为满足奇数矩或偶数矩。要查找满足特定矩的 Sn 公式，请参见下表。Sn(O) 为奇数公式，Sn(E) 为偶数公式。


	类型
阶数	Sn(O)	Sn(E)
2	0、1	0、2
4	0、1、2	0、2、4
6	0、1、2、3	0、2、4、6
8	0、1、2、3、4	0、2、4、6、8
12	0、1、2、3、4、5、6	0、2、4、6、8、10、12
16	0、1、2、3、4、5、6、7、8	0、2、4、6、8、10、12、14、16

采用奇数公式的所有 Sn 求积 ( $N > 2$ ) 都满足满足零阶矩、一阶矩和二阶矩的主要要求，而偶数公式不满足。但是，Sn 的奇数公式会导致权重为负（对于 $N \geq 10$ ），因此它们通常由于不准确而不适用。Sn 的偶数公式不会造成该问题，N = 10 时除外。因此，在 Simcenter STAR-CCM+ 中，N = 2、4、6 和 8 时，可使用奇数公式；N = 12 和 16 时，可使用偶数公式。在 Simcenter STAR-CCM+ 中，上述所有可用 Sn 求积都满足沿主方向的半矩条件。