具有固定壁面边界的旋转流体的能量平均

对于旋转机械模拟，Simcenter STAR-CCM+ 提供了使用移动（旋转）参考坐标系对旋转流体进行建模的选项。通常情况下，流体以指定的旋转速度随参考坐标系旋转，而固定罩体建模为驻留在另一参考坐标系上的固定壁面边界。由于流体（以及相关叶片）旋转，因此需要对固定壁面边界处的热传递分布进行平均。圆周平均在径向离散间隔上执行。要计算旋转流体区域内侧的平均热通量，以及对周围固定壁面边界的平均热影响，可考虑将观察器放置在固定边界上并查看旋转的内部介质的内部。

根据壁面边界热指定，将以不同的方式计算能量平均值。

热通量

壁面处热通量的常规方程

q_{w}

为：

图 1. EQUATION_DISPLAY

\bar{h_{c} T_{c}} - \bar{h_{c}} T_{w} + \bar{q_{a b s p, w}^{r}} - σ ϵ_{w}^{total} T_{w}^{4} = - q_{w}

(1821)

其中：

$\bar{h_{c}}$ 为网格单元中心和边界面之间的流体在内侧的面积平均热传递系数。
$\bar{T_{c}}$ 为面积平均网格单元温度。
$T_{w}$ 为壁面温度。
$\bar{q_{absp, w}^{r}}$ 为边界处吸收的辐射热通量。
$ϵ_{w}^{total}$ 为总壁面发射率。

对于边界热通量系数， $q_{w}$ 方程为：

图 2. EQUATION_DISPLAY

\bar{a} + \bar{b T_{c}} + \bar{c} T_{w} + d T_{w}^{4} = - q_{w}

(1822)

为便于边界处的能量线性化，Eqn. (1822) 写作：

图 3. EQUATION_DISPLAY

\bar{a} + \bar{b_{eff}} T_{c} + \bar{c} T_{w} + d T_{w}^{4} = - q_{w}

(1823)

其中：

$a = \bar{q_{absp, w}^{r}}$
$b = \bar{h_{c}}$
$c = - \bar{h_{c}}$
$d = - σ ϵ_{w}^{total}$
$\bar{b_{eff}} = \frac{\bar{b T_{c}}}{T_{c}}$

如果在边界处激活外部辐射，对于外部表面，上述方程 Eqn. (1821)、Eqn. (1822) 和 Eqn. (1823) 的方程右侧还包含辐射排放项和吸收项 $(σ ϵ_{w, e x t}^{total} T_{w}^{4} - \bar{q_{absp, w, ext}^{r}})$ 。

绝热

这是一个热通量条件特例，其中

q_{w} = 0

。平均适用于热通量条件。

热源

这类似于热通量条件，除非热源项先转换为每个边界面应用的热通量。

温度

这里使用 Eqn. (1823)，除非边界温度 $T_{w}$ 已知且热通量 $q_{w}$ 已计算。

对流

不存在热阻时

平均值与 Eqn. (1821) 相同，但右侧具有对流热通量，而不是指定的热通量：

图 4. EQUATION_DISPLAY

\bar{h_{c} T_{c}} - \bar{h_{c}} T_{w} + \bar{q_{absp, w}^{r}} - σ ϵ_{w}^{total} T_{w}^{4} = h_{\infty} (T_{w} - T_{\infty})

(1824)

其中， $T_{\infty}$ 和 $h_{\infty}$ 是环境的温度和热传递系数。

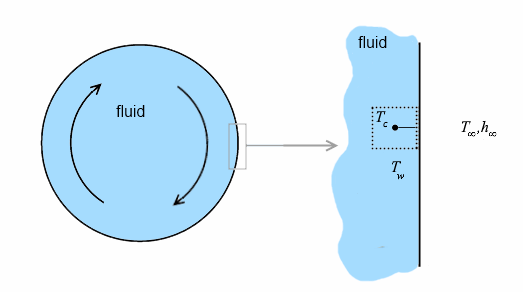
使用边界热通量系数时，此方程可以写为：

\bar{a} + \bar{b_{eff}} T_{c} + \bar{c} T_{w} + d T_{w}^{4} = h_{\infty} (T_{w} - T_{\infty})

当激活外部辐射时，对于外部表面，上述方程和 Eqn. (1824) 的右侧还包含辐射排放项和吸收项。

存在热阻时

边界条件会考虑环境和热阻的影响。

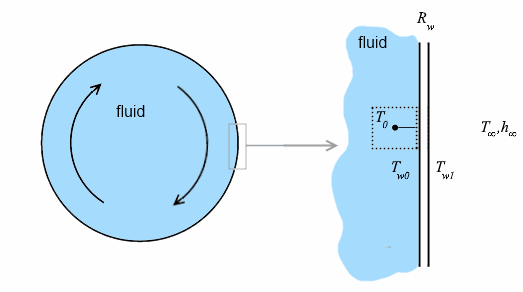
要求解的方程包括：

对于内部边：
图 5. EQUATION_DISPLAY

$\bar{h_{c} T_{c}} - \bar{h_{c}} T_{w 0} + \bar{q_{a b s p, 0}^{r}} - σ ϵ_{0}^{total} T_{w 0}^{4} = \frac{T_{w 0} - T_{w 1}}{R_{w}}$

(1825)
对于外部侧：
图 6. EQUATION_DISPLAY

$h_{\infty} (T_{\infty} - T_{w 1}) + \bar{q_{a b s p, 1}^{r}} - σ ϵ_{1}^{total} T_{w 1}^{4} = \frac{T_{w 1} - T_{w 0}}{R_{w}}$

(1826)

其中：

$T_{w 0}$ 是内表面上的壁面温度。
$T_{w 1}$ 是外表面上的壁面温度。
$R_{w}$ 是壁面的热阻。

对于边界热通量系数，这些方程变为：

对于内部边：
图 7. EQUATION_DISPLAY

$\bar{a_{0}} + \bar{b_{0 eff}} T_{c 0} + \bar{c_{0}} T_{w 0} + d_{0} T_{w 0}^{4} = \frac{Δ T_{w}}{R_{w}}$

(1827)
其中， $Δ T_{w} = T_{w 0} - T_{w 1}$ 。
对于外部侧：
图 8. EQUATION_DISPLAY

$a_{1} + h_{\infty} T_{\infty} - h_{\infty} T_{w 1} + d_{1} T_{w 1}^{4} = \frac{- Δ T_{w}}{R_{w}}$

(1828)