Conjugate Heat Transfer

A conjugate heat transfer (CHT) problem is solved across a contact interface, where different materials, such as fluid and solid or a porous medium and solid, exist on the two sides of the defined interface.

Conjugate Heat Transfer Between Fluid and Solid

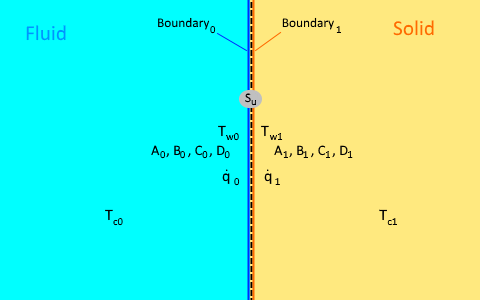
Based on the conservation of energy, total heat flux is conserved across the interface. At a contact interface, two boundaries are defined, Boundary₀ in the fluid region and Boundary₁ in the solid region.

Energy conservation assures that:

图 1. EQUATION_DISPLAY

{\dot{q}}_{0} + {\dot{q}}_{1} = - S_{u}

(1681)

where:

${\dot{q}}_{0}$ is the heat flux from the fluid through Boundary₀.
${\dot{q}}_{1}$ is the heat flux leaving through Boundary₁ into the solid.
$S_{u}$ is an optional user-specified heat source within the interface.

The heat flux on each side of the interface can be expressed in terms of linearized heat flux coefficients as given by Eqn. (202).

Therefore, on Boundary₀:

图 2. EQUATION_DISPLAY

{\dot{q}}_{0} = A_{0} + B_{0} T_{c 0} + C_{0} T_{w 0} + D_{0} T_{w 0}^{4}

(1682)

and similarly on Boundary₁:

图 3. EQUATION_DISPLAY

{\dot{q}}_{1} = A_{1} + B_{1} T_{c 1} + C_{1} T_{w 1} + D_{1} T_{w 1}^{4}

(1683)

where:

$A$ , $B$ , $C$ , and $D$ are the linearized heat flux coefficients.
$T_{c 0}$ , $T_{c 1}$ are the cell temperatures next to Boundary₀ and Boundary₁ respectively.
$T_{w 0}$ , $T_{w 1}$ are the interface temperatures on the fluid side (Boundary₀) and on the solid side (Boundary₁) respectively.

Since the temperature can be different on the two sides of the interface, the heat flux across the interface is expressed with respect to the interface temperature difference and a user-specified value for interface thermal resistance $R$ :

图 4. EQUATION_DISPLAY

{\dot{q}}_{0} = - \frac{S_{u}}{2} + \frac{T_{w 1} - T_{w 0}}{R}

(1684)

Eventually, Eqn. (1681) to Eqn. (1684) are solved for the four unknowns ( ${\dot{q}}_{0}$ , ${\dot{q}}_{1}$ , $T_{w 0}$ , and $T_{w 1}$ ), either analytically or numerically. The solution is done analytically in the absence of a radiation term, when $D_{0}$ and $D_{1}$ are zero, so a linear system of equations is obtained. If $D_{0}$ and $D_{1}$ are not zero, the solution is obtained numerically.

Conjugate Heat Transfer Between Solid and Solid: The conjugate heat transfer problem at solid/solid contact interfaces is solved in the same way as at fluid/solid interfaces.

Conjugate Heat Transfer Between Fluid with Porous Media Model and Solid

At this contact interface, two boundaries are defined, Boundary₀ in the porous region and Boundary₁ in the solid region.

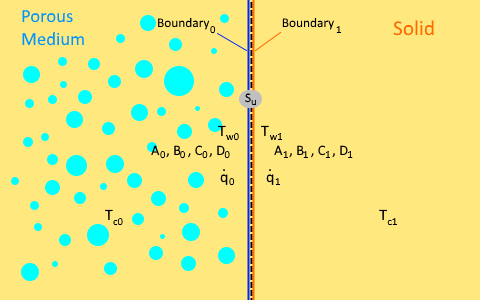
When a solid region is in contact with a porous medium that is modeled using the physical velocity approach, Simcenter STAR-CCM+ uses the following assumptions:

At a contact boundary in the phasic-porous region, an involved phase (fluid or solid) can participate in the CHT or can be treated as adiabatic.
All the involved phases on each interface boundary, which are participating in the CHT as well, are at thermal equilibrium. Therefore, there is only one averaged temperature on each interface side ( $\bar{T_{w 0}}$ and $\bar{T_{w 1}}$ ).
Heat flux coefficients are averaged among all involved and participated phases. For instance, for a porous medium $\bar{ϕ} = Σ_{i} α_{i} η_{i} ϕ_{i}$ ,where $ϕ$ is any of the linearized heat flux coefficients ( $A$ , $B$ , $C$ , and $D$ ), $α_{i}$ and $η_{i}$ are the volume fraction and available volume fraction of phase $i$ , respectively.
Heat flux is zero for the phases that are excluded from the CHT and are treated as adiabatic, so they are mathematically excluded from conservation of energy (Eqn. (1681). For these phases, the temperature at the contact boundary is updated based on the adiabatic condition assumption. As a result, a unique temperature is obtained for each non-participating phase, different from the phase-averaged temperatures ( $\bar{T_{w 0}}$ and $\bar{T_{w 1}}$ ).