多层液膜铸造

液膜铸造是指从槽模中挤出薄膜，然后在薄膜熔融的同时，用冷金属辊进行拉伸的工艺。薄膜可以包含一层或多层。在铸造工艺中，拉伸的主要目的是将薄膜的厚度减小到所需的水平。薄膜的厚度要远小于其长度和宽度，因此，要分析此问题，必须使用薄膜模型。

下图显示了多层液膜铸造工艺的示意图：

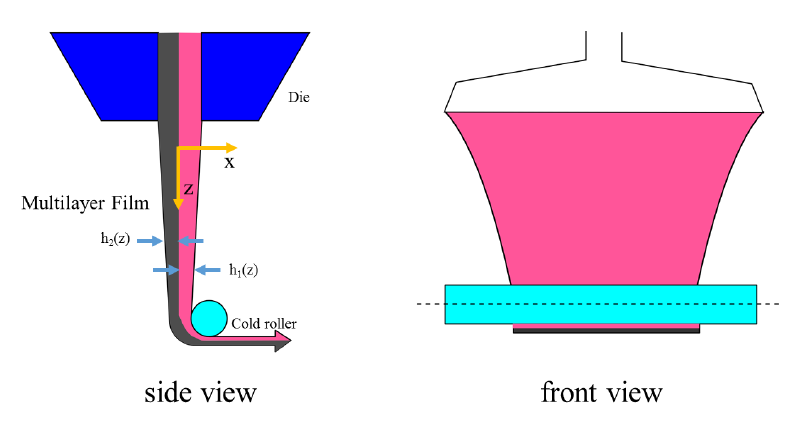
薄膜层厚度 $i$ 由 $z$ 方向的 $h_i\text{, i=1,}\dots N$ 表示，其中 $N$ 表示层数。相比薄膜的长度和宽度，薄膜的厚度可忽略不计，即 $h_i\ll l\sim w$ 。因此，要获得相应的控制方程，描述处于非稳态下且含有多种不可压缩的粘弹性流体的薄膜的动力学，可合理假定在厚度方向 $z$ 的速度分量变化 $x$ 和 $y$ 可忽略不计，而且 $v_z$ 仅是 $z$ 的函数 [233]：

使用流体的不可压缩性条件，它可表示为：

其中， ${\nabla }_s=(\mathbf{I}-{\mathbf{e}}_z{\mathbf{e}}_z)\cdot \nabla$ 。 ${\nabla }_s$ 是表面梯度运算符， ${\mathbf{e}}_z$ 是 $z$ 方向的单位法向矢量，而 $\mathbf{I}$ 是单位张量。

对有厚度的薄膜施加力平衡：

在 $x$ 和 $y$ 方向，根据薄膜动量平衡，假设 $z$ 方向无应力且等应变，并忽略边界处（即毛细管数较多）的交界面张力，此时薄膜的动量方程可以写为：

其中：

• ${\rho }_i$ 为层 $i$ 的流体密度。
• $p_i$ 为压力。
• ${\tau }_i$ 为第 $i$ 层的流体动力应力张量。

总流体动力应力张量 ${\mathbf{T}}_i$ 可以定义为 ${\mathbf{T}}_i=2{\mu }_i\mathbf{D}+{\mathbf{T}}_i^p$ ，其中：

• ${\mu }_i$ 为与第 $i$ 层关联的溶剂粘度。
• $\mathbf{D}$ 为应变率张量。
• ${\mathbf{T}}_i^p$ 为对与第 $i$ 层关联的应力张量的粘弹性贡献。

由于必须满足薄膜的局部质量守恒，因此：

薄膜的能量方程可以写为：

其中：

• $C_{p_i}$ 为第 $i$ 层流体的比热容。
• $T$ 为温度。
• $k_i$ 为第 $i$ 层流体的导热率。
• $q_{\text{conv}}$ 和 $q_{\text{rad}}$ 是通过薄膜的顶部和底部边界的相应对流和辐射热通量。
  $$\begin{array}{c}{q}_{\text{conv}}=h_c(T-T_{\infty })\\ q_{\text{rad}}=\sigma ϵ(T^4-T_{\infty }^4)\end{array}$$

  其中：

  • $T_{\infty }$ 为环境温度。
  • $h_c$ 为薄膜（顶面和底面）的整体对流热传递系数。
  • $\sigma$ 为玻尔兹曼常数。
  • $ϵ$ 为发射率因子。

聚合物和溶剂的材料属性是根据适当的时间-温度叠加定律（例如 Arrhenius、WLF 或 Nahme 定律）确定的温度函数。