体积分区

当模拟双向耦合拉格朗日多相流或离散多相 (DMP) 流时，离散相的体积将减去连续流体所占的实际体积和计算通量的实际面积。对于液膜模拟，与液膜相邻的流体的可用体积小于网格单元体积。同样，在使用物理速度公式的多孔介质建模中，一部分网格单元体积被固相占据，因此减少流体的可用体积。对于二维模型，假定网格具有单位深度（以 SI 单位表示）。

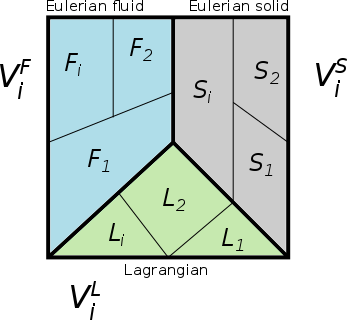
在下图中，网格单元体积 $V$ 的体积分区可以由流体体积 $V^F$、多孔固体体积 $V^S$ 和离散相体积（此处为拉格朗日颗粒）体积 $V^L$ 之和组成，每个体积都可以由下标 $i$ 所指示的各个相组成：

总网格单元体积由以下公式给出：

流体 $\eta$ 的可用体积分数则定义为所有液相所占体积与总网格单元体积之比：

流体 ${\alpha }_i$ 的一个相的体积分数定义为该相所占体积与总流体域体积之比：

其中，${\displaystyle \sum _i^{}{\alpha }_i=1}$

对于体积分区，通过使用无量纲流体体积分数 ${\alpha }_i$ 和可用体积分数 $\eta$ 来对控制流体流方程 Eqn. (664) 至 Eqn. (666) 进行比例缩放：

连续性方程

$$\frac{\partial }{\partial t}\underset{V}{\int }{\alpha }_i\eta \rho dV+{\oint }_A{\alpha }_i\eta \rho v\cdot da=\underset{V}{\int }{S}_{u}dV+\underset{V}{\int }{S}_{\mathrm{int}}dV$$

(874)

动量方程

$$\begin{array}{c}\frac{\partial }{\partial t}\underset{V}{\int }{\alpha }_i\eta \rho \mathbf{\text{v}}dV+\underset{A}{\overset{}{\oint }}{\alpha }_i\eta \rho v\otimes v\cdot d\mathbf{\text{a }}=\end{array}-{\oint }_A{\alpha }_i\eta pI\cdot da+{\oint }_A{\alpha }_i\eta T\cdot da+\underset{V}{\int }{\alpha }_i\eta f_{b}dV+\underset{V}{\int }{s}_{u}dV+\underset{V}{\int }{s}_{\mathrm{int}}dV$$

(875)

能量方程

$$\frac{\partial }{\partial t}\underset{V}{\int }{\alpha }_i\eta \rho EdV+{\oint }_A^{}{\alpha }_i\eta \mathrm{\rho H}v\cdot d\mathbf{\text{a}}=-{\oint }_A^{}{\alpha }_i\eta \mathbf{\text{q}}\cdot d\mathbf{\text{a}}+{\oint }_A^{}{\alpha }_i\eta \mathbf{\text{T}}\mathbf{\cdot }\mathbf{\text{v}}d\mathbf{\text{a}}+\underset{V}{\int }{\alpha }_i\eta {\mathbf{\text{f}}}_b\mathbf{\cdot }\mathbf{\text{v}}dV+\underset{V}{\int }{S}_{u}dV+\underset{V}{\int }{S}_{\mathrm{int}}dV$$

(876)

其中 $S_u,s_u$ 是用户源项，$S_{\mathrm{int}}$ 是由建模交互引起的内部源项。

如果要对组分或被动标量求解，则相应的传输方程 (Eqn. (1871) 和 Eqn. (1899)) 也会受到体积分区的影响：

组分传输

$$\frac{\partial }{\partial t}\underset{V}{\int }{\alpha }_i\eta \rho Y_i\mathrm{dV}+\underset{A}{\oint }{\alpha }_i\eta \rho Y_i\mathbf{\text{v}}\cdot da=\underset{A}{\oint }{\alpha }_i\eta [J_i+\frac{{\mu }_t}{{\sigma }_t}\nabla Y_i]\cdot da+\underset{V}{\int }{S}_{Y_i}dV$$

(877)

被动标量传输

$$\frac{\partial }{\partial t}\underset{V}{\int }{\alpha }_i\mathrm{\eta \rho }{\varphi }_{i}dV+\underset{A}{\oint }{\alpha }_i\mathrm{\eta \rho }{\varphi }_i\mathbf{\text{v}}\cdot da=\underset{A}{\oint }{\alpha }_i\eta j_i\cdot da+\underset{V}{\int }{S}_{{\varphi }_i}dV$$

(878)