状态方程

恒密度

ρ = ρ_{0}

(669)

其中， $ρ_{0}$ 为常数。

多项式密度

对于气体、液体和固体，密度可按多项式的形式指定为温度 $T$ 的函数。温度范围可以细分为多个间隔，每个都具有自己的多项式函数：

图 1. EQUATION_DISPLAY

ρ = \sum_{i = 0}^{n} {a_{i} \cdot T}^{i - 1}

(670)

其中， $a$ 为多项式系数。

理想气体

理想气体定律将密度表示为温度和压力的函数：

图 2. EQUATION_DISPLAY

ρ = \frac{p}{R T}

(671)

其中：

$p$ 为压力
$R$ 为单位气体常数

和

图 3. EQUATION_DISPLAY

R = R_{u} / M

(672)

其中：

$R_{u}$ 为通用气体常数 [8314.4621 J/kmol K]
$M$ 为分子量

实际气体

在高压和低温条件下，实际气体的 p-v-T 行为与理想气体方程预测的行为有所偏差。这一行为变化是由于随着气体密度增加，气体分子占据了总体积的大部分。此外，分子间引力变得越来越重要。

Van der Waals

van der Waals 方程由以下公式给出：

图 4. EQUATION_DISPLAY

(p + a / v^{2}) (v - b) = R T

(673)

Van der Waals 将理想气体关系中的单位体积 $p v = R T$ 替换为 $(v - b)$ ，以考虑气体颗粒占据的体积，同时将压力替换为项 $(p + a / v^{2})$ 。常数 $b$ 为颗粒的本身体积，常数 $a$ 用于衡量引力。

常数 $a$ 和 $b$ 基于实验观察结果计算，在 p-v 空间中，在临界状态下（ $p = p_{c}$ 且 $v = v_{c}$ ），临界等温 $T = T_{c} = constant$ ，斜率为零并且具有拐点。因此，存在以下等式：

图 5. EQUATION_DISPLAY

\frac{d p}{d v} | T_{c} = 0

(674)

和

图 6. EQUATION_DISPLAY

\frac{d^{2} p}{{d v}^{2}} | T_{c} = 0

(675)

从而获得 $a$ 和 $b$ 的以下表达式：

图 7. EQUATION_DISPLAY

a = \frac{27}{64} \frac{R^{2} T_{c}^{2}}{p_{c}}, b = \frac{1}{8} \frac{R T_{c}}{p_{c}}

(676)

通过上述方程，可根据临界压力 $p_{c}$ 和临界温度 $T_{c}$ 的实验测量值确定 $a$ 和 $b$ 。

Peng-Robinson

Peng-Robinson 方程由以下公式给出：

图 8. EQUATION_DISPLAY

p = \frac{R T}{(v - b)} - \frac{a α (T_{r})}{(v^{2} + 2 b v - b^{2})}

(677)

其中， $v$ 为单位体积。

函数

α (T_{r})

由以下公式给出：

图 9. EQUATION_DISPLAY

α (T_{r}) = {[1 + (0.37464 + 1.54226 ω - 0.2699 ω^{2}) (1 - {T_{r}}^{0.5})]}^{2}

(678)

其中， $T_{r} = T / T_{c}$ 为折算温度， $ω$ 为气体的离心因子。

常数为：

图 10. EQUATION_DISPLAY

a = \frac{0.4572 R^{2} T_{c}^{2}}{p_{c}}, b = \frac{0.0778 R T_{c}}{p_{c}}

(679)

Redlich-Kwong: Redlich-Kwong 方程由以下公式给出：

图 11. EQUATION_DISPLAY

$p = \frac{R T}{(v - b)} - \frac{a}{[T^{0.5} v (v + b)]}$

(680)
且
图 12. EQUATION_DISPLAY

$a = \frac{0.4275 R^{2} T_{c}^{2}}{p_{c}}, b = \frac{0.0867 R T_{c}}{p_{c}}$

(681)

Soave-Redlich-Kwong: Soave 修正了 Redlich-Kwong 方程，将 Eqn. (681) 的分母中的 $T^{0.5}$ 幂替换为不同的温度相关表达式 [210]。此修正改进了液体密度和汽-液平衡的预测，如下所示：
图 13. EQUATION_DISPLAY

$p = \frac{R T}{v - b} - \frac{a α (T_{r})}{v (v + b)}$

(682)
函数 $α (T_{r})$ 为：
图 14. EQUATION_DISPLAY

$α (T_{r}) = {[1 + (0.48 + 1.574 ω - 0.176 ω^{2}) (1 - T_{r}^{0.5})]}^{2}$

(683)
且
图 15. EQUATION_DISPLAY

$a = \frac{0.42748 R^{2} T_{c}^{2}}{p_{c}}, b = \frac{0.08664 R T_{c}}{p_{c}}$

(684)

已修正的 Soave-Redlich-Kwong 模型: Graboski 和 Daubert 修正了 Soave-Redlich-Kwong 模型，以改进其涉及非极性分子 [173] 和 [174] 的相平衡计算的行为。所有方程仍与 Soave-Redlich-Kwong 模型相同，唯一区别为函数 $α (T_{r})$ 更改为：
图 16. EQUATION_DISPLAY

$α (T_{r}) = {[1 + (0.48503 + 1.55171 ω - 0.15613 ω^{2}) (1 - T_{r}^{0.5})]}^{2}$

(685)

平衡空气

对于高温下的空气，分子离解、内能激励和电离效应变得明显。

在这些效应的时间尺度比流的时间尺度短得多的情况中，可以按平衡方式处理这些效应。在这种情况下，流体属性（如密度、比热和传输属性）将变为两个热力学变量的表达式。这些表达式通常采用曲线拟合形式，考虑了在高温下出现的化学反应和能量模式。尤其是，使用了 Gupta 等人的 [176] 提出的曲线拟合。这些曲线拟合将可压缩性因子、比热、焓、粘度和导热率指定为温度与压力的函数。曲线拟合适用于低于 30,000 K 的温度和介于 10^-4 和 10² 个大气压之间的压力。

平衡空气状态方程将可压缩性因子作为场函数提供。在此模型上下文中，可压缩性因子表示空气的未离解分子量与平均分子量之比 [176]：

图 17. EQUATION_DISPLAY

Z (T, P) = \frac{M_{o}}{\bar{M}}

(686)

其中， $M_{o}$ 表示未离解空气的分子量， $\bar{M}$ 表示给定温度和压力下的空气平均分子量。由于平均分子量为成分的函数，因此可压缩性因子可用于衡量空气中的离解程度，值越高，表示离解和电离程度越大。

热非平衡

对于气体，内能包含了平移、旋转、振动和电子模式。在平衡状态下，可通过单个特征温度充分描述这些能量模式。在热非平衡状态下，平移和旋转能量模式由一个温度描述，而振动和电子能量模式由额外的振动-电子温度描述。振动-电子温度通过求解额外的能量方程确定，该方程描述了振动-电子能量的守恒。Gnoffo 等人的 [172] 提出了此方程，Lockwood [192] 将其简化为非电离流体：

图 18. EQUATION_DISPLAY

\begin{matrix} \frac{\partial ρ e_{v e}}{\partial t} + \nabla \cdot (ρ e_{v e} U) = \nabla \cdot (k_{v e} \nabla T) + \nabla \cdot (ρ \sum_{s}^{} h_{v e, s} D_{s} {\nabla y}_{s}) \\ + \sum_{s = mol}^{} ρ_{s} \frac{(e_{v, s}^{*} - e_{v, s})}{< τ_{s} >} + \sum_{s = mol}^{} {\dot{ω}}_{s} e_{v e, s} \end{matrix}

(687)

振动-电子能量和平移-旋转能量的交换通过松弛项进行建模。在 Gnoffo 等人的 [172] 提出了此松弛并提供了简化，以便减少计算中包含的组分相关参数：

图 19. EQUATION_DISPLAY

e_{v, s}^{*} - e_{v, s} \approx C_{v, v}^{s} (T - T_{v})

(688)

图 20. EQUATION_DISPLAY

\sum_{s = mol}^{} \frac{ρ_{s} C_{v, v}^{s}}{〈 τ_{s} 〉} \approx \frac{ρ C_{v, v}^{s}}{{\bar{τ}}_{v}}

(689)

要描述振动-电子焓和温度之间的关系，必须指定振动比热。此振动比热通过同时设置总比热和平移 - 旋转比热指定。对于此模型，平移 - 旋转能量模式假设为全激励 $(F - E)$ ，因此平移 - 旋转比热恒定 $(C_{p, t r})$ 。指定这两个值后，振动比热和焓由 [172] 给出：

图 21. EQUATION_DISPLAY

C_{p, v e} (T_{v e}) = C_{p, total} (T_{v e}) - C_{p, t r}^{F - E}

(690)

图 22. EQUATION_DISPLAY

h_{v e} (T_{v e}) = h_{total} (T_{v e}) - C_{p, t r}^{F - E} (T_{v e} - T_{ref}) - h_{o}

(691)

IAPWS-IF97

使用 IAPWS-IF97（水与蒸汽特性国际协会，行业规定 1997）的模型，可以运行液态水或气态蒸汽的模拟。

此类模型包含密度和其他热力学属性的计算。IAPWS-IF97 为比吉布斯自由能 $g (p, T)$ 提供了基本多项式方程。单位体积、内能、熵、焓、热容和声速均可通过该基本方程，使用无量纲吉布斯自由能及其导数 [182] 的适当组合推导得出。

根据吉布斯自由能，Simcenter STAR-CCM+ 中的 IAPWS-IF97 模型仅适用于特定范围的温度和压力。这些范围在区域示意图中表示 [182]，这些区域实质上代表了水与蒸汽的各个相。

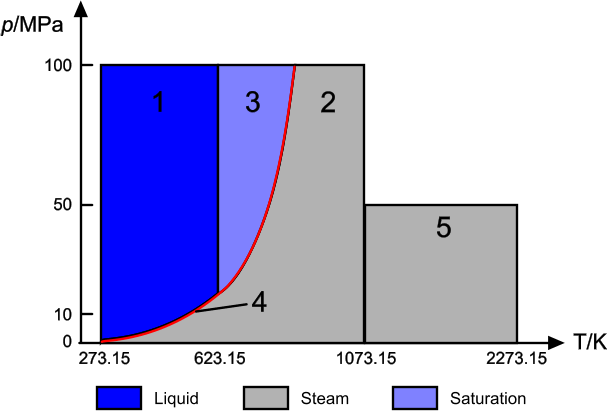
下表列出了区域示意图的各个组成部分以及它们如何与 Simcenter STAR-CCM+ 中的 IAPWS-IF97 模型搭配使用。


组成部分	有效范围		STAR-CCM+ 模型
区域 1（液体）	273.15 K ≤ T ≤ 623.15 K	p ≤ 100 MPa	IAPWS-IF97（水）
区域 2（蒸汽）	273.15 K ≤ T ≤ 1073.15 K	p ≤ 100 MPa	IAPWS-IF97（蒸汽）
区域 3（饱和）	Simcenter STAR-CCM+ 不支持此相区域。
边界 4	此边界的一侧为液体与饱和，另一侧为蒸汽。
区域 5（蒸汽）	1073.15 K < T ≤ 2273.15 K	p ≤ 50 MPa	IAPWS-IF97（蒸汽）

过热液体的焓 $H_{s h}^{L}$ 和过冷蒸汽的焓 $H_{s c}^{V}$ 分别计算如下：

图 23. EQUATION_DISPLAY

\begin{matrix} H_{s h}^{L} (T, P) = H_{r 1} (T_{s a t}, P) + C_{p, r 1} (T_{s a t}, P) (T - T_{s a t}) & (T > T_{s a t}) \end{matrix}

(692)

图 24. EQUATION_DISPLAY

\begin{matrix} H_{s c}^{V} (T, P) = H_{r 2} (T_{s a t}, P) + C_{p, r 2} (T_{s a t}, P) (T - T_{s a t}) & (T < T_{s a t}) \end{matrix}

(693)

其中：

$T_{s a t} (P)$ 为饱和温度
下标 $r 1$ 和 $r 2$ 分别指区域 1 和区域 2。

多组分气体

对于使用 Peng Robinson、Soave-Redlich-Kwong 或已修正的 Soave-Redlich-Kwong 方程的多组分气体， $a α (T_{r})$ 和 $b$ 基于对组分 $i$ 的几何和算术求和：

图 25. EQUATION_DISPLAY

{(a α (T_{r}))}_{mix} = {(\sum_{i = 1}^{} y_{i} \sqrt{a_{i} α_{i} (T_{r})})}^{2}, b_{mix} = \sum_{i = 1}^{} y_{i} b_{i}

(694)

其中， $y_{i}$ 为摩尔分数。