轴对称流

对于在几何与流条件下按中心轴对称的流体流，Simcenter STAR-CCM+ 可以在 2D 求解域中对该流进行建模。

质量和能量的守恒方程分别由 Eqn. (664) 和 Eqn. (666) 给出。动量的守恒方程根据是否涉及旋流来定义：

无旋流动量方程

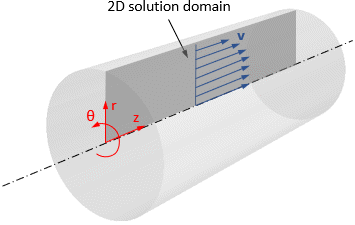
对于无旋流动量方程，Simcenter STAR-CCM+ 假设圆周速度和圆周梯度为零。

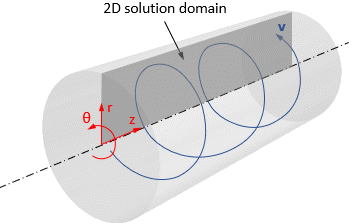
下图显示无旋流轴对称流的示例：

圆柱坐标中动量守恒方程的定义如下：

$$\begin{array}{c}\frac{\partial }{\partial t}\underset{A}{\int }\rho vrdA+\underset{\partial A}{\overset{}{\oint }}\rho v\otimes v\cdot rds\text{ =}\\ -{\oint }_{\partial A}pI\cdot rds+{\oint }_{\partial A}T\cdot rds+\underset{A}{\int }\frac{1}{r}\left[\begin{array}{c}0\\ \begin{array}{c}p-{\tau }_{\theta \theta }\\ 0\end{array}\end{array}\right]rdA+\underset{A}{\int }{f}_{b}dA+\underset{A}{\int }{s}_{u}dA\end{array}$$

(667)

且：

• $A$ 为面积。
• $\partial A$ 为 $A$ 的轮廓。
• $I$ 为单位矩阵。
• $v={\left(v_z{v}_r{v}_{\theta }\right)}^T$
• $v_{\theta }=0$ 和 $\frac{\partial }{\partial \theta }\left(\right)=0$

$T$ 为应力张量，定义为：

$T=\mu \left[\begin{array}{ccc}2\frac{\partial v_z}{\partial z}-\frac{2}{3}\nabla \cdot v& \frac{\partial v_z}{\partial r}+\frac{\partial v_r}{\partial z}& 0\\ \frac{\partial v_z}{\partial r}+\frac{\partial v_r}{\partial z}& 2\frac{\partial v_r}{\partial r}-\frac{2}{3}\nabla \cdot v& 0\\ 0& 0& 2\frac{v_r}{r}-\frac{2}{3}\nabla \cdot v\end{array}\right]$

有旋流动量方程

轴对称旋流模型将打旋或旋转流的预测加入 2D 轴对称流模拟中。如果轴对称流包括来自入口（如风扇交界面或旋转壁面）的旋流，则可以使用该模型。

下图显示具有旋流的轴对称流的示例：

假设流显示圆周速度但没有圆周梯度，则该模型求解圆柱坐标中的动量守恒公式如下：

$$\begin{array}{c}\frac{\partial }{\partial t}\underset{A}{\int }\rho vrdA+\underset{\partial A}{\overset{}{\oint }}\rho v\otimes v\cdot rds\text{ =}\\ -{\oint }_{\partial A}pI\cdot rds+{\oint }_{\partial A}T\cdot rds+\underset{A}{\int }\frac{1}{r}\left[\begin{array}{c}0\\ \begin{array}{c}p+\rho v_{\theta }^2-{\tau }_{\theta \theta }\\ -\rho v_r{v}_{\theta }+{\tau }_{\theta r}\end{array}\end{array}\right]rdA+\underset{A}{\int }{f}_{b}dA+\underset{A}{\int }{s}_{u}dA\end{array}$$

(668)

且：

• $v_{\theta }\ne 0$ 和 $\frac{\partial }{\partial \theta }\left(\right)=0$

应力张量 $T$ 定义为：

$T=\mu \left[\begin{array}{ccc}2\frac{\partial v_z}{\partial z}-\frac{2}{3}\nabla \cdot v& \frac{\partial v_z}{\partial r}+\frac{\partial v_r}{\partial z}& \frac{\partial v_{\theta }}{\partial z}\\ \frac{\partial v_z}{\partial r}+\frac{\partial v_r}{\partial z}& 2\frac{\partial v_r}{\partial r}-\frac{2}{3}\nabla \cdot v& \frac{\partial v_{\theta }}{\partial r}-\frac{v_{\theta }}{r}\\ \frac{\partial v_{\theta }}{\partial z}& \frac{\partial v_{\theta }}{\partial r}-\frac{v_{\theta }}{r}& 2\frac{v_r}{r}-\frac{2}{3}\nabla \cdot v\end{array}\right]$