S2S（表面至表面）辐射

S2S 模型基于外壳理论 [397]、[400]，并使用视角因子在块之间执行辐射能量交换。

该计算方法使用以下主要元素：

用于封闭计算域的边界和内部边界在空间上细分为连续的非重叠块。
从每个块的中心处，指定数量的光线在封闭半球体上发射，其中立体角通过角度求积进行离散。将通过计算域跟踪每条光线，直到其拦截相对块，从而定义可交换辐射能量的块对。
然后，根据辐射传输方程和边界条件计算传输到或传输自每个块的辐射能量。

表面块和视角（相互作用）因子

模型中的表面可以具有漫射或镜面反射表面属性。虽然表面发射率假定为漫射，但是反射率可以是漫射或镜面反射，并且所有透射率都为镜面反射。视角因子的计算中将考虑镜面反射属性。因此，视角因子不只是几何属性，还包括镜面反射表面属性的影响。

表面之间交换的辐射量取决于来自表面的（漫射）发射，以及表面之间的相对位置和方向。辐射量还取决于是否存在可能改变表面之间传输的任何镜面透射或反射表面。后两种影响（即，几何和镜面反射属性）可由视角（或相互作用）因子解释；根据定义，这些因子表示“从一个表面离开并直接到达另一个表面的均匀漫辐射的分数”[397]。

以下 Eqn. (1688) 到 Eqn. (1693) 用于定义灰体和漫射表面的视角因子关系。

下图显示了两个单元表面之间的辐射交换：

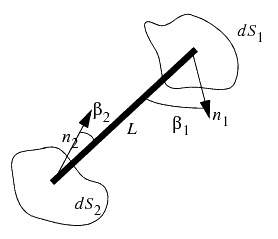
由 $d S_{1}$ 发射并由 $d S_{2}$ 接收的总辐射量功率为：

图 1. EQUATION_DISPLAY

P_{1 - 2} = {i′}_{1} d S_{1} \cos (β_{1}) (\frac{d S_{2} \cos (β_{2})}{L^{2}})

(1688)

其中：

$P_{1 - 2}$ 是离开表面 1 并在表面 2 上入射的总功率 [W]
${i′}_{1}$ 是离开表面 1 的总强度，强度被定义为“通过每单位立体角面积、传递方向每单位投影面积法向和每单位时间的辐射能量”[397] [ $\frac{W}{m^{2} s r}$ ]
$β$ 为表面法向和连接两个表面的线之间的角 [rad]
$L$ 为距离

通过采用 $d S_{2}$ 所接收的功率占 $d S_{1}$ $(P_{1} = {π i'}_{1} d S_{1})$ 发射的总辐射功率的分数，这两个表面的视角因子给定为：

图 2. EQUATION_DISPLAY

{d F}_{1 - 2} = \frac{P_{1 - 2}}{{π i'}_{1} d S_{1}}

(1689)

将定义 Eqn. (1689) 应用于相同温度（无净能量交换）下热平衡中的两个黑色表面 i 和 j 会产生视角因子必须满足倒数关系的要求：

图 3. EQUATION_DISPLAY

{d F}_{i - j} d S_{i} = {d F}_{j - i} d S_{j}

(1690)

对于漫辐射，关系 Eqn. (1690) 适用于任何两个表面，无论其是否为黑色。

这些定义可以进一步应用于有限尺寸的表面，可通过对构成单元表面积分获得这些表面的视角因子。下图显示了两个有限表面之间的辐射交换：

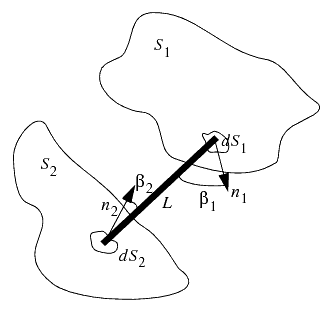
对于 (S1, S2) 对：

图 4. EQUATION_DISPLAY

F_{1 - 2} = \frac{\int_{S_{1}} \int_{S_{2}} {i^{'}}_{1} \frac{\cos (β_{1}) \cos (β_{2})}{π L^{2}} d S_{1} d S_{2}}{\int_{S_{1}} {i'}_{1} d S_{1}}

(1691)

并且（假定 $i'$ 为单元 1 上的常数）：

图 5. EQUATION_DISPLAY

F_{1 - 2} = \frac{1}{S_{1}} \int_{S_{1}} \int_{S_{2}} \frac{\cos (β_{1}) \cos (β_{2})}{π L^{2}} d S_{1} d S_{2}

(1692)

同样地：

图 6. EQUATION_DISPLAY

F_{2 - 1} = \frac{1}{S_{2}} \int_{S_{2}} \int_{S_{1}} \frac{\cos (β_{1}) \cos (β_{2})}{π L^{2}} d S_{1} d S_{2} or F_{2 - 1} = F_{1 - 2} \frac{S_{1}}{S_{2}}

(1693)

在 Simcenter STAR-CCM+ 中，边界表面离散为称作块的更小单元。这些块是连续边界网格单元格面的集合，并且会为每个块对计算视角因子。根据定义，块不会跨边界，因此其最多大至整个边界，或者小至边界网格单元面。每个块的表面上的发射功率（即，辐射强度）和辐射属性假定为均匀。

如上述方程Eqn. (1692) 和 Eqn. (1693) 中所示，视角因子完全为拓扑量，仅取决于两个表面的几何。但是，如果 Simcenter STAR-CCM+ 中存在部分透射和/或镜面反射表面，可能会引入对其他表面及其各自表面属性的进一步依赖。因此一般情况下，视角因子的集合取决于这些表面的表面几何以及各自的透射率和镜面反射率。对于固定几何和固定的表面透射率和镜面反射率，必须仅获得一次视角因子，通常在模拟开始时获得。

可使用光线跟踪法粗略估算二重积分。多边形集合表示表面，并且会使用角度求积离散立体角。对于每个表面或块，将通过计算域从块形心处开始跟踪预定义数量的光线。方向和权重基于块上理想半球体的离散化。

从一个块发出的光线可以执行以下任何操作：

碰到不透明块。
穿过半透明块（与碰撞块所属的边界的透射率成比例的强度降低）。
从镜面反射块反射。
穿过透明边界或开口，并在环境中离散。

在所有这些情况下，将在发射块与不透明块、半透明块、镜面反射块或环境之间生成视角因子。

与其他方法（半立方体、半球体或蒙特·卡罗）相比，此方法非常简单且经济高效。存在单位球体法的一些类比 [398]。光线跟踪完成后，获得的视角因子组分表可满足守恒，但是未满足倒数，因此需要执行后校正过程以强制应用倒数。也会强制应用守恒，因为施加倒数后，守恒将丢失。

以上常规定义用于描述两个独立表面之间无障碍的直接相互作用。实际上，当涉及更多表面时，从一个块发出的辐射能量在已经穿过一个或多个透明表面后，可以达到另一个块。辐射能量还可经受一个或多个镜面反射表面的反射。

S2S 辐射模型可用于对镜面透射（其中，从一个表面发射的辐射沿其原始方向穿透另一个表面）建模。下面为使用边界 $B_{1}$ 至 $B_{4}$ 和选定块对此情况的图示：

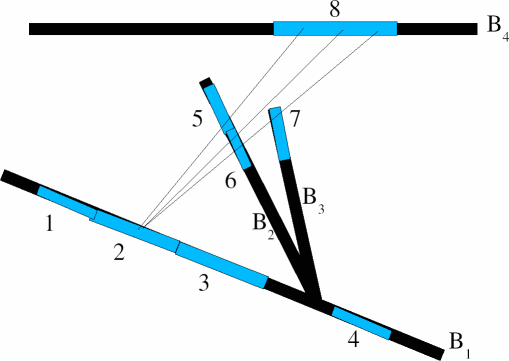
例如，要计算从 $B_{1}$ 上的块 2 到 $B_{4}$ 上的块 8 的辐射，需要对以下项求和：通过 5 直接到达 8 的能量、通过 6 直接到达 8 的能量以及通过 6 和 7 到达 8 的能量。每次辐射光线穿透表面时，该表面的透射率都会减弱其强度。因此，正确考虑所有可能的路径的唯一方式是在计算视角因子时考虑这些路径和透射率。该计算使用对较小的离散立体角的积分。

在光线跟踪过程中，将以类似方式考虑镜面反射表面的影响。当表面未达到完全反射时，镜面反射表面会改变光线的方向，并且可能改变光线强度。此外，表面可以同时为镜面反射和透射。在此特殊情况下，每条入射光线都会拆分成两条子光线 -- 一条穿透表面，另一条从表面反射。生成的两条子光线的强度由父光线的强度以及各自的镜面透射率和反射率确定。

当存在透射和/或镜面反射表面时，块对的视角因子为全局视角因子。这些全局视角因子已考虑两个块之间的空间中所有可能的辐射相互作用。全局视角因子不再只是拓扑量，并且在每次域中表面的透射率或镜面反射率发生变化时，必须重新计算这些因子。

环境块

当视角因子计算器检测到透明外部表面时，除了物理边界上的块以外，还会创建虚拟块。环境块是程序的内部块，并且可用于收集和考虑辐射到和辐射自区域周围的环境的所有能量。根据定义，环境块温度是热环境的辐射温度。

辐射平衡

在表面已分解为块并且已为块对计算视角因子后，将获得每个块上的辐射通量。通过对整个封闭表面组强制应用辐射平衡，可为每个辐射光谱或光谱波段单独获得辐射通量。

对于给定的辐射光谱或光谱波段 $λ$ ，可以根据入射、发射和透射的辐射表示每个块上的辐射效应，如下图的通用块 $i$ 所示。下图显示了块 i 上的辐射通量的示意图：

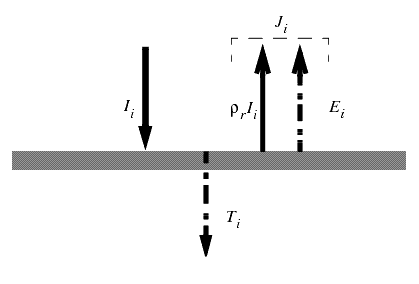
要在整个封闭表面组上平衡辐射，每个块接收的所有辐射必须来自其他块。通过对所有块求和，块 $i$ 上的总入射辐射为：

图 7. EQUATION_DISPLAY

Q_{I, i, λ} = S_{i} I_{i, λ} = \sum_{j = 1}^{N_{p}} \frac{F_{j-i, λ}}{(1 - τ_{i, λ} - ρ_{s, i, λ})} J_{d, j, λ} S_{j} + \frac{F_{e-i, λ}}{(1 - τ_{i, λ} - ρ_{s, i, λ})} J_{e, λ} S_{e}

(1694)

其中：

$S_{i}, S_{j}$ 分别为块 $i$ 和 $j$ 的表面积
$I_{i}$ 为块 $i$ [ $\frac{W}{m^{2}}$ ] 上的辐射或入射辐射通量
$N_{p}$ 为块总数
$F_{j-i, λ}$ 为块 $j$ 到 $i$ 的视角因子，通过使用光线跟踪依据方程Eqn. (1688) 到 Eqn. (1693) 的近似获得
$J_{d, j, λ}$ 为离开块 $j$ 的辐射通量的漫射分量，其有时称为热辐射
$F_{e -i, λ}$ 为环境块到块 $i$ 的视角因子
$τ_{i, λ}$ 为透射率
$ρ_{s, i, λ}$ 为反射率的镜面反射分量

视角因子包括任何透射或镜面反射表面的影响。相应地，可使用块 $i$ 处的表面属性的漫射部分： $(1 - τ_{i, λ} - ρ_{s, i, λ})$ 对视角因子进行有效标准化。

表面（可以为透射和/或镜面反射）之间视角因子的一般倒数关系为：

图 8. EQUATION_DISPLAY

F_{j-i, λ} = F_{i-j, λ} [\frac{S_{i} (1 - τ_{i, λ} - ρ_{s, i, λ})}{S_{j} (1 - τ_{j, λ} - ρ_{s, j, λ})}]

(1695)

通过在 Eqn. (1694) 中引入倒数关系，入射辐射通量为：

图 9. EQUATION_DISPLAY

I_{i, λ} = \sum_{j = 1}^{N_{p}} \frac{F_{i-j, λ}}{1 - τ_{j, λ} - ρ_{s, j, λ}} J_{d, j, λ} + \frac{F_{i-e, λ}}{1 - τ_{e, λ} - ρ_{s, e, λ}} J_{e, λ}

(1696)

其中， $J_{d, j, λ}$ 为漫射热辐射：

图 10. EQUATION_DISPLAY

J_{d, j, λ} = {ρ_{d, j, λ} I}_{j, λ} + E_{j, λ} + E_{d, j, λ}

(1697)

其中：

$E_{j, λ}$ 为基于普朗克定律的发射
$E_{d, j, λ}$ 为用户指定的非普朗克发射

在引入以下有效热辐射后：

图 11. EQUATION_DISPLAY

J_{i, λ}^{e f f} = \frac{J_{d, i, λ}}{1 - τ_{i, λ} - ρ_{s, i, λ}}

(1698)

辐射可以写为：

图 12. EQUATION_DISPLAY

I_{i, λ} = \sum_{j = 1}^{N_{p}} F_{i-j, λ} J_{j, λ}^{e f f} + F_{i-e, λ} J_{e, λ}^{e f f}

(1699)

块 $i$ 发射的总漫辐射为漫射反射分量和漫射发射分量之和：

图 13. EQUATION_DISPLAY

J_{d, i, λ} = ρ_{d, i, λ} I_{i, λ} + E_{i, λ} + E_{d, i, λ}

(1700)

对于每个块，将方程 Eqn. (1699) 和 Eqn. (1700) 相结合可产生 $J_{i, λ}^{e f f}$ 的方程：

图 14. EQUATION_DISPLAY

\begin{matrix} (1 - τ_{i, λ} - ρ_{i, λ}^{s}) (1 - F_{i-i, λ}) {J^{eff}}_{i, λ} - ρ_{d, i, λ} \sum_{(j = 1), (j \neq i)}^{N_{p}} [F_{i-j, λ} {J^{eff}}_{j, λ}] \\ = E_{i, λ} + E_{d, i, λ} + ρ_{d, i, λ} [F_{i-e, λ} (E_{env, λ} + J_{d, source, λ}) + J_{dir, source, λ}] \end{matrix}

(1701)

其中：

$J_{d, source, e}$ 为指定的外部漫辐射通量源，如太阳辐射
$J_{dir, source, i, λ}$ 为指定的外部直射通量源

要封闭方程组，可以进一步指定 Eqn. (1701) 右侧的发射能量和环境热辐射。对于任意光谱或波段，这些项定义如下。因此，这些定义适用于灰体模型或多波段光谱模型。在适当情况下，会注明灰体光谱模型（灰体热辐射）的简化。

给定光谱或波段的表面发射功率为该光谱或波段的发射率与黑体发射功率的乘积：

图 15. EQUATION_DISPLAY

E_{i, λ} = ε_{i, λ} Δ_{(λ_{1} \to λ_{2}, T_{i})} σ T_{i}^{4}

(1702)

其中：

$Δ_{(λ_{1} \to λ_{2}, T_{i})}$ 为光谱或波段的总黑体发射的分数
$λ_{1}$ 和 $λ_{2}$ 表示光谱或波段的波长下限和上限
$ε_{i, λ}$ 为发射率
$σ$ 为斯特藩-玻尔兹曼常数 [ $\frac{W}{m^{2} K^{4}}$ ]

下图显示了某波段的分数黑体发射：

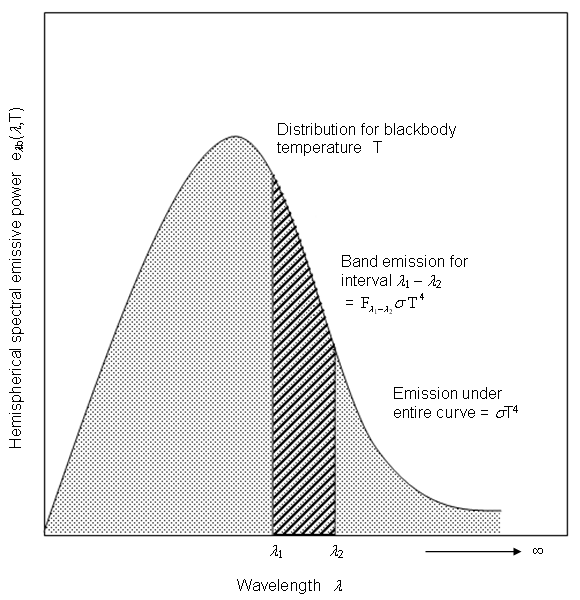
对于灰体辐射，波长边界实际上为零和无穷大，并且此因子其实为 1。对于多波段辐射，此分数为表面温度和波长边界的函数：

图 16. EQUATION_DISPLAY

Δ_{(λ_{1} \to λ_{2}, T)} = Δ_{(0 \to λ_{2}, T)} - Δ_{(0 \to λ_{1}, T)} = f (λ_{2} T) - f (λ_{1} T)

(1703)

通过对普朗克分布积分或者通过从基于此积分的表中插值，可以计算分数黑体发射函数 ([397])。

将使用发射率 1 以及零反射率和透射率将环境建模为黑体。因此，有效的环境热辐射为：

图 17. EQUATION_DISPLAY

J_{e, λ}^{e f f} = Δ_{(λ_{1} \to λ_{2}, T_{e})} σ T_{e}^{4}

(1704)

如之前一样，给定光谱或波段的总黑体发射分数取决于该光谱或波段的范围以及环境温度。对于灰体热辐射，该分数将减少为 1。

如果考虑太阳能负载，可能存在两个额外的源 — 太阳直射辐射和太阳漫辐射。出于根据光谱或波段划分这些负载的目的，假定通过太阳的平均表面温度下的黑体表示太阳发射的光谱分布。太阳直射通量和太阳漫射通量会增加环境的有效热辐射：

图 18. EQUATION_DISPLAY

{F_{i-e, λ} J}_{e, λ}^{e f f} = {F_{i-e, λ} [Δ_{(λ_{1} \to λ_{2}, T_{e})} σ T_{e}^{4} + Δ_{(λ_{1} \to λ_{2}, T_{s u n})} J_{d, solar, e}] + J}_{dir, solar, i, λ}

(1705)

此基于块的物理量取决于指定的太阳位置、指定的太阳直射通量和给定光谱波段的边界（用于划分总直射通量）。此物理量还取决于指定的光谱/波段透射率和模型几何。

通过将方程Eqn. (1702) 和 Eqn. (1705) 代入 Eqn. (1701) 并且展开 $i$ 到 $i$ 求和项，会产生有效热辐射的一般方程组：

图 19. EQUATION_DISPLAY

\begin{matrix} (1 - {τ_{i, λ} - ρ}_{s, i, λ}) (1 - F_{i-i, λ}) J_{i, λ}^{e f f} - ρ_{d, i, λ} \sum_{j = 1, j \neq i}^{N_{p}} F_{i-j, λ} J_{j, λ}^{e f f} \\ = ε_{i, λ} Δ_{(λ_{1} \to λ_{2}, T_{i})} σ T_{i}^{4} + E_{d, i, λ} \\ + ρ_{d, i, λ} {F_{i-e, λ} [Δ_{(λ_{1} \to λ_{2}, T_{e})} σ T_{e}^{4} + Δ_{(λ_{1} \to λ_{2}, T_{s u n})} J_{d, solar, e}] + J_{dir, solar, i, λ}} \end{matrix}

(1706)

对于灰体光谱模型，只存在一组方程，并且该组方程表示完整热光谱。对于多波段光谱模型，每个光谱波段都存在一个单独的方程组。在没有太阳辐射的情况下，将从 Eqn. (1706) 中省略太阳能负载项。

数值解

通过为构成每个块的所有边界面的网格单元面值计算表面平均值，可获得发射功率、反射率和透射率的块值：

图 20. EQUATION-DISPLAY

\begin{matrix} E_{i, λ} & = & ε_{i, λ} Δ_{(λ_{1} \to λ_{2}, T_{i})} σ T_{i}^{4} = \frac{\sum_{f_{1} (i)}^{f_{N} (i)} ϵ_{f_{k}, λ} Δ_{(λ_{1} \to λ_{2}, T_{f_{k}})} T_{f_{k}}^{4} S_{f_{k}}}{\sum_{f_{1} (i)}^{f_{N} (i)} S_{f_{k}}} \\ ρ_{i, λ} & = & \frac{\sum_{f_{1} (i)}^{f_{N} (i)} {ρ_{f_{k}, λ} S}_{f_{k}}}{\sum_{f_{1} (i)}^{f_{N} (i)} S_{f_{k}}} \\ τ_{i, λ} & = & \frac{\sum_{f_{1} (i)}^{f_{N} (i)} {τ_{f_{k}, λ} S}_{f_{k}}}{\sum_{f_{1} (i)}^{f_{N} (i)} S_{f_{k}}} \end{matrix}

(1707)

要保存能量，需要计算面发射功率的表面平均值而非单独计算面发射率和温度的平均值。给定整个块集合的发射功率和属性的情况下，将以矩阵形式由 S2S 求解器及其 AMG 线性求解器为每个光谱或波段求解辐射平衡方程组 Eqn. (1706)。

根据更新的有效热辐射值，可直接通过 Eqn. (1699) 获得块辐射通量。Eqn. (1699) 中对来自环境的辐射的效应基于 Eqn. (1704) 或 Eqn. (1705)，具体取决于是否考虑太阳能负载。然后，将使用 Eqn. (1698) 从有效热辐射中提取热辐射。在存在太阳辐射的情况下，这些通量包括太阳能负载的影响。

然后，从块通量衍生面上的辐射通量。每个面 f 处的辐射（入射通量）等于关联块 i 上的辐射。面热辐射为局部面发射功率和反射辐射的组合：

图 21. EQUATION_DISPLAY

\begin{matrix} I_{f, λ} = I_{i, λ} \end{matrix}

(1708)

图 22. EQUATION_DISPLAY

\begin{matrix} J_{f, λ} = E_{f, λ} + ρ_{f, λ} I_{i, λ} \end{matrix}

(1709)

上述方程中反射率为完全反射率（漫射 + 镜面反射）。要在之后从热辐射衍生净辐射通量时确保局部能量平衡，使用局部面发射功率而非块发射功率，这一点很关键。

通过对各个光谱或波段的通量求和，可计算完整热光谱：

图 23. EQUATION_DISPLAY

\begin{matrix} I_{f} = \sum_{λ \in s p e c t a}^{} I_{f, λ} \end{matrix}

(1710)

图 24. EQUATION_DISPLAY

\begin{matrix} J_{f} = \sum_{λ \in s p e c t r a}^{} J_{f, λ} \end{matrix}

(1711)

图 25. EQUATION_DISPLAY

{(q_{r})}_{f} = \sum_{λ \in s p e c t r a}^{} {(q_{r})}_{f, λ} = \sum_{λ \in s p e c t a}^{} [(1 - τ_{f, λ}) I_{f, λ} - J_{f, λ}]

(1712)

对于灰体光谱模型，求和运算无关紧要；灰体通量为总通量。对于多波段光谱模型，求和涉及所有光谱波段。Eqn. (1712) 用于定义边界的总净辐射热通量或完整光谱净辐射热通量（总吸收减去总发射）。正值表示边界的净吸收。

平均辐射温度 (MRT)

MRT 为热舒适性分析的有用变量，因为它提供“假想封闭空间的均匀温度，其中人体的辐射热传递等于实际非均匀封闭空间中的辐射热传递。”请参见 [401]。

通过使实际热通量与理想化热通量（即，均匀温度下且发射率为 1 时来自假想房间的热通量）相等，可衍生 MRT。通过代入相等热通量的表达式并进行重新排列，可根据辐射表示 MRT：

图 26. EQUATION_DISPLAY

{(T_{M R T})}_{f} = {(\frac{I_{f}}{σ})}^{\frac{1}{4}}

(1713)

上述表达式中的辐射或入射热通量为表面至表面求解的结果。此公式会考虑太阳辐射、来自热环境的辐射、透明表面的透射和非黑色表面的发射的潜在影响。