弹塑性材料

对于较小应变，应变张量可以写为：

其中，${\epsilon }_{el}$ 是弹性应变张量，${\epsilon }_{pl}$ 是塑性应变张量，${\epsilon }_{in}$ 包含对应变张量的任何非弹性影响（例如，热应变）。

根据 Eqn. (4503)，可以将应力张量写为：

其中，$D$ 为材料正切。因塑性变形而耗散的能量可以写为：

其中，$\sigma$ 为柯西应力张量。

塑性应变的标量度量为等效或累积塑性应变 ${\epsilon }_{eq}$。此物理量表示随着塑性损坏的增加而累积的增量塑性应变：

塑性应变的另一标量度量为有效的塑性应变 ${\epsilon }_{eff}$，定义为：

要描述弹塑性材料的应力应变曲线，可以定义称为塑势的函数，因此：

塑势是应力 $\sigma$ 和一些硬化变量 $\alpha$（请参见硬化模型）的函数。 $f=0$ 定义屈服面：

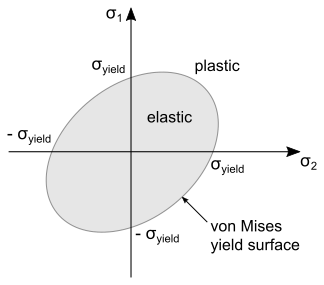
在 Eqn. (4520) 中，屈服表面之内的任何应力状态都是弹性的，屈服表面之外的任何应力都是塑性的。通常，屈服表面采用以下形式：

其中，${\sigma }^{*}$ 是一些应力度量，${\sigma }_Y$ 是材料屈服应力。对于金属，最常见的塑势为 J2 势（也称为 Von Mises 势），定义为：

硬化模型

硬化模型描述屈服表面如何随后续屈服而变化。例如，对于各向同性硬化，在尺寸扩展时，屈服表面会保持以同一位置为中心。

Simcenter STAR-CCM+ 提供了线性各向同性硬化和饱和硬化的标准模型，以及用户自定义的硬化模型。

Linear Isotropic Hardening(线性各向同性硬化)

此模型将屈服应力 ${\sigma }_Y$ 定义为等效塑性应变 ${\epsilon }_{eq}$ 的线性函数：

$$\begin{array}{c}{\sigma }_Y\left({\epsilon }_{eq}\right)\end{array}={\sigma }_{Y_0}+H_0{\epsilon }_{eq}$$

(4523)

其中，${\sigma }_{Y_0}$ 是初始屈服应力，$H_0$ 是定义线性函数斜率的硬化正切。

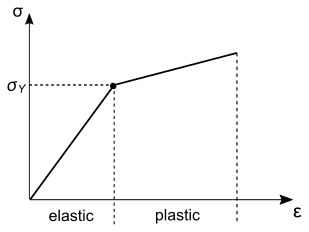
对于 $H_0=0$，屈服应力是常数 (${\sigma }_Y={\sigma }_{Y_0}$)。这种行为称为完全塑性。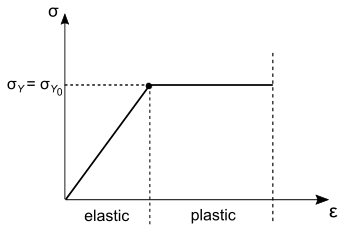

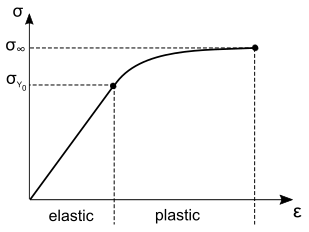
Saturation Hardening(饱和硬化)

此模型将屈服应力 ${\sigma }_Y$ 定义为 ${\epsilon }_{eq}$ 的非线性函数：

$$\begin{array}{c}{\sigma }_Y\left({\epsilon }_{eq}\right)\end{array}={\sigma }_{Y_0}+m\overline{H}{\epsilon }_{eq}+({\sigma }_{\infty }-{\sigma }_{Y_0})(1-e^{-\delta {\epsilon }_{eq}})$$

(4524)

其中， $m$ 、 $\overline{H}$ 、 ${\sigma }_{\infty }$ 和 $\delta$ 是可以通过曲线拟合材料测试数据找到的参数。Eqn. (4524) 给出的曲线接近应变较高时的渐进极限：

用户自定义

此模型可用于从实验数据中捕捉材料行为。要定义应力应变关系，需指定标称应力 $\sigma$ 及其相对于标称应变的导数 $\epsilon$ ：

$$\begin{array}{cc}\begin{array}{c}{\sigma }_Y\end{array};& \frac{\begin{array}{c}d{\sigma }_Y\end{array}}{d{\epsilon }_{eq}}\end{array}$$

(4525)

标称应变和标称应力表示未变形配置中的相应物理量：

$$\sigma =\frac{F}{A_0}$$

(4526)

$$\epsilon =\frac{\delta L}{L_0}$$

(4527)

这些标称测量值与较大变形的真实应力和应变值存在偏差，因此，此模型适用于变形较小的应用。