Contact with a Rigid Surface

A rigid contact constraint defines a boundary condition on the surface of a deformable solid. This boundary condition accounts for the contact between the solid and a rigid surface that is not part of the stress analysis.

Currently, Simcenter STAR-CCM+ allows you to model frictionless contacts with rigid planes.

Contact Pressure

Consider the interface $Γ_{C}$ between a deformable solid $s$ and a rigid plane $m$ .

The traction vector on $Γ_{C}^{s}$ (that is, the side of the interface belonging to the deformable solid) can be decomposed into its tangential and normal components:

T^{s} = T_{t}^{s} - P_{n}^{s} n

(4481)

where $T_{t}^{s}$ is the tangential Piola traction vector and $P_{n}^{s}$ is the nominal contact pressure relative to the initial, undeformed, contact surface $Γ_{C}^{s}$ [870]. The contact pressure $P_{n}^{s}$ is defined to be positive in compression.

For frictionless contacts, the only contribution to the traction vector comes from the normal component, that is, the contact pressure. The contact pressure on the initial surface is related to the pressure on the current, deformed, surface through:

P_{n}^{s} = j^{s} p_{n}^{s}

(4482)

where $p_{n}^{s}$ is the contact pressure relative to the current surface $γ_{C}^{s}$ and $j$ is the jacobian that relates the initial and current surfaces:

j^{s} = \frac{d γ_{C}^{s}}{d Γ_{C}^{s}}

(4483)

The contact conditions in the normal direction can be formulated as a Karush-Kuhn-Tucker condition [870]. For each point on the contact surface $Γ_{C}^{s}$ :

{\begin{cases} P_{n}^{s} \geq 0 \\ g_{n} \geq 0 \\ P_{n}^{s} g_{n} = 0 \end{cases}

(4485)

where $g_{n}$ is the contact gap function that defines the distance between a point on the solid body surface and its projection on the rigid obstacle surface.

Contribution of the Contact Pressure to the Virtual Work

For frictionless contacts, only the contact pressure contributes to the virtual work equation for the deformable solid (Eqn. (4464)), which becomes:

\begin{matrix} δ Π & = & \int_{V_{0}} δ u \cdot ρ_{0} \ddot{u} d V - \int_{V_{0}} δ u \cdot b d V + \int_{V_{0}} δ E : S d V \\ - & \int_{Γ_{τ}} δ u \cdot \bar{τ} d Γ - \int_{Γ_{C}^{s}} P_{n}^{s} δ g_{n} d Γ^{s} = 0 \end{matrix}

(4486)

where the last term on the left-hand side is the contact contribution. The variation of the contact gap $δ g_{n}$ is given by:

δ g_{n} = δ u^{s} \cdot \bar{n}

(4487)

where $\bar{n}$ is the surface normal pointing out of the rigid surface.

Penalty Method for Contact Enforcement

Simcenter STAR-CCM+ models the relationship between the contact pressure and the gap function using the penalty method. The penalty method models the hard contact by penalizing any nonphysical penetrations of the solid body into the rigid surface.

With this approach, the $P_{n}^{s}, g_{n}$ relationship is defined as:

P_{n}^{s} = - ϵ {〈 g_{n} 〉}_{-}

(4488)

where ${〈 g_{n} 〉}_{-}$ is defined as:

{〈 g_{n} 〉}_{-} = {\begin{matrix} 0 & \forall g_{n} \geq 0 \\ {\begin{matrix} g \end{matrix}}_{n} & \forall g_{n} < 0 \end{matrix}

(4489)

and $ϵ$ is a parameter that penalizes the nonphysical penetrations. With Eqn. (4488), the contact contribution in Eqn. (4486) can be written as:

\int_{Γ_{C}^{s}} P_{n}^{s} δ g_{n} d Γ^{s} = - \int_{Γ_{C}^{s}} δ g_{n} ϵ {〈 g_{n} 〉}_{-} d Γ^{s}

(4490)

The penalty method describes a perfectly rigid contact only for $ϵ \to \infty$ . Any finite value introduces a modeling error. However, too large values can impair the convergence of the numerical schemes. Therefore, the penalty parameter value must be chosen as a compromise between modeling accuracy and numerical stability. The optimal value of $ϵ$ is related to the stiffness of the solid material and the mesh size:

ϵ \propto \frac{E}{h}

(4491)

where $E$ represents the material stiffness and $h$ is the numerical accuracy, that is, the finite element's size.

Uzawa Algorithm for Contact Enforcement

To reduce the influence of the penalty parameter on the solution accuracy, the Uzawa algorithm combines the penalty method with the Lagrange Multiplier Method. The Uzawa algorithm is an Augmented Lagrangian method that introduces Lagrangian multipliers (

λ

) for the constraint enforcement. Eqn. (4488) is extended to:

P_{n}^{s} = - {〈 λ + ϵ g_{n} 〉}_{-}

(4492)

Introducing Lagrange variables to the contact pressure can lead to an increase in the number of degrees of freedom in the finite element scheme. However, for the Uzawa algorithm, this is avoided by considering the Lagrange multipliers as a fixed variable while solving the finite element system. To provide the optimal Lagrange multipliers for each Newton iteration, they are updated in a separate fixed point scheme:

λ^{*} = {〈 λ^{(k)} + ϵ g_{n}^{(k)} 〉}_{-}

(4493)

where $λ^{*}$ is the current contact pressure ( $λ^{*} = λ^{(k + 1)}$ ). The fixed point scheme is updated until the impenetrability condition ( $g_{n} \geq 0$ ) is satisfied.

As the convergence of the Uzawa algorithm is influenced by the penalty parameter, the adaptive penalty scheme can be used to automatically increment the penalty parameter in case the maximum penetration does not decrease sufficiently.

ϵ^{(k + 1)} = {\begin{matrix} 10 ϵ^{(k)} & \forall | g_{n}^{(k)} | > \frac{1}{4} | g_{n}^{(k - 1)} | \\ ϵ^{(k)} & \forall | g_{n}^{(k)} | \leq \frac{1}{4} | g_{n}^{(k - 1)} | \end{matrix}

(4494)

To ensure the contact conditions have been met with sufficient accuracy and to halt the Uzawa augmentation, the contact pressure and the violation of the contact conditions (contact constraint) are monitored:

P_{t o l} \geq \frac{‖ λ^{*} - λ^{(k)} ‖}{c_{λ}}

(4495)

g_{t o l} \geq \frac{1}{l_{r e f}} ‖ {〈 g_{n}^{(k)} 〉}_{-} ‖

(4496)

where $c_{λ}$ is the normalization factor and $l_{r e f}$ is the reference length, currently $l_{r e f} = 1$

Discretization of the Rigid Contact Gap

To calculate the contribution of the contact to the virtual work of the system,

δ Π^{c}

, the contact gap is discretized in combination with the penalty method:

δ Π^{c} = \int_{Γ_{C}^{s}} P_{n}^{s} δ g_{n} d Γ^{s}

(4497)

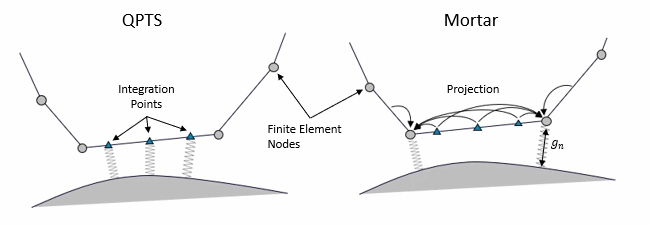
Quadrature Point to Surface scheme (QPTS): The quadrature point to surface scheme (QPTS) computes the exact contact gap for the finite element integration points using Gaussian integration, and applies the penalty method directly to the contact gap values for the integration points:

$δ Π^{c} \approx - \sum_{q} δ g_{n} (ξ_{q}^{s}) ϵ {〈 g_{n} (ξ_{q}^{s}) 〉}_{_} w_{q}$

(4498); where $ξ_{q}^{s}$ and $w_{q}$ are the local coordinates and weights of the integration points of the numerical integration rule.
Mortar: In contrast, the Mortar discretization introduces a finite element discretization of the contact pressure:

$P_{n}^{s} \approx \sum_{i} N_{i}^{p} P_{i}^{s}$

(4499); where $N_{i}^{p}$ are the finite element shape functions and $P_{i}^{s}$ are the nodal contact pressures.; To provide the discrete contact gap, the contact gap is projected onto the same discretization as the contact pressure:

${\hat{g}}_{i} = \frac{1}{A_{i}} \int_{Γ^{s}} N_{i}^{p} g_{n} d Γ$

(4500); where $A_{i}$ is the nodal tributary area:

$A_{i} = \int_{Γ s} N_{i}^{p} d Γ$

(4501); The penalty method is then applied to the discretized contact gap to express the nodal contact pressure as a function of the discretized contact gap ( $P_{i}^{s} = - ϵ {〈 {\hat{g}}_{i} 〉}_{_}$ ) to produce the contact virtual work term:

$δ Π^{c} \approx \sum_{i} P_{i}^{s} A_{i} δ {\hat{g}}_{i} = - \sum_{i} ϵ {〈 {\hat{g}}_{i} 〉}_{_} A_{i} {\hat{g}}_{i}$

(4502)