应力

应力是作用于表面的单位面积力的度量。在固体结构中，外力或温度变化会引起可能导致固体结构运动和变形的应力场。而阻碍结构变形的内力也会引起可将结构恢复到原始未变形状态的内部弹性应力。一些材料还具有内置应力，这种应力在没有作用力和变形时就已存在。

一般情况下，作用于体的平面截面上的应力由矢量 $τ$ （称作应力矢量或拉力）定义如下：

图 1. EQUATION_DISPLAY

τ = (\begin{matrix} τ_{x} \\ τ_{y} \\ τ_{z} \end{matrix}) = (\begin{matrix} F_{x} / A \\ F_{y} / A \\ F_{z} / A \end{matrix})

(4432)

其中， $F$ 为作用于平面的力， $A$ 为平面的面积。

由于应用力的面积接近零，因此某点处的应力是单位面积上的力。在点处，存在体的无穷多个平面截面。但是，该点处的应力状态完全由与三个通过该点且相互垂直的平面关联的应力矢量定义。因此，任何平面上的任何点处的应力状态均通过以下形式的二阶张量定义：

图 2. EQUATION_DISPLAY

σ = (\begin{matrix} {\begin{matrix} σ \end{matrix}}_{x x} & {\begin{matrix} σ \end{matrix}}_{x y} & {\begin{matrix} σ \end{matrix}}_{x z} \\ {\begin{matrix} σ \end{matrix}}_{y x} & {\begin{matrix} σ \end{matrix}}_{y y} & {\begin{matrix} σ \end{matrix}}_{y z} \\ {\begin{matrix} σ \end{matrix}}_{z x} & {\begin{matrix} σ \end{matrix}}_{z y} & {\begin{matrix} σ \end{matrix}}_{z z} \end{matrix})

(4433)

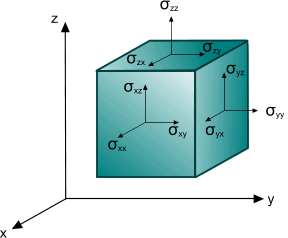
由于力矩的总和必须在体的体积收缩至零时归零，因此应力张量是对称的。

非对角项称为剪切应力，因为其作用方向与面相切。对角项称为法向应力，因为其作用方向与面垂直。

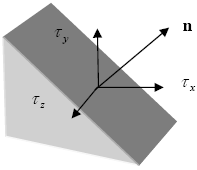
平面上的应力矢量可表示为矩阵积：

图 3. EQUATION_DISPLAY

τ = σ \cdot n = (\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}) (\begin{matrix} n_{x} \\ n_{y} \\ n_{z} \end{matrix})

(4434)

其中，

n

为垂直于平面的单位矢量。

应力的简单状态包括：

体积应力 - 整个材料中的应力在所有方向上均相同。
平面应力 — 平表面上无负载的薄体材料处于平面应力状态，即，垂直于平表面的方向上的应力为零（例如，如果平表面位于 x-y 平面上，则 z 方向上的应力为零， $σ_{z z} = σ_{x z} = σ_{y z} = 0$ ）。
单轴应力 - 只有一个应力分量不为零，例如 $σ_{x x} \neq 0, σ_{y y} = σ_{z z} = σ_{x y} = σ_{y z} = σ_{z x} = 0$ 。
双轴应力 - 只有两个轴分量不为零，例如 $σ_{x x} \neq 0 σ_{y y} \neq 0, σ_{z z} = σ_{x y} = σ_{y z} = σ_{z x} = 0$ 。
剪切应力 - 除沿 x、y 和 z 轴的应力分量外均非零。

应力定义

可以通过各种方法定义应力。例如，可以在未变形配置或变形配置中定义它。对于无限小应变（请参见 Eqn. (4444)），未变形配置与变形配置等效。

柯西应力: Eqn. (4433) 中的应力张量在变形配置中定义，并且更正式地称为柯西应力或真应力。柯西应力是当前配置中作用于体任何表面的拉力的直接度量。对于输出，Simcenter STAR-CCM+ 使用柯西应力。
第二皮奥拉-基尔霍夫应力: 第二皮奥拉-基尔霍夫应力张量 $S$ 定义为：; 图 4. EQUATION_DISPLAY

$S = \det (F) F^{- 1} σ F^{- T}$
(4435); 其中， $σ$ 为柯西应力， $F$ 为 Eqn. (4428) 中的变形梯度张量。
主应力: 在固体的任何点上，始终有三个平面，称为主平面，这些平面上的剪切应力（即应力矢量的切向分量）为零。与这些平面关联的应力矢量由以下公式给出：
图 5. EQUATION_DISPLAY

$s_{k} = s_{k} n_{k}$
(4436)

其中， $i = 1, 2, 3$ 的 $n_{k}$ 表示主平面法向， $s_{k}$ 表示 $σ$ 的特征值（请参见 Eqn. (5209)）。 $σ$ 的特征值称为主应力，其中 $s_{1}$ 为最大主应力， $s_{3}$ 为最小主应力， $s_{2}$ 为中间主应力，并且 $s_{1} \geq s_{2} \geq s_{3}$ 。; 如果材料处于静水应力状态，则所有主应力相等。; 固体力学使用以下约定：应力在受拉时为正，在受压时为负，因此最大主应力为拉应力。因此，它通常用来度量材料中的拉伸失效。
最大剪切应力: 在一个平面上，剪切应力为最大主应力。最大剪切应力是与塑性行为关联的韧性失效的重要度量。定义如下：
图 6. EQUATION_DISPLAY

$τ_{\max} = \frac{(s_{1} - s_{3})}{2}$

(4437)

其中， $s_{1}$ 和 $s_{2}$ 由 Eqn. (4436) 给出。
平均应力: 平均应力或压力定义为：
图 7. EQUATION_DISPLAY

$σ_{m} = p = \frac{1}{3} t r (σ) = \frac{(s_{1} + s_{2} + s_{3})}{3}$

(4438); 如果材料处于静水应力状态，则平均应力解释为压力的负值。
偏应力: 偏应力可用于描述塑性屈服和韧性失效。定义如下：
图 8. EQUATION_DISPLAY

$σ^{d} = σ - σ_{m} I$

(4439)
von Mises 应力: von Mises 应力是很重要的韧性失效度量。它表示偏应力的大小，与平均应力无关：
图 9. EQUATION_DISPLAY

$σ_{v m} = \sqrt{\frac{1}{2} ({(s_{1} - s_{2})}^{2} + {(s_{1} - s_{3})}^{2} + {(s_{2} - s_{3})}^{2})}$

(4440); 如果材料处于单轴应力状态，则 von Mises 应力等于应力的非零分量。通常，通过加载大致处于单轴应力状态的试样来研究材料屈服。