电动势模型

在低频电动应用场景中，Simcenter STAR-CCM+ 根据电势计算由电场的非旋转分量引发的电流密度。

电动势方程

Simcenter STAR-CCM+ 提供多种电势计算方法。第一种方法通常适用于所有电动应用场景，而第二种方法特定于具有单谐波时间相关性的电势（请参见谐波时间依赖性）。

电动势

Simcenter STAR-CCM+ 根据以下公式计算电势：

图 1. EQUATION_DISPLAY

- \oint_{A}^{} σ \nabla ϕ \cdot d a - \oint_{A}^{} σ \frac{\partial A}{\partial t} \cdot d a = - \oint_{A}^{} σ ρ_{ϵ} \cdot d a + \int_{V}^{} S_{ϕ} d V

(4277)

上述公式通过对 Eqn. (4242) 进行网格单元域积分获得。Simcenter STAR-CCM+ 使用有限体积法对 Eqn. (4277) 进行离散和求解。

左侧第二项表示由随时间变化的磁场引发的涡流。Simcenter STAR-CCM+ 根据 Eqn. (4241) 计算此项。如果 Simcenter STAR-CCM+ 不求解磁矢势，则方程中不包含此项。

谐波平衡 Fv 电动势

对于具有单谐波时间相关性的势，Simcenter STAR-CCM+ 基于下式计算复电势：

图 2. EQUATION_DISPLAY

\begin{matrix} \oint_{A} (σ^{"} \nabla ϕ^{"} - σ^{'} \nabla ϕ^{'}) \cdot d a + {ω_{0} \oint}_{A}^{} (σ^{'} A^{"} + σ^{"} A^{'}) \cdot d a = \int_{V}^{} S_{ϕ}^{'} d V \\ - \oint_{A} (σ^{'} \nabla ϕ^{"} + σ^{"} \nabla ϕ^{'}) \cdot d a - {ω_{0} \oint}_{A}^{} (σ^{'} A^{'} - σ^{"} A^{"}) \cdot d a = \int_{V}^{} S_{ϕ}^{"} d V \end{matrix}

(4278)

上述公式通过对 Eqn. (4267) 进行网格单元域积分获得。Simcenter STAR-CCM+ 使用有限体积法对 Eqn. (4278) 进行离散和求解。与 Eqn. (4277) 不同（求解时可以忽略电势的影响），Eqn. (4278) 始终与谐波磁矢势方程 Eqn. (4307) 一起求解。

源项

Eqn. (4277) 和 Eqn. (4278) 右侧的源项表示流过边界表面 $A$ 的电流。

Eqn. (4277) 和 Eqn. (4278) 的右侧通常为零。但是，为了顾及未求解的物理量，Simcenter STAR-CCM+ 提供两个用户自定义源，即转移电流密度（在 Eqn. (4278) 中为复量）和电动势密度（仅适用于 Eqn. (4277)）。 $S_{ϕ}$ $ρ_{ϵ}$

在 Eqn. (4242) 中，这些项隐式包含在项 $\nabla\cdot J_{e x}$ 中。

电流密度的额外源可对 Eqn. (4277) 有贡献，例如，运动中的导电流体引发的电流密度。这些效应将在特定的章节中介绍。

边界和交界面条件

在域边界处，求解必须满足定义电势 $ϕ$ 的狄利克雷边界条件，或者满足定义与边界垂直的电势梯度 $\nabla ϕ$ 分量的诺伊曼边界条件。以下实现会应用于电势 (Eqn. (4277)) 和复电势 (Eqn. (4278))。对于复电势，边界和交界面处指定的物理量通常十分复杂。

在边界面 $Γ$ 处，狄利克雷边界条件实施如下：

图 3. EQUATION_DISPLAY

ϕ_{Γ} = ϕ_{0} - \frac{ϕ_{0} - \bar{ϕ}}{R^{0} + R^{e x}} R^{0}

(4279)

其中，

ϕ_{0}

为面相邻网格单元形心处的电势值，

\bar{ϕ}

为用户自定义电势。电阻

R^{0}

定义如下：

图 4. EQUATION_DISPLAY

R^{0} = \frac{s \cdot n}{σ a}

(4280)

其中， $n$ 为面网格面积矢量， $s$ 为网格单元面和网格单元形心之间的矢量， $σ$ 为材料的导电率。 $R^{ex}$ 用于顾及其他电阻源。如果 $R^{e x} = 0$ ，则 Eqn. (4279) 简化为基本的狄利克雷边界条件，用于指定边界处的电势值 $ϕ_{Γ} = \bar{ϕ}$ 。

可在交界面处指定相同的条件：

图 5. EQUATION_DISPLAY

\begin{matrix} ϕ_{Γ_{0}} = & ϕ_{0} - \frac{ϕ_{0} - ϕ_{1}}{R^{0} + R^{e x} + R^{1}} R^{0} = ϕ_{0} - J_{n_{0}} R^{0} \\ ϕ_{Γ_{1}} = & ϕ_{1} - \frac{ϕ_{1} - ϕ_{0}}{R^{0} + R^{e x} + R^{1}} R^{1} = ϕ_{1} - J_{n_{1}} R^{1} \end{matrix}

(4281)

其中下标 0 和 1 表示边界 0 和边界 1（即，交界面的两侧）。接触交界面处的电流所耗散的能量对能量方程没有任何影响，除非对焦耳加热或热电现象进行显式建模。请参见焦耳加热和热电。

对于诺伊曼边界条件，可通过指定以下任一项定义

\nabla ϕ

的法向分量：

电流密度 $J$ （请参见 Eqn. (4228)）
通过 $Γ$ 的总电流，即：
图 6. EQUATION_DISPLAY

$I_{Γ} = {- \oint}_{Γ} J \cdot d a$
(4282)
单位电流 $J_{n}$ ，即 $J$ 与 $Γ$ 垂直的分量：
图 7. EQUATION_DISPLAY

$J_{n} = - J \cdot n$
(4283)

其中， $n$ 为边界表面法向。负值 $J_{n}$ 表示电流密度朝向边界表面法向方向（即， $J_{n} = - J \cdot n < 0$ ）。
伏安特性，用于定义表示流过边界的电流与边界处的电势之间关系的 I-V 曲线。在电化学应用中，这种关系通常使用 Butler-Volmer 方程定义。有关更多信息，请参见Butler-Volmer 电流电势特性。

还可以在交界面处指定伏安特性、总电流和单位电流。对于单位电流，符号约定与诺伊曼边界相同，区别在于源的符号始终根据边界 0 选择。

将其他电阻源应用于边界或交界面时，比电阻率定义为：

R^{e x} = R^{0} A_{Γ} = R^{0} [A_{Γ_{1}} + A_{Γ_{2}} + ...]

(4284)

R^{e x} = R^{0} \int_{Γ}^{} a d Γ = R^{0} [\int_{Γ_{1}}^{} a_{1} d Γ_{1} + \int_{Γ_{2}}^{} a_{2} d Γ_{2} + ...]

(4285)

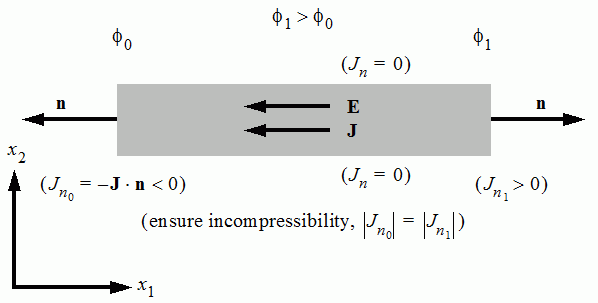
其中为表面积，而为对边界或交界面积分的单位面积。 $A$ $a$ $Γ$

当接触区域指定为单个表面时（这在它们彼此至少共享一条边的大多数情况下是合理的）：

Γ_{1} \cap Γ_{2} \neq \emptyset

(4286)

在这种情况下，比电阻率定义为：

R^{e x} = R^{0} [A_{Γ_{1}} + A_{Γ_{2}}]

(4288)

(4287)

作用于和的阻力分布定义为：

Γ_{1}

Γ_{2}

R_{Γ_{1}}^{0} = \frac{R^{e x}}{A_{Γ_{1}} + A_{Γ_{2}}}, R_{Γ_{2}}^{0} = \frac{R^{e x}}{A_{Γ_{1}} + A_{Γ_{2}}}

(4289)

因此，经过的总电流等于：

Γ

I_{t o t} = \int_{Γ_{1}}^{} J \cdot n d a_{Γ_{1}} + \int_{Γ_{2}}^{} J \cdot n d a_{Γ_{2}}

(4290)

或者，如果接触区域指定为相互独立：

Γ_{1} \cap Γ_{2} = \emptyset

(4291)

比电阻率定义为：

R_{Γ_{1}}^{e x} = R^{0} A_{Γ_{1}}, R_{Γ_{2}}^{e x} = R^{0} A_{Γ_{2}}

(4292)

而作用于和的阻力分布定义为：

Γ_{1}

Γ_{2}

R_{Γ_{1}}^{0} = \frac{R_{Γ_{1}}^{e x}}{A_{Γ_{1}}}, R_{Γ_{2}}^{0} = \frac{R_{Γ_{2}}^{e x}}{A_{Γ_{2}}}

(4293)

因此，经过和的总电流等于：

Γ_{1}

Γ_{2}

I_{Γ_{1}} = \int_{Γ_{1}}^{} J \cdot n d a_{Γ_{1}}, I_{Γ_{2}} = \int_{Γ_{2}}^{} J \cdot n d a_{Γ_{2}}

(4294)