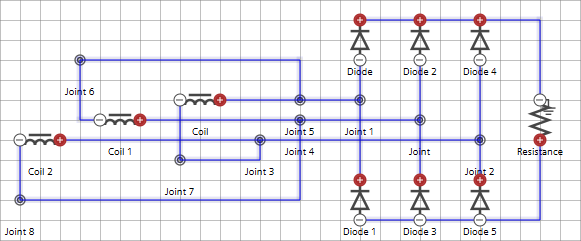
励磁线圈：场-路耦合

电路侧

假设场模拟域中存在 $N$ 个线圈。这些线圈中每个线圈的电流 $I_r$ （其中 $r=1,\dots ,N$ ）均形成一个电流矢量 $\mathbf{I}=(I_1,\dots ,I_N)$ 。同样，每个线圈端子的压差 $V_r$ 均可用一个矢量 $\mathbf{V}=(V_1,\dots ,V_N)$ 来描述。在电路中，对感应电流和电机旋转的响应可通过以下方程来表示：

其中， $\mathbf{R}$ 为直流电阻。 $\mathbf{R}$ 可以使用为励磁线圈模型所选的区域的特殊报告来计算。第一行是计算磁链 $\mathbf{\Psi }$ 时间导数的直接方法，实际上是使用特定电动势的体积积分报告提供的。但是，对于某些机型，使用这种方法捕捉运动相关性在数值上可能不稳定。

提取方程第二行中的参数应该能解决这些问题。这些参数在微分电感矩阵 ${\mathbf{L}}^{\partial \mathbf{I}}$ 中。这通常是一个满秩矩阵，根据相应线圈对的邻近位置，有些输入项接近于 0。最后一项 ${\partial }_{\theta }\mathbf{\Psi }{\theta }^{\prime }\left(t\right)$ 是指运动感应电压。有关提取方法，请参见 [850] 的第 3 章。

由于电感矩阵是一个满秩矩阵，因此需要表示为多连接组件，而不是电流双极电路元件。

场侧

基于静磁近似（在其中所有载流区域都是绞合导线）的瞬态模拟在适当的边界条件下求解以下模型，如下所述：

其中：

• $v\left(\mathbf{A}\right)$ 为材料渗透率的倒数。
• $\mathbf{J}$ 为电流密度分布，由导体的形状和电路状态决定。

Eqn. (4380)，离散化时，会导致 $\mathbf{a}$ 与右侧 $\mathbf{b}$ 中表示的电流或其他源的非线性方程。

使用 Eqn. (4379) 中最后两个求和，可以求解上述方程的多个线性化方程组。

电感矩阵

电感矩阵 ${\mathbf{L}}^{\partial \mathbf{I}}$ 描述了系统磁链相对于电流更改的变化。对于其导数，转子位置被视为固定。

电路和场之间的基本数据交换在场侧通过有限元励磁线圈模型完成，在电路侧通过集总参数模型完成。

Eqn. (4381) 的右侧是矢量的线性组合，其中每个矢量表示一个单独的励磁线圈 $\mathbf{b}=\sum _{i=1}^N{w}_i{I}_i$ 。

Eqn. (4381) 的求解应用迭代过程使残余 $r\left(\mathbf{a}\right)=M\left(\mathbf{a}\right)\mathbf{a}-\mathbf{b}$ 降为零，方法是使用以下方程

$$r(\mathbf{a}+\delta \mathbf{a})-r\left(\mathbf{a}\right)=JR\left(\mathbf{a}\right)\delta \mathbf{a}$$

(4382)

$r(\mathbf{a}+\delta \mathbf{a})\approx 0$ ，因此 $-r\left(\mathbf{a}\right)=JR\left(\mathbf{a}\right)\delta \mathbf{a}$ 。

这还可用于度量 ${\mathbf{a}}^{*}$ 的偏差，作为对右侧 ${\mathbf{b}}^{*}+\delta \mathbf{b}$ （作为由以下方程给定的一阶扩展）中微小信号变化的反应：

$$M({\mathbf{a}}^{*}+\delta \mathbf{a})=M\left({\mathbf{a}}^{*}\right){\mathbf{a}}^{*}+J\left({\mathbf{a}}^{*}\right)\delta \mathbf{a}=\mathbf{b}+\delta \mathbf{b}$$

(4383)

此外，可以通过求解 $JR\left({\mathbf{a}}^{*}\right)\delta \mathbf{a}=\delta \mathbf{b}$ 来计算右侧的更改一阶反应。

返回系统的磁链（这是给定励磁线圈求解中的线性映射）后，将设置右侧的方差以表示励磁线圈中作用电流的微小变化 $\delta {\mathbf{b}}_i=w_i\delta I_i$ ：

$$\delta {\psi }_r=\underset{j}{\mathrm{\Sigma }}{w}_r\delta {\mathbf{a}}_j=\underset{j}{\mathrm{\Sigma }}{w}_r{J}^{-1}\left({\mathbf{a}}^{*}\right)\delta {\mathbf{b}}_j=\underset{j}{\mathrm{\Sigma }}\left[w_r{J}^{-1}\left({\mathbf{a}}^{*}\right)w_j\right]\delta I_j$$

(4384)

请注意 $w_r{J}^{-1}\left({\mathbf{a}}^{*}\right)w_j=L_{rj}^{\partial }\left({\mathbf{a}}^{*}\right)$ 。

因此，获取感应矩阵分量需要求解不同右侧的雅可比，然后将结果乘以线圈磁链 $r$ 的加权矢量 $w_r$ 。

对于电机，属于一个相的线圈可以收集在磁链报告中。这通常意味着求解三个相并获得 3x3 电感矩阵。

对于异步机器，求解还必须考虑转子笼中的感应电流。

电动势

电动势的模拟需要获得线圈磁链因旋转而发生的变化。必须计算线圈电流的扭矩变化。扭矩 $T\left(\mathbf{a}\right)$ 是以下场函数的简单圆柱表面积分：

$$E_r=\frac{T\left({\mathbf{a}}^{*}\right)-T(a^{*}+\lambda \delta \mathbf{a}{|}_{\delta \theta =0})}{\lambda \delta I_r},\lambda =\kappa \frac{\Vert {\mathbf{a}}^{*}\Vert }{\Vert \delta \mathbf{a}\Vert }$$

(4385)

$\kappa$ 是建议范围为 0.01 到 0.05 的小参数。因此线圈的解 $\delta a_i$ 经过两次后处理。

总结和潜在用户体验

通过对附加右侧使用非线性解算方案的雅可比矩阵，在 Simcenter STAR-CCM+ 中计算感应矩阵。然后，可以指定线圈的连接以形成相，并因此减少感应矩阵电路元件中的极点对数量：

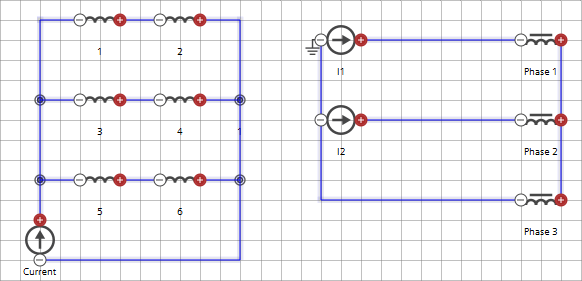
为此，可以先定义感应矩阵元件，然后执行添加一组相连线圈的操作。每一线圈组最终都定义了一个极点对。例如，对于上述电路，一个组连接线圈 1 和 2 形成相 $u$ ，以此类推。

对于运动情况，还需要一个元件：每个相脚的运动感应电压必须添加到每个接触对。