本构关系

介电常数和磁导率

电场 $E$ 和电通量密度 $D$ 以及磁场 $H$ 和磁通量密度 $B$ 之间的本构关系可以概括为：

其中，介电常数 $\epsilon$ 描述材料响应电场的行为，磁导率 $\mu$ 描述材料响应磁场的行为。磁导率的倒数称为磁阻率 $\nu ={\mu }^{-1}$ 。

对于除铁电体和铁磁体以外的材料，Eqn. (4219)和Eqn. (4220)近似线性。

通常， $\epsilon$ 和 $\mu$ 由二阶张量表示，分别定义矢量 $D$ - $E$ 和 $H$ - $B$ 之间的线性转换。

例如，对于 3D 域，Eqn. (4219)的矩阵形式为：

或者，对于 x-y 平面上的 2D 域，可以写为：

对于均匀材料， $\epsilon$ 和 $\mu$ 分量与材料内的位置无关。对于不均匀材料，这些分量是位置的函数。

在各向同性材料的特殊情况下， $\epsilon$ 和 $\mu$ 将简化为对角矩阵，其中，对角分量 ${\epsilon }_{11}={\epsilon }_{22}={\epsilon }_{33}=\epsilon$ 且 ${\mu }_{11}={\mu }_{22}={\mu }_{33}=\mu$ ，因此可以使用标量进行定义。具体地说， $\epsilon$ 可以相对于真空介电常数 ${\epsilon }_0=8.85\times {10}^{-12}[F/m]$ 定义，因为 $\epsilon ={\epsilon }_r{\epsilon }_0$ ，其中 ${\epsilon }_r$ 称为相对介电常数。 $\mu$ 可以根据真空磁导率定义， ${\mu }_0=4\pi \times {10}^{-7}\left[H/m\right]$ ，当 $\mu ={\mu }_r{\mu }_0$ ，其中 ${\mu }_r$ 称为相对磁导率。对于顺磁性材料， $\mu >{\mu }_0$ ，而反磁性材料则显示 $\mu <{\mu }_0$ 。

铁磁材料显示对应用的电磁场做出非线性响应。对于此类材料，Eqn. (4220)将变为非线性函数方程[848]：

通常，温度变化可能影响铁磁材料和顺磁材料的磁导率。通常，建议通过磁化率 $\chi$ 表示 $\mu$ 与温度的依赖性，定义如下：

$\chi$ 对温度的依赖性可以近似如下：

其中， ${\chi }_{ref}\left(H\right)$ 为环境温度 ( $T_{ref}=20C^{\circ }$ ) 下的磁化率， $S\left(T\right)$ 为磁化率温度因子， $S\left(T_{ref}\right)=1$ 。

铁磁材料常用于电动机等电气设备。铁磁材料的 $B$ - $H$ 曲线或磁滞回线具有以下形式：

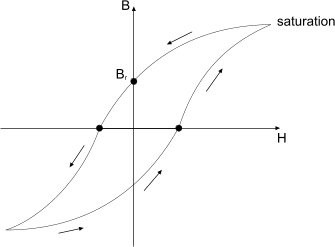
该图显示了磁化过程（ $B$ 随 $H$ 而增加，直至材料达到饱和）和消磁过程（ $B$ 随 $H$ 而降低，直至材料达到（反向）饱和）。当应用的磁场为零（即， $H=0$ ）时，磁通量密度 $B_r$ 为非零的材料称为永磁。 $B_r$ 称为剩余磁通量密度。

对于在 $B\text{-}H$ 特性的第一象限中运行的线性材料和软质材料，存储在磁场中的能量密度定义如下：

对于线性材料，该能量密度等于共能密度，定义如下：

导电率：广义欧姆定律

电流密度 $J$ 和电场 $E$ 之间的关系由广义欧姆定律表示：

其中，导电率$\sigma$描述材料响应电流的行为。与 $\epsilon$ 和 $\mu$ 一样，$\sigma$ 通常由二阶张量定义，并在各向同性导电材料中简化为标量。

多孔材料的导电率

在 Simcenter STAR-CCM+ 中，可以使用多孔区域（原有方法）或含多孔介质模型的流体区域（推荐方法）对多孔材料进行建模。

对于使用多孔介质模型的流体区域，分别定义流体和固体相的导电率：

对于多孔区域，可以使用各种方法将区域导电率建模为流体和固体组分的导电率组合：

$$\begin{array}{ll}\sigma =\frac{\chi }{\tau }{\sigma }_{\mathrm{fluid}}+\left(\frac{1-\chi }{\tau }\right){\sigma }_{\mathrm{solid}}& \mathrm{Volume\; Fraction\; Weighted\; Method}\\ \sigma ={\sigma }_{\mathrm{solid}}{(1-\chi )}^{\beta }& \mathrm{Bruggeman\; (solid)\; Method}\\ \sigma ={\sigma }_{\mathrm{fluid}}{\chi }^{\beta }& \mathrm{Bruggeman\; (fluid)\; Method}\end{array}$$

(4230)

其中， $\chi$ 为材料的孔隙率， $\tau$ 为曲率， ${\sigma }_{\mathrm{fluid}}$ 为标量， ${\sigma }_{\mathrm{solid}}$ 为二阶张量， $\beta$ 为 Bruggeman 近似指数。

使用 Bruggeman 方法计算有效导电率时，Simcenter STAR-CCM+ 会自动将多孔材料的曲率设为：

$$\begin{array}{c}\tau ={\chi }^{1-\beta }\end{array}$$

(4231)