载荷步进
对于具有非线性几何(大变形)和非线性材料(塑性或超弹性固体)的情况,控制方程可以为高度非线性,以使求解发散。要降低系统的非线性并改善收敛,便捷的方法是逐渐对多个步应用外部载荷。
考虑静态非线性问题:
(4627 4628 4631)
利用载荷步进,可以将 Eqn. (4627) 写为:
(4627 4628 4631)
其中,步进因子 考虑了载荷跨各步 的跃升。当前,Simcenter STAR-CCM+ 使用载荷循环方法。使用此方法将外部载荷拆分为逐步应用于各载荷步的多个部分。在每个载荷步中,使用牛顿-拉夫森法求解非线性系统 Eqn. (4627):
(4629 4630)
(4629 4630)
(4627 4628 4631)
线性载荷步进
线性载荷步控制根据先前各载荷步的收敛在每个步长应用载荷增量。如果当前载荷步为:
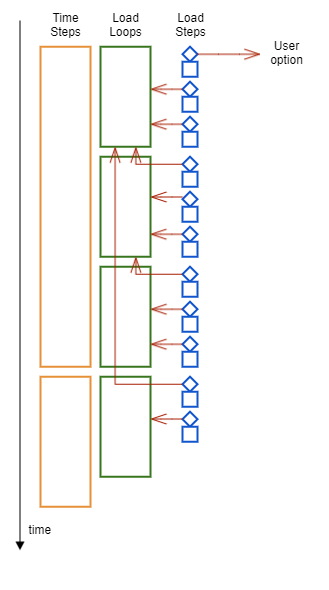
在每个载荷步中,求解器使用最小二乘法线性递增载荷:
- 模拟的第一个载荷步,则使用用户自定义初始载荷增量。
- 时间步的第一个载荷步,则考虑上一时间步的第一个载荷循环的所有载荷步。
- 载荷循环的第一个载荷步,则考虑上一载荷循环的所有载荷步。
- 载荷循环的后续载荷步,则考虑当前载荷循环的所有载荷步。

在每个载荷步中,求解器使用最小二乘法线性递增载荷:
(4632)
(4633)
其中,
是牛顿步的理想步数,
是下一载荷步的载荷步长,
是上一载荷步
的迭代次数,
是上一载荷步
的载荷步长。