逆模方法

可以从拉伸的所需横截面开始，然后计算回到生成它所需的模的形状。

在直接拉伸问题中，模表面全部固定，但自由流表面必须移动，这样才能满足动力和运动边界条件。 尤其是，自由流上的运动边界条件可以写为：

其中，$\mathbf{v}$ 为速度矢量场，$\mathbf{n}$ 为边界上的单位法向。 上述方程仅需要沿穿过每个速度流线的直线的一个边界条件。 对于直接拉伸，将对模唇施加此条件。 或者，可以在拉伸截面的末端（出口）采用边界条件，因此在这种情况下必须修改拉伸入口（模唇）。 这可以通过使模变形来实现。

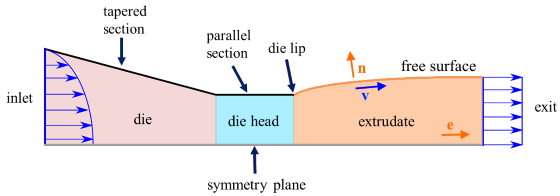
如上图所示，模修改通常由两个零部件组成：线性截面和短平行截面。 这两个截面都是拉伸方向 $\mathbf{e}$ 上线性修改的特殊情况。

基元微分几何的局部原理表示拉伸方向 $\mathbf{e}$ 的线性：

其中，$\mathbf{d}$ 为位移矢量。 上述方程的变分形式乘以加权函数 $\tilde{\mathbf{d}}$，然后在分部积分。 然后引入刚度系数 $k$ 以给出：

其中，$H_0^1\left(\mathrm{\Omega }\right)$ 表示由平方可积函数组成的 Sobolev 空间，其一阶导数也是平方可积，在具有重要（狄利克雷）边界条件的边界处的幅值为零。 但是，仅在法向（指向模边界）应用上述线性要求会得出：

锥化截面和平行截面之间的区别在于刚度 $k$ 的区别（平行截面的值大于锥化截面的值）。

最后，注意，逆模设计只能在稳态条件下使用。