合成涡法 (SEM)

合成涡法 (SEM) 是生成 LES 和 DES 所需的瞬时速度场的一种简单且有效的方法。

合成涡法由 Jarrin 等人 [368] 提出，它保留了涡方法 [366] 的概念基础，但更灵活且几乎不依赖于网格。

在 SEM 架构中，湍流流场被视为旋转涡的叠加，其旋转（顺时针或逆时针）和位置将根据标准化均匀分布绘制。 涡的大小是湍流的特征尺度。 由于涡必须跨至少两个网格单元才能产生相关信号，因此最小网格间距将对此湍流尺度施加限制。

用户分配的雷诺应力张量提供了该方法所需的相关函数。 如果此应力张量未知，则相关函数仅使用直接衍生自给定湍流强度的法向分量（各向同性假设）。

流入时生成的合成涡将在计算域中以平均流入速度进行对流和再循环。

SEM 生成的湍流结构只是真实湍流的近似值，必须允许其发展正确的相关性。 随着涡在下游对流，相关性自然发展。 要让此行为发生，流入边界和相关区域之间需保留足够的距离，这一点十分重要。

在一个间隔上产生波动的速度信号

该信号使用以下形状：

间隔限制基于流入区段的几何限制，如下图所示， ${\sigma }_i$ 是坐标方向 $i$ 的平均涡流长度尺度。

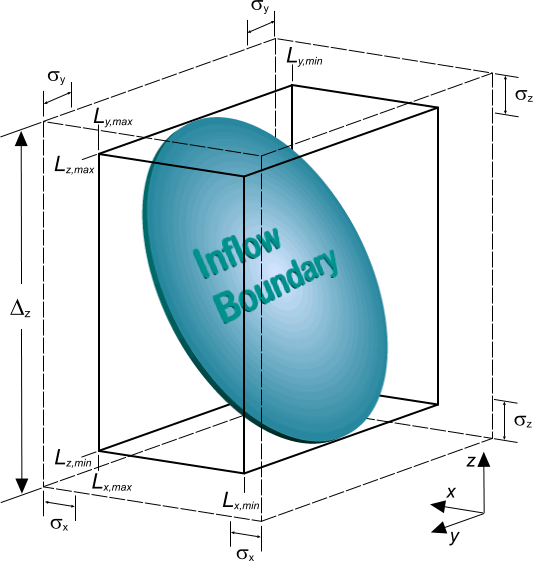
涡流的形状函数 $\mathbf{\text{f}}\left(\mathbf{\text{x}}\right)$ 满足以下归一化属性：

其中：

和 $i$ 为三个坐标方向的其中一个。 满足 Eqn. (1459) 的任何函数都可以作为形状函数。 在 Simcenter STAR-CCM+ 中，以下三角形函数用于表示第 k 次涡流在位置 ${\mathbf{\text{x}}}_k$ 对流入表面上的点 $\mathbf{\text{x}}$ 施加的影响：

其中：

• $x_i$ 为第 i 个方向的点 $\mathbf{\text{x}}$ 的坐标。
• $x_{i,k}$ 为第 i 个方向的涡流 k 的中心的坐标。

因此，每个涡流都有一个位置 ${\mathbf{\text{x}}}_k$ 、长度尺度 ${\mathbf{\text{σ}}}_k$ 和旋转方向，如下所示：

如 [367] 所示，旋转符号从均匀分布中随机选择，以确保所产生的速度信号满足：

上划线表示整体平均， ${\delta }_{ij}$ 是克罗内克增量。

涡湍流长度尺度 ${\mathbf{\text{σ}}}_k$ 原则上可以是空间的函数，并根据坐标方向而变化。 然而，在当前的执行中，假设湍流长度尺度是各向同性的：它可以根据空间中的位置而变化，它在任何一个点处在每个坐标方向必须具有相同的值。 其原因是初步研究表明，为了增加湍流长度尺度的各向异性值，与形状函数的分析归一化性质的偏离越来越大。 这将导致瞬时速度信号的失真，无法恢复规定的力矩。 此区域是当前正在研究的主题。

漩涡中心的坐标以体积 ${\Delta }_x\times {\Delta }_y\times {\Delta }_{\text{z}}$ 随机选择，其中 Eqn. (1460) 提供每个维度。 涡流数 N 通过该体积与平均涡流体积的比值得到，计算为 ${\overline{\sigma }}^3$，其中， $\overline{\sigma }$ 为平均涡流长度尺度。

调用冻结湍流的假设，每个涡流 k 的位置在每个坐标方向 i 上前进：

其中， $\Delta t$ 为时间间隔。

获得对流速度 V 作为平均流入速度分布的流入区域的平均值。 因此，波动速度信号获得为：

瞬时速度场计算如下：

因子 $a_{ij}$ 是从雷诺应力张量的 Cholesky 分解得到的：

其中：

当在入口处提供湍流强度时，调用各向同性假设，而不是应力张量的各个分量。 在这种情况下，根据强度和平均流入速度，依据以下关系计算雷诺应力张量的法向分量：

$\begin{array}{c}I=\sqrt{\frac{{\mathrm{v\prime \prime }}^2}{V^2}}\\ k=\frac{3}{2}{\mathrm{v\prime \prime }}^2\\ V^2=V_i{V}_i\end{array}$

得到结果：