6 自由度体的报告

Simcenter STAR-CCM+ 为 6 自由度体提供具体报告。 这些报告可用于可视化关键物理量，例如体在给定方向的加速度和速度、弹簧和悬链线耦合的长度，以及体方向。

沿指定方向的物理量分量

以下报告将计算沿指定方向的相应物理量分量：

• 6 自由度体加速度
• 6 自由度体角加速度
• 6 自由度体角动量
• 6 自由度体角速度
• 6 自由度体平移
• 6 自由度体速度
• 6 自由度体积力
• 6 自由度体积力矩

一般情况下，沿单位矢量 $\mathbf{d}$ 定义的方向的矢量 $q$ 的分量由以下公式给出：

$$q_{\mathbf{d}}=q\cdot \mathbf{d}$$

(4966)

例如，6 自由度体速度报告中对沿方向 $\mathbf{d}$ 的速度分量计算如下：

$$v_{\mathbf{d}}=\mathbf{v}\cdot \mathbf{d}$$

(4967)

其中，$\mathbf{v}$ 为体的总速度。 同样，6 自由度体积力报告对沿 $\mathbf{d}$ 的合力分量计算如下：

$$f_{\mathbf{d}}=f\cdot d$$

(4968)

其中，$f$ 为作用于体上的合力（请参见 Eqn. (4879)）。

6 自由度体方向

相对于初始体方向，计算绕指定轴的旋转角度。

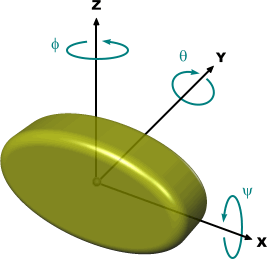
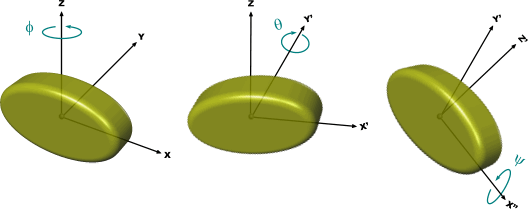
体方向遵循的欧拉角度约定，解释如下。 以 X-Y-Z 轴旋转为例。 对于此约定，三个旋转用于描述体的方向。 第一个旋转围绕基准坐标系的 X 轴（给出第一个欧拉角度）。 第二个旋转围绕基准坐标系的 Y 轴（给出第二个欧拉角度）。 第三个旋转围绕基准坐标系的 Z 轴（给出第三个欧拉角度）。 欧拉角度相对于固定旋转轴给出。

还可以相对于由之前旋转产生的移动旋转轴解释上述欧拉角度。 为此，从后向前读取各轴。 例如，X-Y-Z 轴旋转意味着第一个旋转围绕基准坐标系的 Z 轴。 第二个旋转围绕新坐标系的 Y 轴，该坐标系通过围绕 Z 轴旋转基准坐标系而创建。 第三个旋转围绕另一新坐标系的 X 轴，该坐标系通过围绕 Y 轴旋转上一坐标系而创建。

当第二个欧拉角度达到 $\frac{\pi }{2}$ 或 $-\frac{\pi }{2}$ 时，会发生万向节锁。 在万向节锁中，将仅确定第一个和第三个欧拉角度之和。 即使在万向节锁中，报告的欧拉角度也可正确描述体的方向。 但是，欧拉角度随时间变化的绘图可能出现不连续性。 因此，应尝试避免万向节锁，为此，选择欧拉角度约定时，应使第一个或第三个欧拉角度达到幅值 $\frac{\pi }{2}$。

6 自由度体旋转能量

体的旋转能量计算如下：

$$K_{rot}=\frac{1}{2}I\omega \cdot \omega$$

(4969)

其中，$I$ 为体的惯性矩张量，且 $\omega$ 为角速度。

6 自由度体弹簧伸长

计算 6 自由度体与环境之间或两个 6 自由度体之间的线性弹簧伸长，如线性弹簧耦合中所定义（请参见线性弹簧耦合）。 总长度为：

$$r=|{\mathbf{x}}_2-{\mathbf{x}}_1|$$

(4970)

其中，${\mathbf{x}}_1$ 和 ${\mathbf{x}}_2$ 为连接弹簧的端点。 相对于松弛长度 $l_{eq}$ 的伸长为：

$$r=|{\mathbf{x}}_2-{\mathbf{x}}_1|-l_{eq}$$

(4971)

6 自由度体总距离

计算两点之间的总距离：

$$r=|{\mathbf{x}}_2-{\mathbf{x}}_1|$$

(4972)

其中，${\mathbf{x}}_1$ 和 ${\mathbf{x}}_2$ 为两个点的位置矢量。

6 自由度悬链线长度

计算 6 自由度体与环境之间或两个 6 自由度体之间保持的悬链线长度，如悬链线耦合中所定义（请参见悬链线耦合）。 总长度为：

$$L=\underset{{\mathbf{x}}_1}{\overset{{\mathbf{x}}_2}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx$$

(4973)

其中，$y$ 为悬链线曲线（请参见 Eqn. (4952)），${\mathbf{x}}_1$ 和 ${\mathbf{x}}_2$ 为连接悬链线的端点。 相对于松弛长度 $l_{eq}$ 的悬链线长度为：

$$r=L-l_{eq}$$

(4974)

6 自由度分量距离

计算两个点之间沿指定方向的距离：

$$r=({\mathbf{x}}_2-{\mathbf{x}}_1)\cdot d$$

(4975)

其中，${\mathbf{x}}_1$ 和 ${\mathbf{x}}_2$ 为两个点的位置矢量，$d$ 为方向矢量。