体连接

可以将刚体与另一个刚体或环境相连接。Simcenter STAR-CCM+ 提供了几种方法来对连接进行建模，包括弹力和接触力。

弹簧-阻尼耦合

弹簧-阻尼耦合使用弹力和阻尼力连接两个体或一个体与其环境，其中，弹性部分由胡克定律给出。端点上的总力如下：

图 1. EQUATION_DISPLAY

\begin{array}{l} f_{1} (x) = k_{e f f} (x - x_{0}) + k_{d} \dot{x} \\ f_{2} (x) = - f_{1} (x) \end{array}

(4944)

在这里， $f_{1}$ 为作用于第一个端点位置矢量 $x_{1}$ 的力。 $f_{2}$ 为作用于第二个端点位置矢量 $x_{2}$ 的反作用力。 $x$ 为两个端点之间的距离（标量）。 $x_{0}$ 为弹力消失的距离（弹簧的松弛长度）。 $k_{e f f}$ 为有效弹性系数， $k_{d}$ 为阻尼系数。距离变化率 $\dot{x}$ 为两个端点的相对速度。两端点相背运动时，为正；相向运动时，则为负。

力的方向由从第一个端点到第二个端点的标准化方向矢量 $d$ 给出：

图 2. EQUATION_DISPLAY

\begin{array}{l} d = (x_{2} - x_{1}) / | x_{2} - x_{1} | \\ f_{1} = f_{1} \cdot d \\ f_{2} = f_{2} \cdot d \end{array}

(4945)

在上述方程中， $x_{1}$ 为弹簧的第一个端点附着的位置，而 $x_{2}$ 为弹簧的另一端。

弹力 $f_{e}$ 使用有效弹性系数 $k_{e f f}$ 进行定义：

图 3. EQUATION_DISPLAY

f_{e} (x) = k_{e f f} (x) \cdot (x - x_{0})

(4946)

在这里， $f_{e}$ 为第一个端点的弹力。

最简单的情况是线性弹力定律 - $f_{e} (x) = k \cdot (x - x_{0})$ ，有效弹性系数 $k$ 为常数。

对于非线性弹力定律的一般情况，可以根据已知 $f_{e} (x)$ 计算有效系数：

图 4. EQUATION_DISPLAY

k_{e f f} (x) = \frac{f_{e} (x)}{x - x_{0}}, x \neq x_{0}

(4947)

当 $x = x_{0}$ 时，可以使用 $k_{e f f} (x_{0}) = k (x_{0})$ ，其中， $k (x) = \frac{ⅆ f_{e} (x)}{ⅆ x}$ 为弹簧的非线性刚度。

如果已知弹簧刚度 $k (x)$ ，则可使用以下方程计算 $k_{e f f}$ ：

图 5. EQUATION_DISPLAY

k_{e f f} (x) = \frac{\int_{x_{0}}^{x} k (x´) ⅆ x´}{x - x_{0}}, x \neq x_{0}

(4948)

与上述方程类似，当 $x = x_{0}$ 时，可以使用 $k_{e f f} (x_{0}) = k (x_{0})$ 。

在某些应用中，松弛长度 $x_{0}$ 超出弹簧的操作范围，甚至可能未知。在此类情况下，可以选择弹簧操作范围之外的任意值 $x_{0}$ ，有效系数计算如下：

图 6. EQUATION_DISPLAY

k_{e f f} (x) = \frac{{f_{r} + \int}_{x_{r}}^{x} k (x´) ⅆ x´}{x - x_{0}}, x \neq x_{0}

(4949)

在这里， $f_{r}$ 为位于参考距离 $x_{r}$ 处的第一个端点的某一参考力。从 $x_{r}$ 到 $x$ 的距离必须位于弹簧的操作范围内，而 $x_{0}$ 位于范围之外的某个位置。

松弛长度为 $x_{0}$ 且有效弹性系数为 $k_{e f f} (x)$ 的非线性弹簧的示例如下：

图 7. EQUATION_DISPLAY

k_{e f f} (x) = a + b (x - x_{0}) + c {(x - x_{0})}^{2}

(4950)

在这里， $a$ 、 $b$ 和 $c$ 为常数值。弹簧的第一个端点上的弹力如下：

图 8. EQUATION_DISPLAY

f (x) = k_{e f f} (x) \cdot (x - x_{0}) = a (x - x_{0}) + b {(x - x_{0})}^{2} + c {(x - x_{0})}^{3}

(4951)

$k_{e f f} (x)$ 和 $f (x)$ 的项是 $(x - x_{0})$ 中的多项式。

悬链线耦合

悬链线耦合对弹性的准固定悬链线（如链或牵引绳）进行建模，悬链线悬挂在两个端点之间，承受重力场导致的自身重量。在局部笛卡尔坐标系中，悬链线的形状由以下参数方程组给定：

图 9. EQUATION_DISPLAY

\begin{matrix} x = a u + b \sinh (u) + α \\ y = a \cosh (u) + \frac{b}{2} \sinh^{2} (u) + β \\ for u_{1} \leq u \leq u_{2} \end{matrix}

(4952)

其中：

$a = \frac{c}{λ_{0} g}$

$b = \frac{c a}{D L_{e q}}$

$c = \frac{λ_{0} L_{e q} g}{\sinh (u_{2}) - \sinh (u_{1})}$

在这些方程中， $g$ 为重力加速度， $λ_{0}$ 和 $L_{e q}$ 分别是无力条件下悬链线的单位长度质量和松弛长度。 $D$ 为悬链线刚度， $α$ 和 $β$ 为积分常数，取决于两个端点的位置和悬链线的总质量。曲线参数 $u$ 与悬链线曲线倾角 $ϕ$ 的关系如以下方程所示：

图 10. EQUATION_DISPLAY

\tan ϕ = \sinh (u)

(4953)

参数值 $u_{1}$ 和 $u_{2}$ 表示悬链线端点 $p_{1}$ 和 $p_{2}$ 在参数空间中的位置。

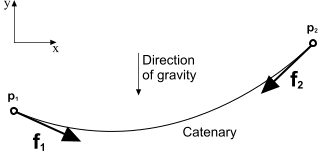
作用于悬链线两个端点的力 $f_{1}$ 和 $f_{2}$ 分别沿着参数值 $u_{1}$ 和 $u_{2}$ 处的悬链线曲线的局部切线矢量方向。它们由以下表达式给定：

图 11. EQUATION_DISPLAY

\begin{array}{l} f_{1, x} = c \\ f_{1, y} = c \sinh (u_{1}) \end{array}

(4954)

且

图 12. EQUATION_DISPLAY

\begin{array}{l} f_{2, x} = - c \\ f_{2, y} = - c \sinh (u_{2}) \end{array}

(4955)

这些力和生成的悬链线曲线如下图所示。

接触耦合

对于连续体，接触耦合可防止与刚体关联的边界与另一个边界接触，另一个边界可以是计算域的边界（体-环境耦合）或与另一个连续体关联的边界（体-体耦合）。

为了防止接触，模型应用了取决于刚体边界与相对边界之间的距离的接触力。当体边界与另一个边界之间的距离大于用户指定的有效范围时，接触力下降到零。如果距离小于有效范围，则应用排斥接触力。

边界面 $f$ 上的接触力可以写为：

图 13. EQUATION_DISPLAY

f_{f} = f_{n} + f_{t}

(4956)

其中， $f_{n}$ 为法向分量，它可防止接触； $f_{t}$ 为切向分量，它对沿相对边界的体的摩擦建模。

接触力将围绕当前的体位置 $r_{b}$ 创建力矩 $m_{f}$ ：

图 14. EQUATION_DISPLAY

m_{f} = (r_{f} - r_{b}) \times f_{f}

(4957)

其中， $r_{f}$ 是面 $f$ 的面形心位置。体上的总力和总力矩都是体表面的所有面的所有贡献的总和。

接触力的法向分量可以写为：

图 15. EQUATION_DISPLAY

f_{n} (d_{f}) = a_{f} [k_{1} (d_{0} - d_{f}) - k_{2} {\dot{d}}_{f}] n_{b f}

(4958)

其中， $k_{1}$ 为弹性系数， $k_{2}$ 为阻尼系数， $a_{f}$ 为面网格面积， $d_{f}$ 为面形心和相对边界之间的距离， $d_{0}$ 为有效范围， $n_{b f}$ 为面 $f$ 旁的边界面的法向。

弹性系数

k_{1}

对在接触之前停止刚体至关重要。要计算冲击情况下此系数的值，可应用以下关系：

体-体耦合：
图 16. EQUATION_DISPLAY

$k_{1} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \cdot \frac{1}{A} \cdot \frac{v_{n, r e l}^{2}}{{(d_{0} - d_{m i n})}^{2}}$
(4959)
体-环境耦合：

图 17. EQUATION_DISPLAY

k_{1} = \frac{m_{1}}{A} \cdot \frac{v_{n, r e l}^{2}}{{(d_{0} - d_{m i n})}^{2}}

(4960)

其中， $m_{1}, m_{2}$ 指示体 1 和 2 的质量， $A$ 为估计的接触面积， $v_{n, r e l}$ 为两个耦合对象的法向相对冲击速度， $d_{m i n}$ 为最小距离。体应该在达到此距离前停止。

通过应用接触力停止体所需的时间计算如下：

体-体耦合：
图 18. EQUATION_DISPLAY

$τ = \frac{π}{2} \sqrt{\frac{m_{1} \cdot m_{2}}{(m_{1} + m_{2}) A k_{1}}}$
(4961)
体-环境耦合：
图 19. EQUATION_DISPLAY

$τ = \frac{π}{2} \sqrt{\frac{m_{1}}{A k_{1}}}$

(4962)

要解决停止过程，模拟时间步必须足够小于 $τ$ 。或者，6 自由度求解器可以使用子步。上述关系仅适用于弱阻尼。

要计算阻尼系数的值，可应用以下关系：

体-体耦合：
图 20. EQUATION_DISPLAY

$k_{2} = 2 ς \sqrt{\frac{{(m}_{1} \cdot m_{2}) k_{1}}{(m_{1} + m_{2}) A}}$

(4963)
体-环境耦合：
图 21. EQUATION_DISPLAY

$k_{2} = 2 ς \sqrt{\frac{m_{1} k_{1}}{A}}$
(4964)

其中， $ς$ 为描述阻尼量的常数因子。一般情况下， $ς$ 应足够小 ( $ς ≪ 1$ )，因为大 $ς$ 值与大时间步组合会导致数值不稳定。

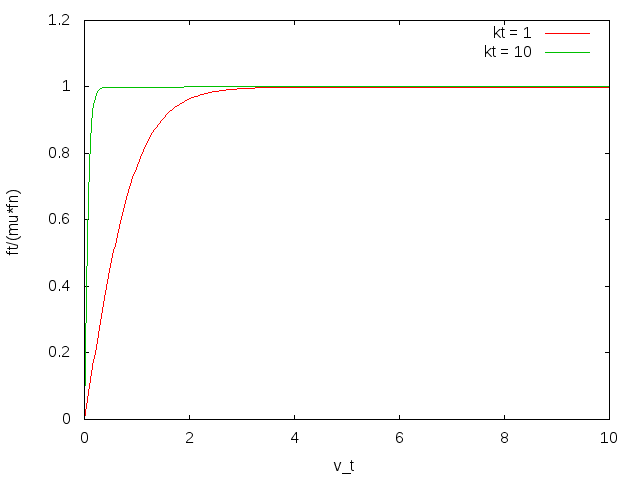
面 $f$ 上的接触力的切向分量由以下公式给出：

图 22. EQUATION_DISPLAY

f_{t} = - μ | f_{n} | \tanh (k_{t} v_{t})

(4965)

其中， $μ$ 为摩擦系数， $k_{t}$ 为 Tanh 系数， $v_{t}$ 为相对于相对边界的面 $f$ 的切向速度。

此切向力分量可以对体和边界之间的动摩擦进行建模。不考虑静摩擦。Tanh 函数可在相对滑动速度较小时稳定摩擦力。

当滑动速度 $v_{t} ≫ 1 / k_{t}$ 时，摩擦力仅取决于摩擦系数、法向力和相对速度的方向。滑动速度增大时，摩擦力保持不变，具体取决于 $k_{t}$ 。对于较小的滑动速度，摩擦力还取决于速度幅值。