H¹ 拉格朗日形状函数

固体力学应用使用等参单元，其中单元拓扑和主要未知量使用相同的近似阶（即，它们使用相同多项式阶次的形状函数进行插值）。

Simcenter STAR-CCM+ 提供 2D 线性、3D 线性和 3D 二次拉格朗日单元 [947]。 未知量存储在单元节点处。 通过在每条边的角节点之间添加中间边节点，可提高二次单元的精度。

2D 线性单元
三角形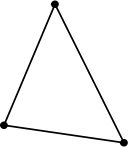	四边形

3D 线性单元
Tet4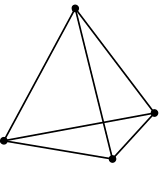	Wedge6	Hex8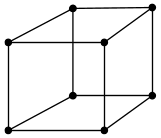	Pyramid5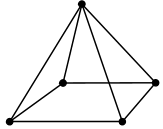

3D 二次单元
Tet10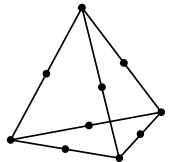	Wedge15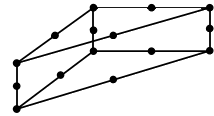	Hex20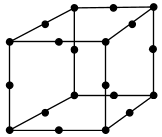	Pyramid13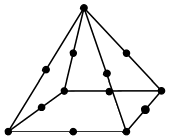

考虑具有 $n$ 个节点的单元。 定义局部坐标系非常方便，以便可以使用局部坐标 $\xi$ 定义单元中任意点的位置。

如果 ${\xi }_P$ 是局部坐标系中点 $P$ 的位置矢量，则点 $P$ 处的 $u$ 值可以写为：

如果 $M$ 和 $N$ 为两个单元节点，且 $M\ne N$，则定义 ${\mathcal{N}}_M$ 以使：

线性四面体 (Tet4)

在四面体单元中，局部坐标为 $0\le \begin{array}{c}{\xi }_i\hfill \end{array}\le 1$：

坐标点 $({\begin{array}{c}\xi \end{array}}_1,{\begin{array}{c}\xi \end{array}}_2,{\begin{array}{c}\xi \end{array}}_3)$ 处的节点形状函数只是以下值：

$$\begin{array}{ccc}{\mathcal{N}}_1& =& {\begin{array}{c}\xi \end{array}}_1\hfill \\ {\mathcal{N}}_2& =& {\begin{array}{c}\xi \end{array}}_2\hfill \\ {\mathcal{N}}_3& =& {\begin{array}{c}\xi \end{array}}_3\hfill \\ {\mathcal{N}}_4& =& {1-\begin{array}{c}\xi \end{array}}_1{-\begin{array}{c}\xi \end{array}}_2{-\begin{array}{c}\xi \end{array}}_3\hfill \end{array}$$

(4806)

它们对应于重心坐标。

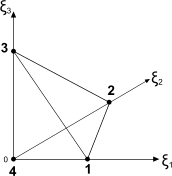
线性六面体 (Hex8)

在六面体单元中，局部坐标为 $-1\le \begin{array}{c}{\xi }_i\hfill \end{array}\le 1$：

坐标点 $({\begin{array}{c}\xi \end{array}}_1,{\begin{array}{c}\xi \end{array}}_2,{\begin{array}{c}\xi \end{array}}_3)$ 处的节点形状函数为以下值：

$${\mathcal{N}}_M({\xi }_i)=\frac{1}{8}(1+{\xi }_{iM}{\xi }_i);M=1,\mathrm{...},8$$

(4807)

线性六面体具有丰富的气泡自由度以克服锁定现象。 例如，线性形状函数 Eqn. (4807) 不提供足够的模态形状来近似固体力学应用中的剪切和弯曲，导致单元过于刚硬。 对于长宽比高且偏斜的单元形状，刚化效应更为严重。 为了克服锁定，Simcenter STAR-CCM+ 将三个额外矢量 $u_{oi}$（即 9 个内部或气泡自由度）添加到节点物理量 $u_M$：

$$\begin{array}{cc}u({\xi }_i)={\displaystyle {\mathcal{N}}_M}({\xi }_i)u_M+{\displaystyle u_{oi}}(1-{\xi }_i^2);& i=1,2,3;M=1,\mathrm{...},8;\end{array}$$

(4808)

二次 Hex20 单元的精度高于具有气泡函数的线性 Hex8 单元的精度。 Hex20 也对高长宽比和偏斜情况不敏感。 Tet4 单元在弯曲和剪切中表现为刚性，使用气泡函数无法改进其行为。

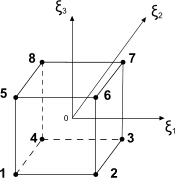
从局部到全局：参数化映射

父域和全局物理域之间的局部到全局映射可确保相邻单元之间的连续性。

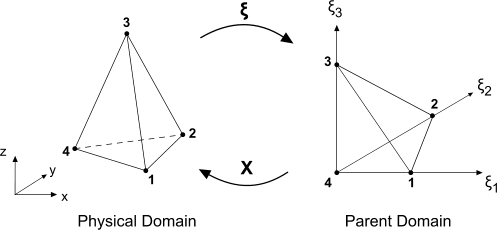
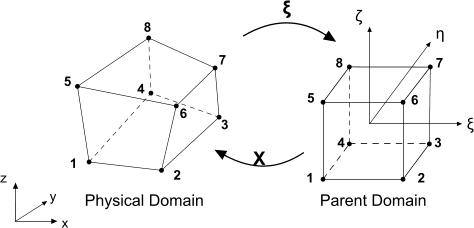
形状函数导数

变量 $u$ 对未变形坐标 $X$ 的导数通过以下公式与节点物理量 $u_M$ 相关：

形状函数对未变形物理坐标的导数通过以下公式由形状函数对自然坐标的导数得出：

其中：

$J^{-1}$ 为雅可比变换 $J$ 的逆变换：