有限元网格质量度量

有限元分析中网格的质量度量包括偏斜角、长宽比、中点偏差、形状和翘曲。这些网格单元质量度量可用于识别可能产生不准确结果或缓慢收敛的质量较差的网格单元。选择有限元模型后，可以在带有或不带中间节点的六面体、四面体、楔形体和棱锥体单元类型上以及在四边形和三角形等 2D 单元上计算关联的场函数。

这些质量度量不是在任意网格单元上定义的。任意 3D 网格单元并不总是适用于有限元计算 - 质量度量无法计算，因此，在这种情况下，默认值设为 –∞。

所有物理量都表示有限元网格单元与理想单元的偏差。理想单元定义为具有单位边长的指定类型的单元。

每个度量都有一个用于计算网格单元质量 $q$ 的特定公式。

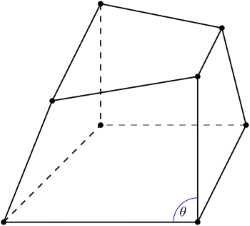
偏斜角

偏斜角是等角度偏斜的度量，定义如下：

$$q=1-\max (\frac{\theta -{\theta }_c}{180-{\theta }_c},\frac{{\theta }_c-\theta }{{\theta }_c})$$

(4840)

其中， $\theta$ 为单元中的面顶点的角度， ${\theta }_c$ 是理想单元的面中对应顶点的角度（三角形面为 60°，四边形面为 90°）。 $q$ 的最小值被接收到单元的所有拐角顶点。

$q$ 位于间隔 [0, 1] 中，其中 0 为不良网格单元，1 为理想网格单元。此指标无法识别六边形面单元。

长宽比

质量 $q$ 被计算为最大边长 $h_{\text{max}}$ 与最小边长 $h_{\text{min}}$ 的比值：

$$q=\frac{h_{\text{max}}}{h_{\text{min}}}$$

(4841)

$q$ 位于间隔 [1,∞] 中，其中 $q=1$ 为最佳质量， $q\gg 1$ 为较差质量。对于良好单元， $q<10$ 。

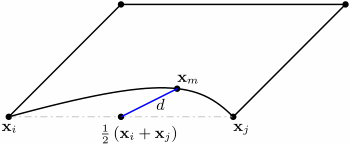
中点偏差

此度量适用于具有中间边顶点的单元。通过查看中间边顶点的放置以及对拐角顶点之间直线的偏离，检查每条单元边（拐角顶点 ${\mathbf{x}}_i$ 和 ${\mathbf{x}}_j$ 、中间边顶点 ${\mathbf{x}}_m$ ）。

$$q=\text{max}\left[\frac{d}{l_e}\right]=\text{max}\left[\frac{\Vert {\mathbf{x}}_m-\frac{1}{2}({\mathbf{x}}_i+{\mathbf{x}}_j)\Vert }{l_e}\right]$$

(4842)

其中

• $d$ 是从 ${\mathbf{x}}_i$ 和 ${\mathbf{x}}_j$ 之间的中点（即 $\frac{1}{2}({\mathbf{x}}_i+{\mathbf{x}}_j)$ ）到 ${\mathbf{x}}_m$ 的距离。
• $l_e$ 为平均边长。

$q$ 位于间隔 [0,∞] 中，其中 $q=0$ 为理想单元。对于良好单元， $q<0.25$ 。

形状

此度量基于变换矩阵 $\mathbf{T}$ 的雅可比行列式（雅可比），它将坐标从理想单元转换为物理单元。在所有单元顶点上计算雅可比，包括中间边顶点。形状函数质量 $q$ 将作为所有单元顶点处的最小值，计算如下：

$$q=D\frac{\text{det}{\left(\mathbf{T}\right)}^{\frac{2}{D}}}{{\left|\mathbf{T}\right|}^2}$$

(4843)

其中：

• $q$ 位于间隔 [0,1] $\cup$ {–1} 中，其中 $q=1$ 为理想单元。对于具有负雅可比的单元， $q=-1$ 。
• $D$ = 3 用于三维情况，= 2 用于二维情况。
• $\left|\mathbf{T}\right|$ 为 Frobenius 矩阵范数。

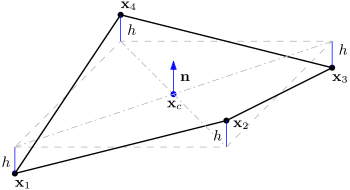
翘曲

此度量是面顶点与面平面的最大距离 $h$ 除以平均边长 $l_e$ 。

$$q=\frac{\text{max}h}{l_e}=\text{max}\frac{\mathbf{n}\cdot ({\mathbf{x}}_j-{\mathbf{x}}_c)}{l_e}$$

(4844)

其中：

• $\mathbf{n}$ 为法向矢量。
• ${\mathbf{x}}_j$ 为面顶点。
• ${\mathbf{x}}_c$ 为面平面上的任何点。

对于体积单元，它是面平面上所有面的最大归一化距离。对于带拐角顶点 ${\mathbf{x}}_1$ 、 ${\mathbf{x}}_2$ 和 ${\mathbf{x}}_3$ （面中心为 ${\mathbf{x}}_c$ ）的三角形面，法向矢量的计算如下：

$$\mathbf{n}=\frac{({\mathbf{x}}_2-{\mathbf{x}}_1)\times ({\mathbf{x}}_3-{\mathbf{x}}_1)}{\Vert ({\mathbf{x}}_2-{\mathbf{x}}_1)\times ({\mathbf{x}}_3-{\mathbf{x}}_1)\Vert }\text{, }{\mathbf{x}}_c=\frac{{\mathbf{x}}_1+{\mathbf{x}}_2+{\mathbf{x}}_3}{3}$$

对于带拐角顶点 ${\mathbf{x}}_1$ 、 ${\mathbf{x}}_2$ 、 ${\mathbf{x}}_3$ 和 ${\mathbf{x}}_4$ 的四边形面，法向矢量计算为对角线的法向量 $\mathbf{n}={\mathbf{t}}_1\times {\mathbf{t}}_2$ ，其中：

$$\begin{array}{l}{{\mathbf{d}}_1={\mathbf{x}}_3-{\mathbf{x}}_1,\mathbf{d}}_2={\mathbf{x}}_2-{\mathbf{x}}_4\\ \begin{array}{c}{\mathbf{t}}_1=\frac{{\mathbf{d}}_1+{\mathbf{d}}_2}{\Vert {\mathbf{d}}_1+{\mathbf{d}}_2\Vert },{\mathbf{t}}_2=\frac{{\mathbf{d}}_1-{\mathbf{d}}_2}{\Vert {\mathbf{d}}_1-{\mathbf{d}}_2\Vert }\end{array}\end{array}$$

且

$${\mathbf{x}}_c=\frac{{\mathbf{x}}_1+{\mathbf{x}}_2+{\mathbf{x}}_3+{\mathbf{x}}_4}{4}$$

$q$ 位于间隔 [0,∞] 中，其中 $q=0$ 为理想单元。对于良好单元， $q\le 0.5$ 。