H(Curl) Hierarchical Shape Functions

When formulating Maxwell's equations with the magnetic vector potential as dependent variable, the differential equations include second order curl-curl derivatives, so that their integral weak form includes first order curl derivatives. Furthermore, a tangential continuity condition is imposed on the vector potential and a high accuracy on the derived differential fields is desirable. These problems require shape functions whose tangential component is continuous over the space domain and their curl is well-defined. Typical interpolation functions that satisfy these requirements are the H(Curl)-conforming hierarchical shape functions.

The form of the shape functions depends on the element topology and order. Simcenter STAR-CCM+ offers 2D and 3D lowest order Nédélec elements of the first kind [946].


2D Elements
Triangle	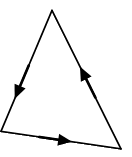Quad


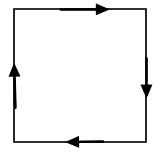3D Elements
Tetrahedron	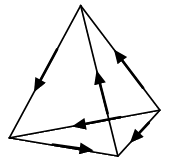Wedge	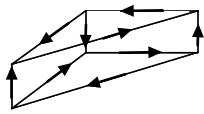Hexahedron	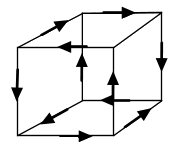Pyramid

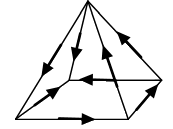Consider an element with n edges. The distribution of a variable $u$ can be approximated by:

图 1. EQUATION_DISPLAY

\begin{matrix} u = N_{M} u_{M} \end{matrix}

(4813)

where:

the index $M = 1, ..., n$ identifies the element degrees of freedom
$u_{M}$ is the $M$ -th scalar degree of freedom
$N_{M}$ is a vector H(Curl)-conforming shape function, which determines the contribution of the scalar value $u_{M}$ to $\begin{matrix} u \end{matrix}$

In particular, for lowest order Nédélec elements of the first kind:

the degrees of freedom are located at the element edges
the number of degrees of freedom coincides with the number of element edges
the degree of freedom can be identified as the first moment of the tangential component over each edge:
图 2. EQUATION_DISPLAY

$u_{M} = \int_{E_{M}} A \cdot τ d s$
(4814)

where $τ$ is the tangential vector along edge $E_{M}$
the shape functions have constant tangential trace on the edges of the element:
图 3. EQUATION_DISPLAY

$N_{M} \cdot τ_{E_{N}} = \frac{1}{| E_{N} |} δ_{M N}$
(4815)

which yields the nodality of the basis.

The shape functions for tetrahedral elements are described below.

Tetrahedron

In a tetrahedron, the edge shape function for the edge $E_{M}$ between the nodes $e_{1}$ and $e_{2}$ is defined as:

图 4. EQUATION_DISPLAY

${\hat{N}}_{M} = \nabla_{ξ} N_{e_{1}} N_{e_{2}} - N_{e_{1}} \nabla_{ξ} N_{e_{2}}$
(4816)

In particular, for the edge going between the nodes 1 and 4 in the reference element, the shape function takes the explicit form:

图 5. EQUATION_DISPLAY

${\hat{N}}_{[1; 4]} = [\begin{matrix} - 1 + ξ_{2} + ξ_{2} \\ - ξ_{1} \\ - ξ_{1} \end{matrix}]$
(4817)

The shape function has a tangential component along edge $[1; 4]$ , but is perpendicular to all other edges.

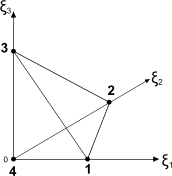
Higher-Order Shape Functions

When using a higher-order finite element method, further degrees of freedom (in addition to those used for the lowest-order scheme) are used to discretize the finite element space. The additional degrees of freedom are added in sequence to the edges, followed by the faces, and finally the cell interior.

The higher-order shape functions are formulated in a hierarchical manner, that is, the set of finite element shape functions for any element of order $p$ contains the set of shape functions for the element of order $p - 1$ .

In this way, the shape functions for any higher-order element are built from the shape functions of the element of sequentially lowest-order. The lowest-order shape functions remain precisely as those described above. The coefficients of the polynomial from which the H(Curl)-conforming finite element shape functions are constructed are typically computed via a recursion formula [reflink].

The H(curl) conformity of the elements are ensured by defining a local finite element space,

V_{p}

, on each element,

K

, with the property that tangential traces of an arbitrary function,

v

, on all element edges,

E

, and element faces,

F

, belong to polynomial space of a specific order

p

[reflink].

V_{p} (K) : = {v \in {(P^{P_{C}} (K))}^{3} | {t r}_{τ, F} (v) \in P^{p_{F}} \forall F \in ℱ_{K}, {t r}_{τ, E} (v) \in P^{p_{E}} \forall E \in ε_{K}}

(4818)

p

represents the set of polynomial degrees corresponding to the element edges, faces, and the cell itself and is defined as:

p = {p_{E_{1}}, ..., p_{E_{n (e d g e s)}}, p_{F_{1}}, ..., p_{F_{n (f a c e s)}}, p_{C}}

(4819)

The set of polynomial degrees have a minimum order rule enforced upon them such that the polynomial space,

V_{p} (K)

, is well defined and it holds that

\nabla W_{p + 1} (K) \subset V_{p} (K)

for the H(One)-conforming local finite element space

W_{p + 1} (K)

of the associated polynomial order.

p_{c} \geq p_{F} \geq p_{E}

(4820)

The tangential traces for functions onto edges and faces are respectively defined as [reflink]:

{t r}_{E, τ} (v) : = {t r}_{E} (v \cdot τ)

(4821)

{t r}_{F, τ} (v) : = {t r}_{F} (n \times (v \times n))

(4822)

where $n$ is the face normal.

Following this, the degrees of freedom that define a H(Curl)-conforming, uni-solvent finite element are [reflink]:

Degrees of freedom with generalized support points on edges: $\begin{matrix} N_{i}^{E} (u) = \int_{E} u \cdot τ v_{i} d S & f o r {v_{i}}_{0 \leq i \leq P_{E}} \end{matrix}$

(4823)
Degrees of freedom with generalized support points on faces: $\begin{matrix} N_{i}^{F} (u) = \int_{F} (\nabla_{F} \times u) \cdot (\nabla_{F} \times v_{i}) d A & f o r {v_{i}} s u c h t h a t {\nabla_{F} \times v_{i}} i s a b a s i s o f \nabla_{F} \times (P_{0, τ}^{p_{F}} (F)) \end{matrix}$

(4824)

$\begin{matrix} N_{i}^{F} (u) = \int_{F} u \cdot v_{i} d A & f o r {v_{i}} b e i n g a b a s i s o f \nabla_{F} (P_{0}^{p_{F} + 1} (F)) \end{matrix}$

(4825); where $\nabla_{F} \times v = (\nabla\times v) \cdot n$ and $(P_{0, τ}^{p_{F}} (F)) : = {(P^{p_{F}} (F))}^{2} \cap H_{0} (c u r l, F)$
Degrees of freedom with generalized support points in the cell interior: $\begin{matrix} N_{i}^{C} (u) = \int_{F} (\nabla_{F} \times u) \cdot (\nabla_{F} \times v_{i}) d V & f o r {v_{i}} s u c h t h a t {\nabla_{F} \times v_{i}} i s a b a s i s o f \nabla_{F} \times (P_{0, τ}^{p_{C}} (K)) \end{matrix}$

(4826); $\begin{matrix} N_{i}^{C} (u) = \int_{F} u \cdot v_{i} d A & f o r {v_{i}} b e i n g a b a s i s o f \nabla_{F} (P_{0}^{p_{C} + 1} (K)) \end{matrix}$

(4827); where

$(P_{0, τ}^{p_{C}} (K)) : = {(P^{p_{C}} (K))}^{3} \cap H_{0} (c u r l, K)$

(4828)

The resultant higher-order shape functions for the H(Curl) space are classed into several categories depending on their formulation. A subset of the shape functions (excluding the lowest-order shape functions) are referred to as the gradient shape functions, as they are expressed in terms of gradients of H(One) shape functions. In some circumstances, these shape functions can be omitted as they have no contribution during the assembly of the discrete problem due to the identity:

\nabla\times \nabla N_{i} = 0

(4829)

Local-to-Global Mapping

Local-to-global mapping between the element domain and the global physical domain ensures continuity across adjacent elements:

图 6. EQUATION_DISPLAY

N = j^{- T} \cdot \hat{N} (ξ (x))

(4830)

where

j = \partial x / \partial ξ

and

x

is the physical deformed coordinate.

Shape Function Derivatives

The curl of the shape functions with respect to the deformed coordinates is given by:

图 7. EQUATION_DISPLAY

\nabla_{x} \times N = j^{- 1} j \cdot \nabla_{ξ} \times \hat{N} (ξ (x))

(4831)

where $j = \det j$