使用延伸函数

延伸函数可确定用于生成网格单元层厚度分布的基础公式。

提供了两个选项：“几何级数”和“双曲正切”。

几何级数

此默认选项使用简单的几何关系来分布网格单元层。 相邻网格单元层之间的延伸因子将始终作为常数值进行计算。 下面显示了使用几何级数与 10 个层构建的棱柱层示例。 对整个棱柱层使用棱柱层延伸因子 1.5（默认值）。



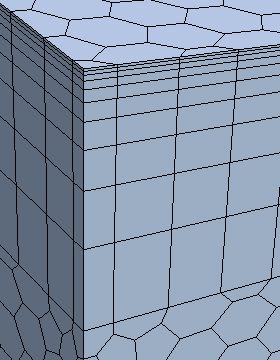
双曲正切

此选项可根据单参数双曲正切延伸函数分布网格单元层：

s(ni)⁢= 1⁢+ tanh⁡[Fs(ni/N−1)]tanh⁡(Fs)
(83)

其中，N 为总层数，ni 为当前节点，Fs 为总体延伸因子，s(ni) 为节点 ni 的分布值。 注意，由于 0≤ni≤N  ，因此如果层数为 5，则 ni 的值为 0、1、2、3、4 和 5。

有关详细信息，请参见棱柱层网格参考书目。

下图描绘了节点和层之间的关系。



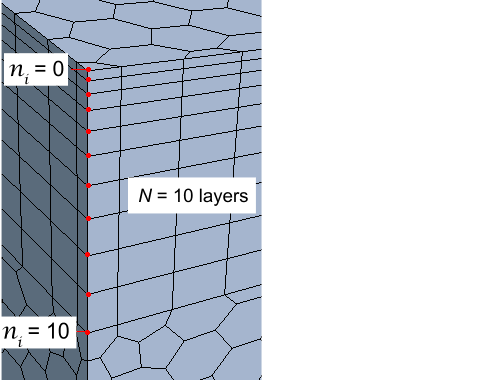
上图显示了层数为 10 且总体棱柱层延伸因子为 1.5 时的分布。 层之间的尺寸比率不再是常数，而是修改为使整个棱柱层的网格单元厚度之间的过渡更平滑。 此选项可用于减小近壁棱柱层的间距，同时避免外部棱柱层出现大间距。