火焰传递函数

非稳态热释放波动对声压的影响使用火焰响应模型进行建模。Simcenter STAR-CCM+ 提供 N-Tau 模型或用户 N-Tau 模型。这些模型使用时间延迟来考虑热释放振荡与压力振荡响应之间的有限时间。

燃烧室中热声学不稳定的通用机制如下所示。火焰处的热释放波动会创建声压波，该波向上游方向传播并调节燃料流率。这会导致当量比波动，该波动向下游方向对流至火焰区域，并导致热释放波动，并且此循环继续进行。因此，非稳态燃烧对声压的影响因入口到火焰的大致对流时间而延迟。其他不稳定机制也以时间延迟为特征。

Simcenter STAR-CCM+ 使用 N-Tau 模型对火焰传递函数（即非稳态热释放对声场的影响）进行建模，其中 N 为乘数（称为相互作用指数），Tau 是指定的时间延迟。

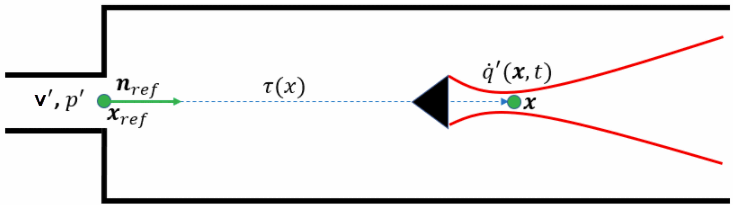
N-Tau 模型

简化的 N-Tau 模型通过以下方式计算燃烧热释放源：

图 1. EQUATION_DISPLAY

\hat{q} (x) = \frac{q_{t o t}}{i ω ρ_{0} (x_{r e f}) U_{b u l k}} n_{u} (x) e^{i ω τ (x)} \nabla \hat{p} (x_{r e f}) \cdot n_{r e f}

(4790)

其中，

q_{t o t}

为总热释放，

i

为虚部数字

\sqrt{- 1}

，

ω

为声频（特征值），

ρ_{0}

为混合物密度，

x_{r e f}

为通常位于燃烧器入口处的参考位置，

U_{b u l k}

为体积速度，

n_{u} (x)

为相互作用指数，

τ (x)

为时间滞后，

\hat{p}

为平均压力，

n_{r e f}

为参考单位矢量，表示从参考位置到火焰的方向（如上图所示）。

相互作用指数 $n_{u} (x)$ 对应于火焰响应的幅值 $n$ （位于 $x$ ）。

基于 Nicoud F. 等人的发现 [742]，假设

n_{u} (x)

在火焰区域内是恒定的 - 热释放率非零：

图 2. EQUATION_DISPLAY

n_{u} (x) = η = \frac{n}{δ_{f}} \frac{U_{b u l k}}{q_{t o t}} \frac{γ p_{0}}{γ - 1}

(4791)

热释放率为零的其他位置。

图 3. EQUATION_DISPLAY

n_{u} (x) = 0

(4792)

其中，

η

为火焰内热效率的常数值，

δ_{f}

为火焰厚度，

γ

为绝热热容比系数 (

\frac{C_{p}}{C_{v}}

)，

p_{0}

为参考压力，

n

为用户自定义标量常数。

在 Simcenter STAR-CCM+ 中，Eqn. (4791) 乘以按比例缩放的热释放率：

图 4. EQUATION_DISPLAY

n_{u} (x) = η = \frac{n}{δ_{f}} \frac{U_{b u l k}}{q_{t o t}} \frac{γ p_{0}}{γ - 1} {\dot{q}}_{s c a l e d} (x)

(4793)

其中：

图 5. EQUATION_DISPLAY

{\dot{q}}_{s c a l e d} (x) = (\frac{\dot{q} (x) - {\dot{q}}_{\min}}{{\dot{q}}_{\max} - {\dot{q}}_{\min}})

(4794)

Simcenter STAR-CCM+ 为简化的 N-Tau 模型（假设指定的恒定时间延迟）计算燃烧热释放源

τ (x) = τ

图 6. EQUATION_DISPLAY

\hat{q} (x) = \frac{n}{δ_{f}} {\dot{q}}_{s c a l e d} (x) \frac{γ p_{0}}{i ω ρ_{0} (x_{r e f}) (γ - 1)} e^{i ω τ} \nabla \hat{p} (x_{r e f}) \cdot n_{r e f}

(4795)

火焰厚度

δ_{f}

通过以下方式计算：

图 7. EQUATION_DISPLAY

δ_{f} = {[\int {\dot{q}}_{s c a l e d} d V]}^{1 / 3}

(4796)

Simcenter STAR-CCM+ 由上述表达式获得火焰响应矩阵如下：

图 8. EQUATION_DISPLAY

D (ω) \hat{P} = \int i ω (γ - 1) \hat{q} d V

(4797)

用户 N-Tau 模型

（广义化）用户 N-Tau 模型通过以下方式计算燃烧热释放源：

图 12. EQUATION_DISPLAY

\hat{q} (x) = \frac{q_{t o t}}{i ω ρ_{0} (x_{r e f}) U_{b u l k}} n_{u} (x) e^{i ω τ (x)} \nabla \hat{p} (x_{r e f}) \cdot n_{r e f}

(4801)

其中，

n_{u} (x)

为用户指定的全相互作用指数字段，

τ (x)

为用户指定的整个时间延迟字段。

$x_{r e f}$ 为参考位置， $n_{r e f}$ 为参考方向， $U_{b u l k}$ 为体积速度。