宽带噪声源模型
对于近场预测,Simcenter STAR-CCM+ 提供了一组能够评估宽带噪声源的模型。噪声源包含四极源的体积分布和偶极源的表面分布。
在频率域中,宽带噪声具有连续的频谱,其中,声能在给定范围内的所有频率处连续分布。这些模型可以计算空气动力生成的主要噪声源的位置和强度。它们使用雷诺平均纳维-斯托克斯 (RANS) 湍流方程的流场物理量。由于这些宽带噪声模型使用 RANS 模拟,因此所需的计算时间很短。
以下宽带噪声源模型对局部声功率执行下列操作:
- Curle 噪声源模型
- 估计偶极源产生的每单位表面声音
- Goldstein 轴对称噪声源模型
- Proudman 噪声源模型
- 估计四极源产生的每单位体积声音
- Lilley 噪声源模型
- 线性欧拉方程 (LEE) 噪声源模型
- 估计湍流剪切流产生的声音
- 随机噪声产生和辐射 (SNGR) 模型
- 计算合成湍流场
- Lighthill 应力张量
- 估计流体产生的噪声源
- 声学抑制区模型
- 抑制虚假反射
- 网格频率截止分析
- 检查网格是否足够精细,可用于求解相关湍流结构
可以将空气动力生成的主要声源分解到剪切噪声项(表示流体的平均剪切速度和湍流速度分量之间的相互作用)和自发噪声项(表示湍流-湍流相互作用)。
声速
远场声速 是声波在单位时间内传播的距离。
其中:
- 为绝热指数,即,流体恒压热容与恒容热容之比。
- 为通用气体常数。
- 为绝对温度(以开尔文为测量单位)。
在 293 K 下的干燥空气中,声速为 343.2 m/s。
Curle 噪声源模型
Curle 噪声源模型可计算固体上湍流边界层流的噪声(假设湍流各向同性且马赫数较低)。
此模型通常用于空气调节子系统 (AHS) 应用,其中包括旋转部件(如风机)、热交换器、消声器、分配管和壁面封闭空间。
Curle 模型表示偶极噪声源,即来自作用于流体上的固体边界中波动表面压力的噪声。具体地说,此模型将计算对体表面的单位面积声功率的局部贡献。
根据 Curle [884],声密度可根据局部贡献写为:
其中:
- 为声密度。
- 为远场声速。
- 为发射时间。
- 为表面压力。
- 为远场中的位置,其中 和 是生成的声音的典型波长,因此 位于每个偶极噪声源的辐射场中。
- 为固体边界表面上的面形心位置。
- 为源和远场位置之间的物理距离。
- 为向外壁面法向。
基于小扰动和绝热问题假设:
其中, 为恒定压力 ( ) 和恒定体积 ( ) 下的比热比。
根据扰动的等熵,声压和密度扰动的变化可以写为:
然后,对于声学密度的 Eqn. (4660) 将成为以下声压方程:
在远场中,固体表面沿 的每单位表面定向声强根据以下方程粗略计算而得:
其中:
- 为声学相关性区域。
- 是 与壁面法向 之间的夹角,因此
可根据以下方程计算对每单位表面声功率的局部贡献的度量(即表面声功率,简称为 SAP):
然后,可以通过以下方法计算表面声功率:
可以将该关系重写为包括声相关性区域公式和表面压力 的均方时间导数,如下所示:
其中,对于 和 Hinze[896] 提供了:
且
- 为壁面压力波动。
- 为均方湍流速度。
- 为湍动能。
- 为壁面剪切应力。
- 为远场密度。
可以为使用雷诺平均纳维-斯托克斯 (RANS) 湍流模型(这些模型可提供湍动能和壁面剪切应力)的稳态和非稳态模拟激活 Curle 模型。
可以使用量纲单位 () 和 dB 报告每单位表面的声功率:
其中, 为参考声功率。
Goldstein 轴对称噪声源模型
Goldstein 模型基于 Lighthill 的理论,用于在局部均匀和各向异性湍流的假设下预测湍流剪切流的空气动力噪声。
通过消除雷诺应力的时空相关性的 Ribner 假设,Goldstein [895] 将 Ribner 轴对称湍流模型 [910] 广义化。
此模型可计算轴对称湍流射流中各向异性湍流的每单位体积的局部噪声贡献。
可通过以下方程计算对每单位网格单元体积的总声功率的局部贡献:
其中, 和 为接收器位置的径向和角度坐标(假设接收器距离流体足够远)。 为每单位体积射流的定向声强:
为已修正对流因子:
假设湍流局部均匀,声强将分解到剪切噪声和自发噪声(无耦合项):
其中:
- 为远场密度。
- 为远场声速。
湍流的各向异性结构作用通过以下参数显示:
其中, 和 为纵向和横向相关长度(二者不相等)。纵向湍流速度 和横向湍流速度 在各个方向上都不相等,因此 且 。在极限情况下,各向同性湍流和方向性表达式变为与 Ribner 模型的这些表达式完全相同,因此 且 。
纵向湍流速度 和横向湍流速度 使用以下关系进行计算:
其中:
- 为湍流时间尺度 。
- 为湍流长度尺度 。
为湍动能,而 为耗散率。
在 Simcenter STAR-CCM+ 中,可以使用量纲单位 ( ) 和 dB 报告每单位体积的总声功率:
其中, 为参考声功率。
另请参见 Bechara 等人的 [878]。
Proudman 噪声源模型
像 Goldstein 模型一样,Proudman 噪声源模型可计算每单位体积的声功率,且声音来自四极,例如,风机叶片周围的区域。此模型已用于空气调节子系统 (AHS) 应用,包括旋转部件(如风机)、热交换器和分配管。Proudman 模型假设各向同性湍流。
Proudman 认为各向同性湍流会产生噪声。对于不可压缩近流中的各向同性湍流,根据 Proudman 高雷诺数模型,每单位体积的 AP(声功率)为:
其中:
- 为与纵向速度相关性关联的常数。
- 为速度分量之一的均方根。
- 为速度的纵向积分长度尺度。
- 为远场密度。
- 为远场声速。
不同的研究人员发现 值有所不同,范围为 0.629 到 13。Simcenter STAR-CCM+ 使用 Sarkar 和 Hussaini 提出的重新缩放常数 [912]。
在 Proudman 发表的论文 [909] 中,含能涡的特征速度 可以写为:
根据湍流速度比例和湍流长度尺度,因单位体积的各向同性湍流而产生的局部声功率 ( ) 将变为:
且:
其中:
- 为远场密度。
- 为湍流速度。
- 为湍流长度尺度。
- 为湍流时间尺度。
- 为远场声速。
重新缩放常数 基于 Sarkar 和 Hussaini 针对各向同性湍流进行的直接数值模拟 [912]。
可以使用量纲单位 ( ) 和 dB 报告每单位体积的总声功率:
其中, 为参考声功率。
Lilley 噪声源模型
Lilley 噪声源模型可计算波动速度流场的四极源的湍流剪切流噪声。
适用于局部剪切效应占主导的问题,如围绕固体的流体和通道中的剪切流。此模型可计算气动声学声源的位置和强度。此模型仅适用于稳态模拟。
Lilley 噪声源模型兼容耦合流体和分离流模型。计算成本(尤其是 CPU 时间)取决于为随机噪声产生和辐射 (SNGR) 模型提供的以下两个属性的输入:实现的数量和傅立叶模式数。Lilley 噪声源模型会计算以下三项:Lilley 自发噪声源、Lilley 剪切噪声源和 Lilley 总噪声源。
Lilley 源项可用于使用雷诺平均纳维-斯托克斯 (RANS) 湍流模型计算得出的稳态求解。如同围绕固体的流体和通道中的剪切流一样,RANS 模型是可提供湍流长度尺度和湍流时间尺度(以局部剪切效应为主)的唯一类型。
Lilley 方程可以写为:
其中, 为声速, 为应力张量, 表示熵波动和流体粘度效应。
对于无热传递或燃烧的问题,熵波动可以忽略不计。对于高雷诺数流体,粘性效应也可以忽略不计。因此,方程右侧通常忽略这些项。则 Eqn. (4683) 变为:
其中:
为参考压力。
通过假定流体满足小扰动假设,流体将局部线性化,如下所示:
其中, 为平均速度场, 为湍流速度场。Eqn. (4685) 右侧可以扩展如下:
其中, 表示平均流形状变化,自发噪声项 包含湍流(波动)速度分量的效应,剪切噪声项 包含平均剪切流和湍流速度分量之间的相互作用。
将根据稳态 RANS 求解和湍流速度分量提供的平均速度场计算 Lilley 方程的噪声源项。这些分量由 Bailly 和 Juve [877]、Bechara 等人[878] 以及 Kraichnan [900] 提出的合成湍流法生成。
线性欧拉方程 (LEE) 噪声源模型
线性欧拉方程 (LEE) 会考虑任何剪切平均流中的折射和对流影响。与 Lilley 方程相比,该方程适用的条件范围更大,其中关联源项是波动速度流场的非线性函数。请参见 [878]。
| 注 | 此模型仅用于噪声源,而不用于求解声波传播。 |
此模型仅适用于稳态模拟。如同 Lilley 方程一样,LEE 噪声源模型可计算 LEE 自发噪声源、Lilley 剪切噪声源和 Lilley 总噪声源。
欧拉方程的线性化形式 [878] 衍生自非线性欧拉方程。通过将小湍流扰动和声学分量叠加到平均流上,可以实现线性化形式,如下所示:
其中,声学分量 、 、 小于平均分量 、 、 和湍流分量 、 、 。
将变量分解纳入 Eqn. (4692) 并考虑声扰动为恒熵的假设:
且湍流密度波动 ( ) 可以忽略不计,速度分量的线性欧拉方程将变为:
第二组项包括负责声音产生的源项。
可以将空气动力生成的主要声源分解到剪切噪声项 (表示流体的平均剪切速度和湍流速度分量之间的相互作用)和自发噪声项 (表示湍流-湍流相互作用):
湍流速度分量由随机噪声产生和辐射模型合成。
与 Lilley 方程中的源项类似,线性欧拉方程中的源项可用于使用雷诺平均纳维-斯托克斯 (RANS) 湍流模型计算得出的稳态求解,该模型可提供湍流长度尺度和湍流时间尺度。
随机噪声产生和辐射 (SNGR) 模型
SNGR 模型的范围是计算合成湍流场。
可使用随机傅立叶模式生成时间-空间湍流速度场。此方法称为随机噪声产生和辐射 (SNGR) 模型,由 Kraichnan [900] 和 Karweit 等人[898] 提出,之后得到了进一步发展,具体贡献者包括 Bailly 和 Juve [877]、Bechara 等人[878]。在 Simcenter STAR-CCM+ 中,SNGR 方法需要用户输入 Lilley 噪声源模型的两个属性:实现的数量和傅立叶模式数。请参见 Lilley 和 LEE 噪声源属性。
考虑在位置 的给定点处进行均匀各向同性湍流场的三维傅立叶分解:
其中, 为湍流速度场, 为波矢量, 为虚部单位,且 。
此傅立叶积分可以转换为 个傅立叶模式的有限总和:
其中,、 和 分别为与波矢量 关联的第 个傅立叶模式的幅值、相位和方向单位矢量。
计算每个模式的幅值 ,使湍动能 对应于均匀各向同性湍流的 von Karman-Pao 能谱:
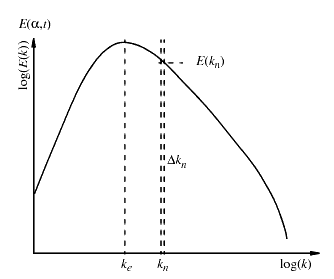
其中, 为模式幅值, 为 下该谱中的小间隔。
von Karman-Pao 能谱的表达式可以写为:
其中:
- 为波数。
- 为 Kolmogorov 波数。
- 为对应于湍动能的速度波动的均方根值。
- 为数值常数。
- 为对应于该谱中达到峰值的大多数含能涡的波数。
Lighthill 方程
Lighthill 方程是一个不均匀波方程,通过使用纳维-斯托克斯方程模拟可压缩流体衍生声场(Lighthill 模拟 [901])。在 Lighthill 方程中,声场由称为 Lighthill 湍流应力张量的二阶张量表示。
根据分量形式,流体质量和动量守恒方程为:
其中:
- 为密度。
- 和 为速度分量。
- 为应力张量。(4703)
其中
- 为流场的热力学压力,即,工作压力。
- 为克罗内克增量。
- 为粘性应力张量。(4704)
使用爱因斯坦标记法,Lighthill 方程可以写为:
其中, 为声场的“Lighthill 湍流应力张量”。
将 Eqn. (4704) 代入 Eqn. (4706) 可得出:
其中, 为远场密度。
在层流中,粘性应力张量由以下公式给出:
在湍流中,粘性应力张量由以下公式给出:
其中,有效粘度为 ,即层流粘度与湍流粘度之和。
在无粘性流中,粘性应力张量为 。
Eqn. (4707) 中的每个源项表示声音产生期间的一个重要作用,如下所示:
- 描述流体的非稳态对流(或雷诺应力)
- 描述声剪切
- 描述非线性声学产生处理
网格频率截止公式
对稳态求解执行网格频率截止分析的主要价值是,在瞬态计算之前确定所选网格的分辨率是否足以在相关频率范围内捕捉湍流结构。
Mendonça [907] 证明,给定网格单元尺寸 和局部湍动能 ,网格捕捉的最小湍流涡结构长度尺度为 ;其关联的各向同性波动速度为 。因此,由局部网格间距 合理求解的最大频率 为:
表示平均湍流结构所含的平均湍动能。最常用的 RANS 湍流模型可直接求解 传输方程。 传输方程直接从非稳态纳维-斯托克斯方程中衍生得出,因此包含所有重要机制的贡献:对流、扩散、生成和耗散。只要捕捉到平均流特征, 求解就趋向合理地独立于网格。
此度量优先用于衍生自湍流时间尺度的表达式,即,动能与其耗散率之比 。这可更好地表示耗散尺度,在频率含量和能含量中,这些尺度比人类听力范围或峰值灵敏度高多个数量级。
由于此度量衍生自稳态求解,因此存在一些固有的限制。不考虑与时间变化大尺度运动(通过网格对流传热)关联的频率(例如,涡流脱落)。相反,其用途是近似在 RANS 中建模和在大涡模拟中求解的湍流尺度的频率。换言之,此度量更适用于宽带励磁,而非窄带励磁。
网格频率截止度量已应用于低马赫数流的典型工业应用。