流和能量的壁面处理

流和能量模型的壁面处理可为壁面处的流和能量求解器提供边界条件。

以简化方式衍生壁面处理提供的边界条件，考虑以下 2D 域，其中壁平行于 $x$ 方向，壁面法向是 $y$ 方向：

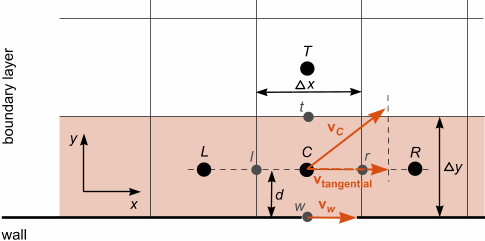
对于没有外力的稳态流体，标量 $ϕ$ 的传输方程的差分形式给定如下：

图 1. EQUATION_DISPLAY

\frac{\partial}{\partial x} (ρ v ϕ) = \frac{\partial}{\partial y} (Γ \frac{\partial ϕ}{\partial y}) + S_{ϕ}

(1621)

其中：

将此方程与近壁网格单元的体积进行积分可以给出以下方程：

图 2. EQUATION_DISPLAY

[{(ρ v ϕ)}_{r} - {(ρ v ϕ)}_{l}] Δy = [{(Γ \frac{\partial ϕ}{\partial y})}_{t} - {(Γ \frac{\partial ϕ}{\partial y})}_{w}] Δx + S_{ϕ} ΔxΔy

(1622)

其中：

对于动量 ( $ϕ = u, v$ ) 和能量 ( $ϕ = E$ )，壁面法向梯度 ${(Γ \frac{\partial ϕ}{\partial y})}_{w}$ 分别对应于壁面剪切应力 $τ_{w}$ 和壁面热通量 ${\dot{q}}_{w} ″$ 。

壁面剪切应力

对于层流，壁面剪切应力计算为：

图 3. EQUATION_DISPLAY

τ_{w} = μ {[{(\nabla v_{tangential})}_{C} + {(\nabla v_{tangential})}_{C}^{T}] - \frac{2}{3} {(\nabla\cdot v_{tangential})}_{C} I} n

(1623)

其中：

图 4. EQUATION_DISPLAY

v_{tangential} = (v_{C} - v_{w}) - [(v_{C} - v_{w}) \cdot n] n

(1624)

和

壁面剪切力定义如下：

图 5. EQUATION_DISPLAY

f_{w} = {- τ}_{w} A

(1625)

其中 $τ_{w}$ 为壁面剪切应力， $A$ 为边界面面积。

对于湍流，壁面剪切应力必须考虑因为近壁区域内湍流混合而增加的剪切应力。应用的方法基于壁面摩擦速度 $u_{τ}$ ，根据该速度，壁面剪切应力计算为：

图 6. EQUATION_DISPLAY

τ_{w} = ρ u_{τ}^{2}

(1626)

壁面摩擦速度 $u_{τ}$ 根据选定的湍流建模方法进行计算，参见湍流模型的壁面处理。

对于层流，壁面热通量矢量计算为：

图 7. EQUATION_DISPLAY

{\dot{q}}_{w} ″ = - k {(\nabla T)}_{C}

(1627)

其中：

然后，从壁面热通量矢量获得壁面热通量，如下所示：

图 8. EQUATION_DISPLAY

{\dot{q}}_{w} ″ = | {\dot{q}}_{w} ″ |

(1628)

对于湍流，壁面热通量计算为：

图 9. EQUATION_DISPLAY

{\dot{q}}_{w} ″ = ρ C_{p} u_{*} \frac{{\hat{T}}_{C} - T_{w}}{{\hat{T}}_{C}^{+}}

(1629)

其中 $C_{p}$ 是比热。

速度比例 $u_{*}$ 和无量纲 RANS 平均/LES 过滤的网格单元温度 ${\hat{T}}_{C}^{+}$ 由选定湍流建模方法的壁面处理给出。参见湍流模型的壁面处理。