粗糙壁面的壁面处理

粗糙度效应是各工程应用程序中的一个严重问题。即使很小的表面缺陷也可能会在速度场中产生明显干扰，并更改流行为，从而影响产品的性能。在大多数情况下，粗糙度结构过小而无法由网格求解。因此，使用壁面粗糙度模型。

通常，通过将内边界层的对数层靠近壁面来对壁面粗糙度效应建模。Simcenter STAR-CCM+ 提供了两种方法来体现这种效应 - 粗糙和粗糙位移原点。

粗糙

粗糙方法使用数据相关性来计算粗糙度函数 $f$ ，该函数可减少速度的壁面函数和温度的壁面函数中的对数律偏移 $E$ 。

粗糙度函数 $f$ 是粗糙度参数 $R^{+}$ 的函数，定义为：

图 1. EQUATION_DISPLAY

R^{+} = \frac{r ρ u_{*}}{μ}

(1639)

其中：

$r$ 是等效的砂粒粗糙度高度和模型系数。
$ρ$ 为密度。
$u_{*}$ 是速度比例。
$μ$ 为动力粘度。

粗糙度函数 $f$ 基于在 [391] 中给出的表达式，并定义为：

图 2. EQUATION_DISPLAY

f = {\begin{matrix} 1 & {; R}^{+} \leq R_{smooth}^{+} \\ {[B (\frac{R^{+} - R_{smooth}^{+}}{R_{rough}^{+} - R_{smooth}^{+}}) + C R^{+}]}^{a} & {; R}_{smooth}^{+} < R^{+} < R_{rough}^{+} \\ B + C R^{+} & {; R}^{+} > R_{rough}^{+} \end{matrix}

(1640)

且：

图 3. EQUATION_DISPLAY

a = \sin [\frac{π}{2} \frac{\log (R^{+} / R_{smooth}^{+})}{\log (R_{rough}^{+} / R_{smooth}^{+})}]

(1641)

其中：

$B$ 和 $C$ 是模型系数。
$R_{smooth}^{+}$ 和 $R_{rough}^{+}$ 分别为对应于完全平滑表面和完全粗糙表面的粗糙度参数，是模型系数。

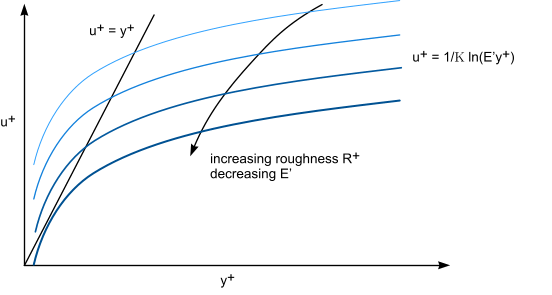
对于 $R^{+}$ 的高值，对数分布可以停止与子层中假定的线性分布相交，如下图所示：

如果此事件在完全粗糙的区域 ( $R^{+} > R_{rough}^{+}$ ) 中发生，则不会出现问题，因为子层不相关。如果这些曲线不与过渡粗糙度区域 ( $R_{smooth}^{+} < R^{+} < R_{rough}^{+}$ ) 相交，则 Simcenter STAR-CCM+ 使用对数分布，条件是 $u^{+}$ 必须从未小于零。

对于所有湍流模型（只要使用默认壁面处理），如果粗糙度高度大于壁面相邻网格单元的壁面距离 ( $R^{+} > y^{+}$ )，此建模方法在物理上就没有意义。在这种情况下，Simcenter STAR-CCM+ 会限制局部粗糙度高度，并将其设为等于壁面相邻网格单元的壁面距离 ( $R^{+} = y^{+}$ )。

粗糙位移原点

粗糙位移原点方法使用名为原点位移的模型（[389]、[393]）。此模型将使粗糙度高度上方的边界层原点移位，并对速度、温度、湍流耗散率和比耗散率使用特定的壁面函数。

速度

对于标准壁面函数，无量纲速度

u^{+}

描述为：

图 4. EQUATION_DISPLAY

u^{+} = \frac{1}{κ} \log (\frac{y_{e f f}}{y_{0}}) = \frac{1}{κ} \log (\frac{y^{+} + y_{0}^{+}}{y_{0}^{+}})

(1642)

且：

图 5. EQUATION_DISPLAY

y_{0}^{+} = {\begin{matrix} \begin{matrix} 0.56 {(R^{+} / R_{s m o o t h}^{+})}^{2.5} \\ 0.63 ζ (R^{+}) + 0.028 R^{+} \end{matrix} & \begin{matrix} {; R}^{+} < R_{s m o o t h}^{+} \\ ; R_{s m o o t h}^{+} \leq R^{+} \leq R_{r o u g h}^{+} \end{matrix} \\ 0.031 R^{+} - 0.27 & ; R^{+} > R_{r o u g h}^{+} \end{matrix}

(1643)

图 6. EQUATION_DISPLAY

ζ (R^{+}) = \sin [π {(\frac{R^{+} - 20}{70})}^{0.9}]

(1644)

其中：

$κ$ 为冯·卡门常数。
$y_{e f f}$ 为边界层的有效原点。
$y_{0}$ 为边界层的位移原点。
$y^{+}$ 由 Eqn. (1584) 给出。
$y_{m}^{+}$ 是指粘性子层满足对数层求解时所处的点，可使用牛顿-拉夫森法迭代计算。

在 Reichardt 定律修正中，原点位移方法与混合壁面函数结合使用，如下所示：

图 7. EQUATION_DISPLAY

u^{+} = \frac{1}{κ} \log (1 + κ y^{+}) + C [1 - \exp (- \frac{y^{+}}{y_{m}^{+}}) - \frac{y^{+}}{y_{m}^{+}} \exp (- b y^{+})]

(1645)

且：

图 8. EQUATION_DISPLAY

C = \frac{1}{κ} \ln (\frac{1}{κ y_{0}^{+}})

(1646)

其中， $b$ 由 Eqn. (1601) 给出。

为确保混合 Reichardt 公式在

R_{r o u g h}^{+} < R^{+} < R_{s m o o t h}^{+}

，Simcenter STAR-CCM+ 剪切

u^{+}

时生成合理的速度分布：

u^{+} = {\begin{matrix} \frac{1}{κ} \log (\frac{y^{+} + y_{0}^{+}}{y_{0}^{+}}) & {; y}_{0}^{+} > y_{m}^{+} \\ u_{s m o o t h}^{+} & {; \begin{matrix} R \end{matrix}}^{+} < R_{s m o o t h}^{+} \end{matrix}}

(1647)

温度

对于标准壁面函数和混合壁面函数，无量纲温度

T^{+}

的分布定义为：

图 9. EQUATION_DISPLAY

T^{+} = \exp (- Γ^{'}) \Pr y^{+} + \exp (- \frac{1}{Γ^{'}}) \Pr_{t} [\frac{1}{κ} \ln (\frac{y^{+} + y_{0}^{+}}{y_{0}^{+}}) + P]

(1648)

其中：

$\Pr$ 为普朗特数，由 Eqn. (1141) 给出。
$\Pr_{t}$ 为湍流普朗特数。
$P$ 由 Eqn. (1610) 给出。

$Γ^{'}$ 是混合函数，定义如下：

图 10. EQUATION_DISPLAY

Γ^{'} = \frac{0.01 {[\Pr (y^{+} + y_{0}^{+})]}^{4}}{1 + 5 \Pr^{3} (y^{+} + y_{0}^{+})}

(1649)

湍流耗散率

对于标准壁面函数和混合壁面函数，无量纲湍流耗散率

ε^{+}

设为：

图 11. EQUATION_DISPLAY

ε^{+} = γ \frac{2 k^{+}}{{(y^{+})}^{2}} Y_{e} + (1 - γ) \frac{1}{κ y^{+}}

(1650)

其中：

图 12. EQUATION_DISPLAY

Y_{e} = \frac{y^{2}}{{(\frac{y}{2.236} + {(y_{0}^{+})}^{3} \frac{μ}{{ρ u}_{*}})}^{2}}

(1651)

和：

$γ$ 由 Eqn. (1597) 给出，此外还要求 $R^{+} > R_{rough}^{+}$ 时 $γ = 0$ ，其中 $R_{rough}^{+}$ 是完全粗糙面的粗糙度参数。完全粗糙面是粗糙度效应过大以致壁面附近不存在可见粘性流行为的表面。
$k^{+}$ 由 Eqn. (1590) 给出。
$y$ 为与壁面的距离。
$u_{*}$ 由 Eqn. (1595) 给出。

比耗散率

对于标准壁面函数和混合壁面函数，无量纲比耗散率

ω^{+}

的公式取决于壁面处理，并计算为壁面粗糙度的函数，如 Wilcox [395] 所述：


壁面处理	$ω^{+}$
低 $y^{+}$	图 13. EQUATION_DISPLAY $ω^{+} = S_{r}$ (1652)
全 $y^{+}$	图 14. EQUATION_DISPLAY $ω^{+} = γ S_{r} + (1 - γ) \frac{1}{κ \sqrt{C_{μ}}}$ (1653)

且：

图 15. EQUATION_DISPLAY

S_{r} = {\begin{matrix} {(\frac{50}{R^{+}})}^{2} & ; 5 \leq R^{+} \leq 25 \\ \frac{100}{R^{+}} & {; R}^{+} \geq 25 \end{matrix}

(1654)

和 $C_{μ}$ 是 K-Omega 模型 - 模型系数。

模型系数


	$r$	$B$	$C$	$R_{smooth}^{+}$	$R_{rough}^{+}$
粗糙	0	0	0.253	2.25	90
粗糙位移原点	0	-	-	20	90