Wall Boiling Model Reference

The wall boiling model predicts the amount of wall superheat, which is the amount the wall temperature exceeds the saturation temperature, as well as the axial and radial distribution of vapor. For more information, see Boiling.

表 1. Wall Boiling Model Reference
Theory	See Wall Boiling.
Provided By	[Phase Interaction] Model Selection > Optional Models
Example Node Path	[Phase Interaction] > Models > Wall Boiling
Requires	A Eulerian Multiphase simulation with the following models activated: Material: Multiphase, Multiphase Interaction (Selected automatically) Multiphase Model: Eulerian Multiphase (EMP), Gradients (Selected automatically) Optional Models: Phase Coupled Fluid Energy Viscous Regime: Laminar or Turbulent Space: Three Dimensional, Axisymmetric, or Two Dimensional Time: Steady or Implicit Unsteady A minimum of two Eulerian phases: one liquid phase and one gas phase. In the liquid phase, the following phase models activated: Material: Liquid or Multi-Component Liquid Energy: Segregated Fluid Temperature or Segregated Fluid Enthalpy Reaction Regime: Non-reacting (applies to multi-component phases only) Equation of State: Constant Density Optional Models: Wall Distance In the gas phase, the following models activated: Material: Gas or Multi-Component Gas Energy: Segregated Fluid Temperature or Segregated Fluid Enthalpy Reaction Regime: Non-reacting (applies to multi-component phases only) Equation of State: Constant Density Optional Models: Wall Distance A Continuous-Dispersed Topology or Multiple Flow Regime Topology phase interaction is required. In the phase interaction, the following models activated: Optional Models: Interphase Mass Transfer Interphase Mass Transfer Rate: Boiling Mass Transfer Rate (for a Continuous-Dispersed phase interaction) or Boiling/Condensation (for a Multiple Flow Regime phase interaction) Optional Models: Wall Boiling
Properties	Key properties are: Relaxation Factor. See Wall Boiling Properties.
Activates	Physics Models	Wall Bubble Nucleation See Wall Bubble Nucleation Properties. Wall Transient Conduction See Wall Transient Conduction Properties.
	Model Controls (child nodes)	Wall Dryout Area Fraction See Wall Dryout Area Fraction Properties.
	Boundary Inputs	See Boundary Settings.
	Field Functions	See Field Functions.

Wall Boiling Properties

Relaxation Factor: Adjusts the model sensitivity. Reduce it to improve convergence.

Wall Boiling Model Controls

The following child nodes are provided:

Wall Dryout Area Fraction: The wall dryout area fraction specifies how much of the heat flux that is applied at the wall is directed towards the vapor convection, as opposed to liquid convection and evaporation. It can be used to improve robustness during initial convergence, or for indicating the onset of Departure from Nucleate Boiling (DNB) conditions in converged solutions.
For more information, see Wall Dryout Area Fraction.

Wall Dryout Area Fraction Properties

Method

Basic Wall Dryout Area Fraction

Defines the area fraction as zero until the volume fraction of the vapor near the wall exceeds a specified value. It then transitions the area fraction to unity as the vapor volume fraction approaches unity.

To reduce grid-dependency, the near-wall volume fraction that is used for the area fraction calculation can optimally be defined as an average over a prescribed thickness of a notional bubbly layer next to the wall.

This method is the default.

Constant, Field Function, Table, and User Code

Standard methods provided for user-specified values.

Wall Dryout Breakpoint

The vapor volume fraction at which point heat transfer to the vapor phase begins (see Eqn. (2123)). The default value is 0.9.

This property is available for the Basic Wall Dryout Area Fraction method only.

Bubbly Layer Relaxation Factor

Controls the update of the Bubbly Layer Volume Fraction that is used by the dryout model. It helps convergence behavior once the dryout criterion has been exceeded. The default value is 0.5.

Bubbly Layer Option

Defines the thickness of the layer that is used for averaging volume fraction in the dryout criterion.

Wall Cell
The value that is computed at the cell center next to the wall represents the entire bubbly layer. This means the cell-center volume fraction is used in the dryout criterion. This is the default setting.
Fixed Number of Diameters
The bubbly layer thickness is defined by the local bubble departure diameter multiplied by this value.
Fixed Yplus
The bubbly layer thickness is defined by the wall turbulence length scale for the vapor phase multiplied by this value.

Wall Bubble Nucleation Properties

The following child nodes are provided:

Nucleation Site Number Density
Bubble Departure Diameter
Bubble Departure Frequency
Lift Off Diameter (only if the Adaptive Multiple Size-Group (AMUSIG) Model or an S-Gamma Model is selected in the dispersed phase)

Nucleation Site Number Density Properties

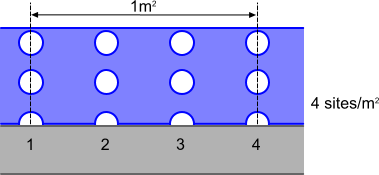
The nucleation site number density determines the number of locations on the heated surface where bubbles form, per unit area.

This is the leading factor determining the evaporation rate in a mechanistic model of subcooled boiling (see Eqn. (2110)). The diagram below illustrates this parameter:

Method

The options for calculating the nucleation site number density.

Lemmert-Chawla
Hibiki-Ishii
Li
User-Defined: Constant, Field Function, Table, or User Code.

Lemmert-Chawla Properties

The Lemmert Chawla model ([499]) is a correlation with wall superheat and is the default model, recommended for initial studies on the grounds of robustness. The default settings assume that the number of active nucleation sites varies with the wall superheat to the power of 1.805. This value is used within the Tolubinsky and Kostanchuk model for calculating bubble departure diameter, for example for modeling forced convection, subcooled boiling of water at 45 bar.

Calibration Constant A

A

in Eqn. (2128). The default value of 1.805 is chosen according to Kurul and Podowski ([494]).

Calibration Constant B

B

in Eqn. (2128). The default value is 0.0.

Maximum Superheat

Δ T_{m a x}

in Eqn. (2127). Sets the upper limit for the wall superheat value that is passed to this submodel, which prevents overflow during initial convergence. Make sure that this limit does not affect the value of wall superheat predicted in the converged solution. The default value is 25.0 delta K.

Reference Nucleation Site Number Density

n_{0}^{"}

in Eqn. (2128). The default value is 12366.44783 / m².

Reference Wall Superheat

Δ T_{0}

in Eqn. (2128). The default value is 1.0 K.

Nucleation Site Density Limiting

At high pressures, the calculated values for nucleation site density can become unphysical. To keep the calculated nucleation site density within physical limits, a correction can be applied. This option is enabled by default.

See Nucleation Site Number Density Limiting.

Occupancy Probability

Specifies the probability that the nucleation site is occupied by a growing bubble. This value is

f_{A T}

in Eqn. (2145). The default value is 0.2.

Hibiki-Ishii Properties

The Hibiki Ishii model is a more advanced nucleation site number density model. It is applicable for pressures up to 198 bar. Use the Hibiki Ishii model with the Kocamustafaogullari model for bubble departure diameter.

The model has the following characteristics:

It considers a boundary condition for wall superheating.
It is validated against numerous sets of experimental data.
It has a wide range of applicability in terms of mass flow, pressure, and contact angle.

If you use a working fluid other than water, adjust the Wall Contact Angle. If you know average cavity density and the cavity length scale values for the working surface, adjust these also.

Maximum Superheat

Sets the upper limit for the wall superheat value that is passed to this submodel (see Eqn. (2129)), which prevents overflow during initial convergence. Make sure that this limit does not affect the value of wall superheat predicted in the converged solution.

Wall Contact Angle

Data that you define for your working fluid. A nominal value at room temperature is required. The default of 0.722 radians (41.37^o) is an approximate value for water systems (see Eqn. (2132)).

Average Cavity Density

The average number of nucleation sites per unit area, which is used when calculating the nucleation site number density (see Eqn. (2132)). This can be tuned to suit a particular surface finish.

Wall Contact Angle Scale

Reference value used in the model to account for dependence on Wall Contact Angle (see Eqn. (2132)). The standard value for most applications is 0.722 radians (41.37^o).

Cavity Length Scale

Value that is used when calculating the nucleation site number density (see Eqn. (2132)). This can be tuned to suit a particular surface finish.

Density Function Constant C0, C1, C2, and C3

Values used in the model to account for the pressure, which is used when calculating nucleation site number density (see Eqn. (2134)). The standard values for most applications are -0.1064, 0.48246, -0.22712, and 0.05468.

Nucleation Site Density Limiting

At high pressures, the calculated values for nucleation site density can become unphysical. To keep the calculated nucleation site density within physical limits, a correction can be applied. This option is enabled by default.

See Nucleation Site Number Density Limiting.

Occupancy Probability

Specifies the probability that the nucleation site is occupied by a growing bubble. This value is

f_{A T}

in Eqn. (2145). The default value is 0.2.

Li Properties

The Li model is based on a parametric analysis of existing experimental data. It is a function of three variables: wall superheat, pressure, and contact angle. This model is applicable for pressures ranging from 0.101 MPa–19.8 MPa.

The Li model has the same range of applicability pressure and wall superheat as the Hibiki-Ishii model. It is validated against numerous sets of experimental data, and has a wide range of applicability in terms of mass flow, pressure, and contact angle.

If you use a working fluid other than water, you are requires to adjust the Wall Contact Angle. If you know the average cavity density value for the working surface, you are advised to adjust that also.

If you are modeling subcooled boiling, you are advised to use the Li model.

Nucleation Site Density Limiting: When activated, applies nucleation site density limiting. At high pressures, the calculated values for nucleation site density can become unphysical. To keep the calculated nucleation site density within physical limits, a correction can be applied. For more information, see Nucleation Site Number Density Limiting. This property is activated by default.

Occupancy Probability: Specifies the probability of the nucleation site being occupied by a growing bubble. This value is $f_{A T}$ in Eqn. (2145). The default value is 0.2.

Average Cavity Density: The average number of nucleation sites per unit area, which is used when calculating the nucleation site number density. This is $n_{0}$ in Eqn. (2138). This can be adjusted to suit a particular surface finish.

Wall Contact Angle: The wall contact angle that you define for your working fluid. This is $θ_{0}$ in Eqn. (2140). A nominal value at room temperature is required. The standard value for most applications is 0.722 radians (41.37^o).

Zero Contact Angle Temperature: The zero contact angle temperature, which is used to account for dependence on Wall Contact Angle. This is $T_{0}$ in Eqn. (2140).

Contact Angle Reference Temperature: The reference temperature, which is used to account for dependence on Wall Contact Angle. This is $T_{c}$ in Eqn. (2140).

Maximum Superheat: $Δ T_{m a x}$ in Eqn. (2127). Sets the upper limit for the wall superheat value that is passed to this submodel. Prevents overflow during initial convergence. Make sure that this limit does not affect the value of wall superheat that is predicted in the converged solution. The default value is 25.0 K.

Bubble Departure Diameter Properties

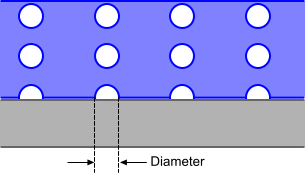
The bubble departure diameter determines the diameter of the bubble at the instant it leaves the nucleation site.

This is the second of the three factors used to determine the evaporation rate in subcooled boiling (see Eqn. (2110)). The diagram below illustrates this parameter:

Method

The options for calculating the bubble departure diameter.

Tolubinsky Kostanchuk
Kocamustafaogullari
Unal
User-Defined: Constant, Field Function, Table, or User Code.

Tolubinsky Kostanchuk Properties

The Tolubinsky Kostanchuk model is a correlation against liquid subcooling and is the default model that is recommended for initial studies on the grounds of robustness. It matches the default Lemmert Chawla model for nucleation site number density.

Reference Diameter: Reference diameter that is used when calculating the bubble departure diameter (see Eqn. (2150)), as determined by experiment for a given subcooling of 45K.
Reference Diameter Subcooling: Reference diameter subcooling (that is, the difference between the saturation temperature and liquid temperature for the reference diameter) used when calculating the bubble departure diameter at the given value of subcooling (see Eqn. (2150)).
Minimum Diameter: Sets the lower limit for the bubble departure diameter. This setting makes sure that the result is within plausible limits.
Maximum Diameter: Sets the upper limit for the bubble departure diameter. This setting makes sure that the result is within plausible limits.

Kocamustafaogullari Properties

The Kocamustafaogullari model is more recent, more general and based on a force balance with an adjustment for pressure dependence. This model must be used whenever the Hibiki Ishii model is selected for nucleation site number density.

Calibration Constant: Calibration constant (see Eqn. (2152)). The standard value is 1.5126x10^-3 m/radian (2.64x10^-5 m/degree).
Wall Contact Angle: Data that you specify for your working fluid. A nominal value at room temperature is required. The default of 0.722 radians (41.37^o) is an approximate value for water systems (see Eqn. (2152)).
If you use a working fluid other than water, you can adjust the Wall Contact Angle as required.

Unal Properties

The Unal model is suitable for both low-pressure and high-pressure boiling scenarios. No parameter tuning is required. You can obtain better predictions if you also model the bubble size distribution, breakup, and coalescence.

Reference Diameter Subcooling: Reference diameter subcooling (that is, the difference between the saturation temperature and liquid temperature for the reference diameter) used when calculating the bubble departure diameter at the given value of subcooling. This value is $Δ T_{s u b}$ in Eqn. (2153).
Minimum Diameter: Sets the lower limit for the bubble departure diameter. This setting makes sure that the result is within plausible limits.
Maximum Diameter: Sets the upper limit for the bubble departure diameter. This setting makes sure that the result is within plausible limits.

Bubble Departure Frequency Properties

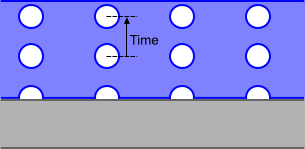
The bubble departure frequency determines how many bubbles leave a nucleation site per second.

This is the last of three key factors determining the evaporation rate in subcooled boiling (see Eqn. (2110)). The diagram below illustrates this parameter:

Method

The options for calculating the bubble departure frequency.

Cole: This frequency is equivalent to a terminal velocity scale over bubble departure diameter, and the overall evaporation rate is calibrated around this assumption (see Eqn. (2155)). There are no adjustable parameters, but you can define an alternative model.
User-Defined: Constant, Field Function, Table, or User Code.

Lift Off Diameter Properties

For the Adaptive Multiple Size-Group (AMUSIG) Model or an S-Gamma Model selected in the dispersed phase, the lift off diameter determines the diameter of the bubbles as provided to the respective particle size distribution model at the wall. Corresponds to $d_{l}$ in Eqn. (2306).

Method

The options for calculating the lift off diameter.

Bubble Departure Diameter: sets the lift off diameter equal to the specified Bubble Departure Diameter.
Field Function: allows you to specify a different wall bubble diameter for the size distribution model than for the wall boiling model.

Wall Transient Conduction Properties

This model corrects the Bubble Induced Quenching Heat Flux so that it uses the temperature of the liquid brought to the wall by the action of the departing bubble. This temperature can be different to the liquid temperature computed at the cell center next to the wall. The correction is taken from a location on the undisturbed liquid phase temperature profile away from the departure site.

Quenching Temperature Option

Defines the location for sampling the liquid temperature profile.

Wall Cell
The liquid temperature at the cell center next to the wall is used as the quenching temperature. This is the default setting.
Fixed Number of Diameters
The liquid temperature is estimated at a location that is specified as a fixed number of the local bubble departure diameter size. You set this in the Fixed Number of Diameters child node.
Fixed Yplus
The liquid temperature is estimated at a location that is specified as a fixed number of wall turbulence length scales for the liquid phase. You set this in the Fixed Y+ child node.

The following child nodes are provided:

Bubble Influence Wall Area Fraction
Bubble Induced Quenching Heat Transfer Coefficient

Bubble Influence Wall Area Fraction Properties

The bubble influence wall area fraction estimates the fraction of the wall area that is affected by the sweep of liquid inflow beneath a departing bubble.

Method

The options for calculating the bubble influence wall area fraction.

Kurul Podowski
User-Defined: Constant, Field Function, Table, or User Code.

Kurul Podowski Properties

The Kurul Podowski model assumes that the wall area influenced by bubble-induced quenching is larger than the nucleation site area, by a specified factor (see Eqn. (2158)).

Area Coefficient: Ratio of nucleation site area density and bubble-influenced wall area density, which is given by (Eqn. (2158)). The default value is 2.0.

Bubble Induced Quenching Heat Transfer Coefficient Properties

When a bubble leaves the heated surface, cooler liquid fills the space that it occupied. The heat transfer during this process is known as quenching heat transfer. The Quenching Heat Transfer Coefficient is used to calculate the quenching heat flux.

Method

The options for calculating the bubble induced quenching heat transfer coefficient.

Del Valle Kenning
User-Defined: Constant, Field Function, Table, or User Code.

Del Valle Kenning Properties

This model calculates the bubble induced quenching heat transfer coefficient using Eqn. (2156).

Wait Coefficient: Proportion of bubble departure cycle period between departure of one bubble and nucleation of the next (see Eqn. (2157)).

Boundary Settings

The following settings are available for wall boundaries.

Phase Conditions

Available for the Unal bubble departure diameter model only, under [Phase Interaction] > Physics Conditions.

Surface Conductivity: The thermal conductivity of the wall surface. This value is $k_{w}$ in Eqn. (2154).
Surface Density: The density of the wall surface. This value is $ρ_{w}$ in Eqn. (2154).
Surface Specific Heat: The specific heat of the wall surface. This value is $c_{p w}$ in Eqn. (2154).

Physics Conditions

Wall Interphase Mass Transfer Option

Activates interphase mass transfer interaction on the wall boundary.

Method	Corresponding Physics Value Nodes
Active Allows wall boiling to occur on this boundary. Under the [Wall Boundary Name] > Phase Conditions node, for each phase in the phase interaction, set the User Wall Heat Flux Coefficient Specification.	None
None Prevents wall boiling from occurring on this boundary. For example, use this option when a boundary is adiabatic.	None

Field Functions

BubblyLayerVolumeFraction: $α_{δ}$ in Eqn. (2122).
BubblyLayerVolumeFractionGradient: ${α^{'}}_{g}$ in Eqn. (2122).
BubbleDepartureDiameter: $d_{w}$ in Eqn. (2150) for the Tolubinsky Kostanchuk model or Eqn. (2152) for the Kocamustafaogullari model.
BubbleDepartureFrequency: $f$ in Eqn. (2155).
BubbleInfluenceWallAreaFraction: $K_{q u e n c h}$ in Eqn. (2158).
BubbleInducedQuenchingHeatTransferCoefficient: $h_{q u e n c h}$ in Eqn. (2156).
BubbleInducedQuenchingTemperatureFactor: $s_{q u e n c h}$ in Eqn. (2117).
BubbleInducedQuenchingTemperatureDistance: $y_{q u e n c h}$ in Eqn. (2117).
Nucleation Site Number Density of [phase interaction]: $n ″$ in Eqn. (2128) for the Lemmert Chawla model, in for the Li model, or Eqn. (2132) for the Hibiki-Ishii model.
WallInterfaceMassFlux: ${\dot{m}}^{"}$ in Eqn. (2115).
BoundaryHeatFlux<Liquid Phase Name>: ${q ″}_{w l}$ in Eqn. (2119).
BoundaryHeatFlux: ${q ″}_{w l g}$ in Eqn. (2120).
BoundaryHeatFlux<Vapor Phase Name>: ${q ″}_{w g}$ in Eqn. (2121).
InterphaseMassTransferRate: The mass transfer between phases due to a single reversible process, such as Bulk Boiling or Species Dissolution. This value is positive when the mass transfer is towards the first phase in the interaction. For continuous-disperse interactions, the first phase is the continuous phase. If the continuous phase is the liquid phase in a boiling problem, a positive rate signifies condensation and a negative rate signifies evaporation.