谐波平衡
某些非稳态流体具有定期重复的流体模式,即它们具有时间周期性。 考虑从风扇叶片流经管道入口的流体。 管道中瞬时流体的测量将显示定期重复模式。 如果流体干扰足够大,并且传播到管道末端,则管道中任何点处的非稳态流体的测量会显示重复模式。 可以使用傅立叶级数表示此类时间周期性模式。
傅立叶级数是共同重现周期函数的正弦和余弦项的级数。
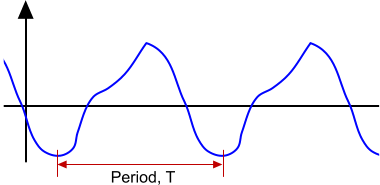
此周期函数(也称为三角级数)的简写形式为:
Simcenter STAR-CCM+ 谐波平衡方法是用于计算流体动力学的混合频率/时间域方法。 使用该方法,可以高效计算时间周期性流体。 非稳态求解存储在少量固定时间级别上(求解快照),存储时间长度为每个叶片排的单一叶片气道中非稳态流体的一个时间段;因此,求解在构造上具有周期性。 单个时间级别会通过表示纳维-斯托克斯方程中时间导数项的频谱运算符耦合到另一时间级别,以及通过周期性和非反射边界条件的应用在计算域的边界处进行耦合。
应用
使用谐波平衡方法,可以快速计算具有时间周期性的非稳态流体求解。 因此,此方法可用于各种应用,包括:
- 涡轮机
- 声调气动声学
- 颤振和受迫响应
- 旋翼飞机
除了快速计算周期性非稳态求解,谐波平衡方法还可以考虑叶片间相位角效应。 此额外优势意味着谐波平衡方法非常适合于涡轮机模拟。 使用谐波平衡方法,可以表示当仅网格化给定轮机排中的一个叶片时,求解如何随该涡轮机排中叶片的不同而变化。 仅网格化每个排中的一个叶片可以极大降低计算成本。
优势
谐波平衡方法的主要优势是可以使用稳态流体求解器方法求解非稳态流体问题。 这意味着,该方法通常比传统的准时时间行进方法更快。
局限
该方法用于处理临时周期性流体,甚至一些“接近”周期性流体。 它不适合非时间周期性的瞬态问题。
目前,K-Epsilon、K-Omega 和 Spalart-Allmaras 湍流模型均可用于谐波平衡。 但是,这些湍流模型的设置和使用与传统非稳态计算中的方式相同。
多孔挡板、风扇和充分发展的交界面不适用于谐波平衡。
在 Simcenter STAR-CCM+ 中使用谐波平衡方法
以下章节提供有关 Simcenter STAR-CCM+ 中谐波平衡方法的信息。