Electrochemical Surface Reactions (Heterogeneous)
Electrochemical surface reactions either produce electrons (anodic) or consume electrons (cathodic). Any number of these reactions can occur at any given time at the interface between a metal and an electrolyte.
A general form of electrochemical surface reactions is represented as:
where is the surface overpotential.
where is the stoichiometric coefficient of the reaction component, is the stoichiometric coefficient of the electron, and is Faraday's constant.
where is the phase interaction area density in dimension 1/Length.
where represents the potential of the conductor, represents the potential of the electrolyte relative to a reference electrode, is the equilibrium potential, is the boundary-specific electric current, and is the resistance that is specified at the boundary or interface.
is generally obtained from the Electrodynamic Potential model. For electrochemically reacting boundaries, is specified in the physics values at each boundary, whereas it is also determined from the Electrodynamic Potential model in the case of an interface or a region when the porous media model is used.
where is the electric potential.
The driving force behind these reactions is the difference in Gibbs free energy between the reactants and the products—which equates to the equilibrium potential . For the electrochemical reaction:
The potential difference at the interface is due to the difference in potential of the metal and the electrolyte.
In Simcenter STAR-CCM+, the potential difference is defined as:
where is the potential of the conductor and is the potential of the electrolyte.
The overpotential definition is equivalent to that of the overpotential which is defined for the electrodynamic potential model in Eqn. (4295) where:
-
is equivalent to
This value represents the potential of the boundary on the conductor region side of the interface which corresponds to the second boundary that you select when defining an interface.
-
is equivalent to
This value represents the potential of the boundary on the electrolyte region side of the interface which corresponds to the first boundary that you select when defining an interface.
- represents the equilibrium potential .
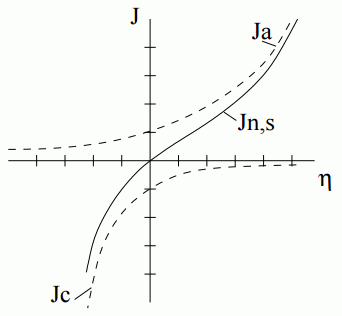
If the potential difference at the interface is larger than the equilibrium potential, , the reaction is anodic. If the potential difference is less than the equilibrium potential, , the reaction is cathodic. When the equilibrium potential is zero, the anodic and cathodic reactions balance, and the net flux is zero.
Anodic reactions (that produce electrons) are related to positive overpotential. Cathodic reactions (that consume electrons) are related to negative overpotential. In these reactions, the current density is positive for anodic reactions and negative for cathodic reactions.
The flow of charged particles determines the current (electrons in the metal and ions in the electrolyte).
- Butler-Volmer
- Tabular
- Tafel
- Tafel Slope (log 10)
- Transport Limited Tafel Slope (log 10)
In each of these reaction formulation property methods, temperature is essential to parameterize the rates of electrochemical reactions. In particular, temperature influences the equilibrium potential when it is specified using the Nernst Equilibrium Potential method. When either the gas, liquid, multicomponent gas, or multicomponent liquid model is selected, the temperature is determined by the energy models that are selected. If no energy model is selected, Simcenter STAR-CCM+ uses a constant temperature of 293.15K. However, when one of the Multiphase models is selected, the temperature is calculated as follows:
- When the Mixture Multiphase (MMP) model or Volume of Fluid (VOF) model is selected, the default energy models calculate one temperature for the combined mixture of phases.
- When the Eulerian Multiphase (EMP) model is
selected, you can select the Phase Coupled Energy model—this energy model
solves for temperature in each phase. The Electrochemical Reactions model
then calculates a weighted average temperature
: (4127)where for each phase, :
- is the volume fraction.
- is the density.
- is the heat capacity.
- Butler-Volmer
- When a reaction is reversible, both anodic and cathodic Tafel equations are combined to form the Butler-Volmer equation:
- Tabular
- The Tabular Polarization Curve method allows you to simulate electrochemical reactions using tabular data that defines the current and electrochemical potential at the interface between the metal and the electrolyte. The Tabular method lets you import polarization curves when modeling species that do not follow the same pattern as generalized by the Butler-Volmer equation.
- Tafel
- Butler-Volmer kinetics accounts for both
anodic reactions in which free electrons are produced in the solid phase,
and cathodic reactions in which free electrons are consumed. In some
scenarios, if one of the apparent transfer coefficients is small or operates
solely in either positive or negative surface overpotential conditions,
reactions can exhibit currents in only anodic or cathodic directions. In
such cases, either
or
is neglected and the negligible reaction
term is disregarded. The specific reaction current
then reads: (4132)
- Tafel Slope (log 10)
- The Tafel equation is often laid out and
parameterized as it is in the Butler-Volmer section, with both exponent
variables independent of electric potential. In practice, often these
exponent variables are measured as one combined quantity,
, and called the Tafel Slope:
(4133)so the specific reaction current is expressed as:(4134)
- Transport Limited Tafel Slope (log 10)
- The Transport Limited Tafel Slope method
approximates effects that are not initially accounted for in the simulation
setup. When a positive limiting current
is specified, the specific reaction current
that is provided by the Tafel method (Eqn. (4132)) is limited: (4136)This method of modeling is empirical and is not based on first principles.
Double Layer Capacitance
The reaction formulation methods calculate the faradaic electric current density that result from electrochemical reactions. As a consequence of ion and electron attraction or repulsion, electric charges accumulate on the reaction site between the electrode and electrolyte, causing transient (non faradaic) capacitive electric currents. The impact of this phenomenon is modeled with a double layer capacitor that is connected in parallel to the main electrochemical reaction site. In transient mode, this configuration creates an additional double layer capacitance electric current density over the electrochemical reaction site.
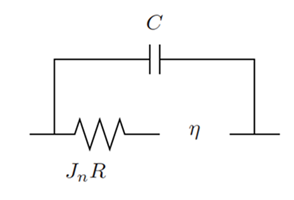
- at a constant time-step.
- at a constant time-step.
- is the double layer capacitance.
- denotes the current time-step.
Nernst Equilibrium Potential
When the equilibrium potential is specified using the Nernst Equilibrium Potential method, is computed as:
is the Nernst Standard Potential at the reference molar concentration of unity.
Nernst Equilibrium Potential from Thermodynamic Data
When the equilibrium potential is specified using the Nernst Equilibrium Potential from Thermodynamic Data method, is computed as:
in which is temperature, is the stoichiometric coefficient of electrons, and is the stoichiometric coefficient of reactant species . and is positive for species/electrons that are reactants, and negative for species/electrons that are products. has a value of 1, except at interfaces when ionic species reside on the solid side of the interface, then has a value of -1.
- For liquids, the activity is the molar fraction .
- For gases, the activity is , where is the species mole fraction, is the absolute pressure, and is the reference pressure ([1.0 atm]).
- For electrochemical species, the activity is
- For sub-grid particle intercalation species, the activity is:
(4142)where is the surface molar concentration, is the maximum molar concentration, and is the vacancy rate exponent.
Electrochemical Reaction Heating
The Electrochemical Reaction Heating model accounts for heat contributions which are due to reversible and irreversible electrochemical processes (for heat contributions due to sorption, see Eqn. (4174)). This feature is important for applications such as electroplating or solid oxide fuel cells which create high electrochemical currents.
Simcenter STAR-CCM+ calculates the heat contributions that are released from the reacting surface interface according to:where, for the Butler-Volmer method, the irreversible heat contribution is always positive:
represents the boundary specific electric current density on the solid for species , is the surface overpotential for species , and represents the reversible heat contribution.
On contact interfaces, the contribution to the cell center source term of the energy equation is weighted by the effective thermal conductivities of the neighboring physics continua.| 注 | If the Tafel method is selected and operates at negative overpotentials that are outside the valid range of approximation, it is possible that negative irreversible heat release rates are predicted as a consequence. |
For Eulerian multiphase, the specific electrochemical reaction heat surface source term contributions from each phase is expressed as:
where is the volume fraction of phase for each side of the interface/boundary, and is the specific reaction current that is provided by the Butler-Volmer method, Eqn. (4129).