电镀层

可使用 Simcenter STAR-CCM+ 中的电镀层模型来模拟电涂层，并确定沉浸在涂料液体中的指定表面上的涂料层厚度。

需要根据给定的工艺参数对特定的涂料液体进行校准。该模型可与 VOF 多相模型组合使用，以覆盖浸入涂料池的体产生的气泡。下图说明了模型公式中使用的符号。

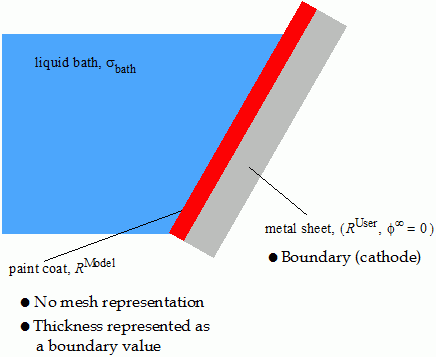
该公式进行如下假设：

Simcenter STAR-CCM+ 使用涂层表面（边界）处的可用函数对涂料层相进行建模，而非以体网格进行表示。
该公式假设电势处于准稳态。将同时求解稳态方程和可能的时间相关边界条件。
将根据实际工艺参数校准模型。
电势场和层增长不会影响流场。

基本传输方程指具有零源项的电势方程 (Eqn. (4277)) 加上边界条件 Eqn. (4279)。在这里，

σ

为液池的导电率。在阳极处，为

\bar{ϕ}

应用可能随时间变化的值。在有涂层的阴极处，设置与金属板的厚度及其导电率呈函数关系的用户自定义电阻。用户自定义电阻会影响 Eqn. (4279) 中的

R^{ex}

。金属板中心的电势假设为零。电镀层模型计算涂料层电阻，该电阻也会影响 Eqn. (4279) 中的

R^{ex}

，如下所示：

使用微分方程计算涂料层电阻时，可使用以下起始方程：
图 1. EQUATION_DISPLAY

$\frac{d R_{p a int}}{d t} = \frac{d h}{d t} r_{paint} + g$

(4179)
指定用于计算涂料层电阻的涂料层电阻率时：
图 2. EQUATION_DISPLAY

$R_{p a int} = r_{p a int} \times h$
(4180)
直接指定涂料层电阻时：
图 3. EQUATION_DISPLAY

$R_{p a int} = R_{paint}^{user}$
(4181)

在这里， $h$ 为涂料层厚度（单位： $[m]$ ）。默认情况下，偏移标量分布 $g$ 为零。涂料层电阻率为 $r_{paint}$ ，涂料层总电阻为 $R_{paint}$ 。

涂料层增长率（涂料沉积率）是涂料池和涂料表面之间交界面处的边界单位电流 $j_{n}$ 的函数。沿涂层体边界的涂料层厚度的 ODE（常微分方程）如下所示：

图 4. EQUATION_DISPLAY

\frac{d h}{d t} = \frac{c_{paint}}{ρ_{paint}} (j_{n} - j_{m i n})

(4182)

其中， $j_{n}$ 通过边界条件进行计算。比例因子为以下电化学当量 $E$ 的倒数：

图 5. EQUATION_DISPLAY

E = \frac{ρ_{paint}}{c_{paint}}

(4183)

$ρ_{paint}$ 为涂料固体的密度（单位： $[k g / m^{3}]$ ）， $c_{paint}$ 为固体涂料库仑效率（单位： $[k g / C]$ ）。 $j_{m i n}$ 为确保边界处出现任何沉积所需的最小单位电流 ( $[A / m^{2}]$ )。该公式假设沉积率始终大于等于零。

不同涂料混合物的极化效应测量结果指明，存在可控制涂料层增长的先进机制。将对非线性函数进行积分，然后可使用最小累积单位表面电荷或最小单位电流平方时间积分标量分布控制对厚度增加的影响。基于各个涂料标定且大于 0 的值会影响模拟得到的涂料层厚度分布。