ReTheta_t 相关性

$R{e}_{\theta t}$ 既定的相关性由 Abu-Ghannam 和 Shaw [374] 提出。

在零压力梯度情况下，此相关性为：

其中，$Tu$ 为湍流强度。

由 Menter 等人 ([380]) 针对 Gamma ReTheta 转换模型提出的替换表达式为：

此表达式后经 Langtry [378] 修订，旨在改进较低自由流湍流强度时的结果，如下所示：

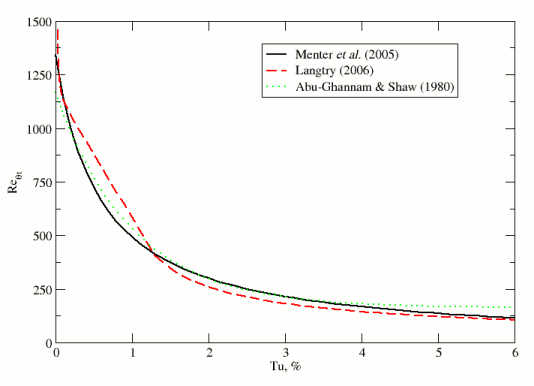
下图中已绘制三种零压力梯度相关性。Simcenter STAR-CCM+ 中提供了所有这三种相关性，使用户能够灵活地自定义相关性，但Eqn. (1530) 是内部 "Suluksna-Juntasaro" 校准中默认使用的相关性。

${\mathrm{Re}}_{\theta t}$ vs. 自由流湍流强度

对于 Eqn. (1528) 至 Eqn. (1530) 中为零压力梯度呈现的三种相关性，最初均以包含压力梯度效应的形式呈现。有一点疑问：${\mathrm{Re}}_{\theta t}$ 相关性[385] 中需要压力梯度效应，因为它们可以引入压力梯度效应的双重计算。但是，它们以可选方式包括在 Simcenter STAR-CCM+ 中。如果存在压力梯度，相关性需要计算 Thwaites 参数 ${\lambda }_{\theta }$，而在由 Menter 等人 [380] 提出的相关性中，需要计算加速度参数 $K$。

Thwaite 参数 ${\lambda }_{\theta }$ 定义为：

其中：

参数 $K$ 定义为：

$s$ 表示壁面平行方向，其中使用流向和壁面法向构造局部坐标系。

湍流强度从湍动能中得出，如下所示：

流向速度梯度计算方法如下：

其中，${\overline{\mathbf{\text{v}}}}^T$ 表示 $\overline{v}$ 的转置。

由于动量厚度 $\theta$ 必须从动量厚度雷诺数 ${\mathrm{Re}}_{\theta }$ 中衍生得出，因此相关性将成为迭代求解的隐式函数。

Abu-Ghannam 和 Shaw [374] 提出的非零压力梯度 (NZPG) 相关性为：

其中：

为了确保数值稳定性，将应用以下限制：

Menter 等人 ([380]) 提出的 NZPG 相关性为：

其中：

为了确保数值稳定性，将应用以下限制：

Langtry[378]提出的 NZPG 相关性为：

为了确保数值稳定性，将应用以下限制：

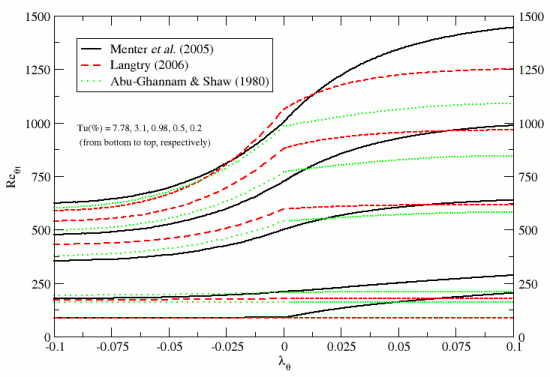
下图对比显示了一系列自由流湍流强度的三种 NZPG 相关性。

${\mathrm{Re}}_{\theta t}$ vs. ${\lambda }_{\theta }$ 用于各种自由流湍流强度值