Windows
The problem of discontinuities at the edge can be alleviated either by ensuring that the signal and the sampling period are synchronous or by ensuring that the function is zero at the start and end of the sampling period. This latter situation can be achieved by applying what is called a 'window function' which normally takes the form of an amplitude-modulated sine wave.
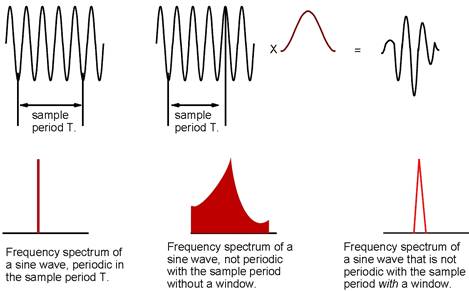
The use of windows gives rise to errors itself, of which the user should be aware and which should be avoided if possible. The various types of windowing functions distribute the energy in different ways. The choice of window depends on the input function and on your area of interest.
Self-Windowing Functions
Self-windowing functions are those that are periodic in the sample period T or transient signals. Transient signals are those where the function is naturally zero at the start and end of the sampling period such as impulse and burst signals. Self-windowing functions should be adopted whenever possible since the application of a window function presents problems of its own. A rectangular or uniform window can then be used since it does not affect the energy distribution.
| 注 | It should be noted that synchronizing the signal and the sampling time, or using a self-windowing function is preferable to using a window. |
Window Characteristics
The time windows provided take a number of forms—many of which are amplitude-modulated sine waves. These are all, in effect, filters, and the properties of the various windows can be compared by examining their filter characteristics in the frequency domain, where they can be characterized by the factors shown below.
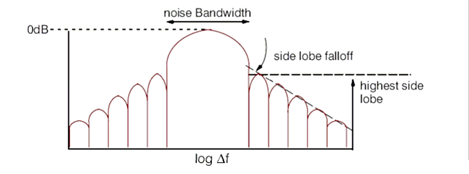
The windows vary in the amount of energy squeezed in to the central lobe as compared to that in the side lobes. The choice of window depends on both the aim of the analysis and the type of signal you are using. In general, the broader the noise bandwidth, the worse the frequency resolution, since it becomes more difficult to pick out adjacent frequencies with similar amplitudes. On the other hand, selectivity (i.e. the ability to pick out a small component next to a large one) is improved with side lobe falloff. It is typical that a window that scores well on bandwidth is weak on side lobe falloff and the choice is therefore a tradeoff between the two. A summary of these characteristics of the windows provided is given in table 1-1.
| Window type | Highest side lobe
(dB) |
Side lobe falloff
(dB/decade) |
Noise Bandwidth
(bins) |
Max. Amp error (dB) |
|---|---|---|---|---|
| Hanning
(or Hann) |
-32 | -60 | 1.5 | 1.4 |
| Hamming | -43 | -20 | 1.36 | 1.8 |
| Blackman | -92 | -20 | 2.0 | 1.1 |
| Bartlett | -26 | -38 | 1.34 | — |
Window Types
The following windows—Hanning, Hamming, Blackman, and Bartlett—all take the form of an amplitude-modulated sine wave in the time domain. For a comparison of their frequency domain filter characteristics, see table 1-1.
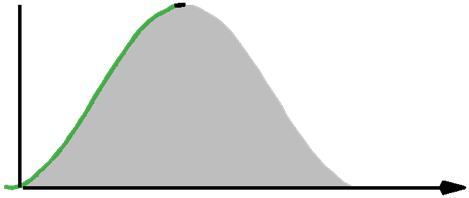
- Hanning (or Hann)
- This window is most commonly applied for general-purpose analysis of random signals with discrete frequency components. It has the effect of applying a round-topped filter. The ability to distinguish between adjacent frequencies of similar amplitude is low, so it is not suitable for accurate measurements of small signals.
- Hamming
- This window has a higher side lobe than the Hanning but a lower fall-off rate and is best used when the dynamic range is about 50 dB.
- Blackman
- This window is useful for detecting a weak component in the presence of a strong one.
- Bartlett
- This window is a triangular type. It is similar to a rectangular window but has smoother transitions between zero and one.