Defining Linear Elastic Materials

Linear elastic materials deform elastically under loading, returning to their original shape when the load is removed. In general, you can use a linear elastic description for modeling most metals, provided that the stress on the material is below the yield stress.

Linear elastic materials obey Hooke's law, which defines a linear stress-strain relationship. For more information, see Linear Elastic Materials.

By default, Simcenter STAR-CCM+ treats the solid materials as compressible. Linear elastic materials are considered incompressible when their Poisson's ratio $ν \to 0.5$ . If, in any direction, $ν > 0.45$ , activate the Nearly Incompressible Material model in the solid stress physics continuum.

The Linear Elasticity model cannot be used if you have selected both the Nearly Incompressible Material and Nonlinear Geometry models in the solid physics continuum. In this case, select the Hyperelasticity model.

To define a linear elastic material:

Create a material law and assign it to the relevant solid materials, as explained in Defining the Solid Materials.
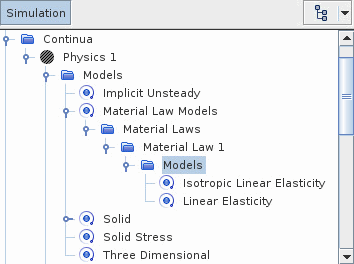
Right-click the Material Laws > [Material Law 1] > Models node and choose Select models...

In the Material Law 1 Model Selection dialog, activate the following models:


Group box	Model
Material Stiffness Models	Linear Elasticity
Material Strain Measures	To model linear geometries, activate Linear Strain (Small Strain). To model nonlinear geometries, activate Green-Lagrange (Small Strain).
Linear Elastic Material Models	To model materials that have the same mechanical properties in all directions, activate Isotropic Linear Elastic. To model materials that have independent mechanical properties along three mutually-orthogonal directions, activate Orthotropic Linear Elastic. To model materials that have independent mechanical properties in all directions, activate Anisotropic Linear Elastic.

For more information, see Linear Elastic Materials.

Simcenter STAR-CCM+ adds the relevant material properties under the Material Properties node, based on the specified linear elastic material model:

For orthotropic or anisotropic material laws, you define the material properties of each solid region with respect to a local coordinate system:

For each region, select the Regions > [region] > Physics Values > Material Law Orientation node and set Orientation to the appropriate coordinate system. For more information, see Orientation Manager and Local Orientations.
You can visualize the material coordinate system in a scene using the basis vector field functions. See Local Material Coordinate System.

This step is not required for isotropic materials, as their properties are the same in all directions.

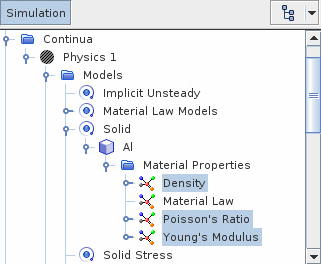
Define the material properties as required. For each material:

Expand the Material Properties node.
Specify the material Density.

Specify the remaining properties based on the selected linear elastic material model:


Linear Elastic Material Model	Steps
Isotropic Linear Elastic	Specify the Poisson's Ratio and Young's Modulus. See Eqn. (4513).
Orthotropic Linear Elastic	Specify the Poisson ratio, shear modulus, and Young's modulus along each axis of the specified coordinate system (see Eqn. (4506)): Expand the Poisson Ratios > Poisson Coefficients node and specify the three coefficients nu12, nu23, and nu13. Expand the Shear Moduli > Shear Modulus Coefficients node and define the three coefficients G12, G23, and G13. Expand the Young's Moduli > Young's Modulus Coefficients node and define the three coefficients E12, E23, and E13.
Anisotropic Linear Elastic	Expand the Anisotropic Stiffness Coefficients > Anisotropic Material Stiffness Tangent Coefficients node and specify the independent components of the material tangent matrix. See Eqn. (4504).

If required, continue by defining any thermal properties. See Defining Thermal Properties.
For more information, see Material Properties.
Optionally, you can account for plastic yield. For instructions, see Defining Elastoplastic Materials.