变形

区域边界的位置和形状可以随时间变化，例如由于接触体的运动。在 Simcenter STAR-CCM+ 中，变形算法根据边界位移重新分布网格节点，使网格可以进行非刚性变形。

变形算法将重新分布网格节点，它对网格单元体积、面或边不起作用。变形无法计算网格质量度量，因此不会优化网格。

通过一组控制点定义变形施加在网格上的初始移动。这些控制点源自变形边界上的网格节点或源自控制点表。每个控制点与一个已知的位移矢量关联。变形使用这些位移构建插值场，用于计算所有网格节点的位移。

变形使用控制点位移为区域生成一个插值场，用于定义变形运动。然后，变形使用该插值场将网格节点平移到新位置。

插值算法

Simcenter STAR-CCM+ 提供了 BSpline 和径向基函数 (RBF) 这两种插值法。 BSpline 系数和并行化格式仅限局部，因此 BSpline 变形对并行计算而言比 RBF 更具可扩展性，可能会减少计算开销。

BSpline

根据 [18]，Simcenter STAR-CCM+ 根据渐进自适应网格使用多级 BSpline 层级方法。

插值法为 C² 连续曲线，该方法生成的表面比 C⁰ 或 C¹ 连续曲线更平滑。

考虑一个简单的 1D 示例。下图显示了一条线段，“节点”处有 4 个 BSpline 系数（标记为 0-3），沿该线段等距间隔。参数 $s$ 是可能包含一个或多个控制点的间隔内的标准化距离：

在此示例中，BSpline 曲线通过控制点（未显示）沿叠加到几何域的一条线拟合。根据定义，这些点不与模型几何重合，而是围绕网格节点。中心间隔 (1)-(2) 内的三次 BSpline 曲线至少需要 4 个系数：

图 1. EQUATION_DISPLAY

f (x) = \sum_{k = 0}^{3} B_{k} (s) ϕ_{k}

(4845)

其中：

$f (x)$ 为拟合曲线。
$s$ 为沿间隔的标准化距离
$ϕ_{k}$ 为节点 $k$ 处的 BSpline 系数值，且 $k$ =0、1、2 和 3。

权重函数

B_{k} (s)

是均匀基函数，由以下公式给出：

图 2. EQUATION_DISPLAY

\begin{matrix} B_{0} (s) = {(1 - s)}^{3} / 6 \\ B_{1} (s) = (3 s^{3} - 6 s^{2} + 4) / 6 \\ B_{2} (s) = (- 3 s^{3} + 3 s^{2} + 3 s + 1) / 6 \\ B_{3} (s) = s^{3} / 6 \end{matrix}

(4846)

这些函数充当加权因子。每个函数都对 $ϕ_{k}$ 具有适当的影响，使得 $\sum_{k = 0}^{3} B_{k} = 1$ 。

该方法可轻松扩展到 2D 和 3D 情况：

图 3. EQUATION_DISPLAY

\begin{matrix} f (x, y) = \sum_{k = 0}^{3} \sum_{l = 0}^{3} B_{k} (s) B_{l} (t) ϕ_{k l} \\ f (x, y, z) = \sum_{k = 0}^{3} \sum_{l = 0}^{3} \sum_{m = 0}^{3} B_{k} (s) B_{l} (t) B_{m} (v) ϕ_{k l m} \end{matrix}

(4847)

其中， $B_{k} (s)$ 、 $B_{l} (t)$ 和 $B_{m} (v)$ 分别为 $x 、 y$ 和 $z$ 坐标方向上的基函数；这些函数描述了 1D 直线、2D 正方形或 3D 立方体上的节点（如适用）。

Simcenter STAR-CCM+ 中实现的 BSpline 方法采用层级过程，即：逐渐加密控制点网格，直到残差在变形容差指定的限制范围内。按不同的网格尺度应用一系列校正。为简单起见，将坐标命名为 $x_{i}$ ，其中 $i = 1, 2, ... n$ 表示网格加密时间步， $t$ 表示目标坐标，残差即这些坐标之差， $r_{i} = t - x_{i}$ 。残差实际上是位移，这在控制点处已知，但在其他位置则未知。

在达到所需的位移之前，残差可以表示为插值 $I_{i}$ 与剩余残差 $r_{i - 1} = I_{i} + r_{i}$ 之和。

$t$ 方程如下所示：

图 4. EQUATION_DISPLAY

t = x_{0} + \sum_{i = 1}^{n} I_{i} + r_{n}

(4848)

其中， $x_{0}$ 为该过程开始时点的坐标， $I_{i}$ 为时间步 $i$ 处的插值， $n$ 为最后一个加密时间步，在该时间步将达到所需的位移。

执行加密，直到变形误差收敛到变形容差的精度范围内。由于接近数据集越来越小，在特定加密等级，每个数据集仅包含一个控制点并实现精确插值，因而可保证此类算法的收敛。

层级方法效率低下，因为计算点数会随着加密呈指数增长，而许多计算针对的区域中没有数据。更有效的方法是从计算中移除这些点。根据 Eqn. (4848)，仅当符合下列任一条件时，系数 $ϕ$ 才会等于零：

来自接近数据点的所有贡献为零，或
接近数据集为空。

在这两种情况下，可以假设这些点处的样条曲线校正已收敛，不需要进一步校正。因此，在后续的加密等级，该算法仅收集非零系数，该过程名为自适应插值。加密后，控制栅格中的点数会增加，但是相反，需要校正的点将减少。

下图显示了加密等级 0 处的控制栅格（左图）和级别 n 处的加密控制栅格（右图）：

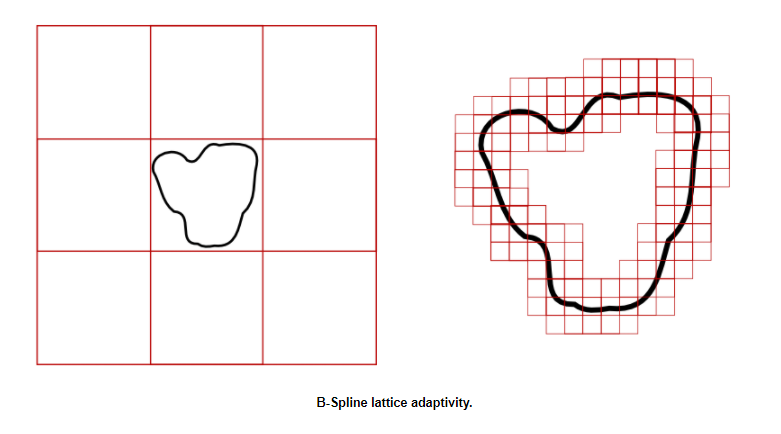
如果在边界表面（黑线）上定义了控制数据点，在特定加密等级后，不会校正内部区域节点。操作数为 $O (M + N) \times n$ 阶，其中 $M$ 为控制点数（即，存在位移的节点）， $N$ 为计算点数（即，几何中的所有节点）， $n$ 为加密等级数。

径向基函数 (RBF)

RBF 变形通过一个方程组生成插值场；可使用控制点及其指定的位移创建这些方程，其中每个控制节点 $i$ 的已知位移 ${d'}_{i}$ 展开为

图 5. EQUATION_DISPLAY

{d'}_{i} = \sum_{j = 1}^{N} f_{b, j} (r_{i j}) λ_{j} + α

(4849)

其中， $f_{b, j} (r_{i j})$ 是形状的径向基本函数

图 6. EQUATION_DISPLAY

f_{b, j} (r_{i j}) = \sqrt{{r_{i j}}^{2} + {c_{j}}^{2}}

(4850)

$r_{i j}$ 是两个节点之间的距离的幅值：

图 7. EQUATION_DISPLAY

r_{i j} = | x_{i} - x_{j} |

(4851)

在这些方程中， $λ_{j}$ 是展开系数， $x_{i}$ 是节点 $i$ 的位置，N 是控制节点的数量， $c_{j}$ 是基本常数。在 Simcenter STAR-CCM+ 中，基本常数设为零。常数矢量 $α$ 用于满足额外约束

图 8. EQUATION_DISPLAY

\sum_{j = 1}^{N} λ_{j} = 0

(4852)

此额外约束限制大 $x$ 的展开。如果对于所有 $i \neq j$ ， $x_{i} \neq x_{j}$ ，则 Eqn. (4849) 中所述的系统非奇异。

方程 Eqn. (4849) 和 Eqn. (4852) 求解后，得出所有 $λ_{j}$ 的笛卡尔分量和常数矢量 $α$ 的分量。这会产生所需的插值场：

图 9. EQUATION_DISPLAY

d' (x) = \sum_{j = 1}^{N} f_{b, j} (r) λ_{j} + α

(4853)

其中， $f_{b, j} (r)$ 应用于网格中的所有节点，即

\begin{matrix} f_{b, j} (r) = \sqrt{r^{2} + {c_{j}}^{2}} \\ r = | x- x_{j} | \end{matrix}

此方程现在可用于按计算出的位移 $d'$ 移动网格节点。

方程 Eqn. (4849) 和 Eqn. (4853) 中所涉及的矩阵是密集矩阵，简单矩阵运算需要 $O (N^{2})$ 运算。已开发出 $O (N \log (N))$ 方法，可在许多节点位置求解线性方程 Eqn. (4849) 和计算方程 Eqn. (4853)。 RBF 变形使用具有特殊预调节器（[15]、[16]）的共轭梯度法以及快速多极法 [17] 加速矩阵矢量乘法的计算。

边界平面条件（RBF 变形）

Simcenter STAR-CCM+ 为变形边界上的节点提供两个约束：边界平面和固定边界平面约束。对于固定边界平面条件，位于指定平面上的节点固定；而对于边界平面条件，允许这些节点在平面自身内移动。通过使用控制节点，可以实现类似于固定边界平面条件的作用，但固定边界平面条件本身效率更高。约束平面附近节点的移动因此与平面上节点的移动顺利结合起来。

可以使用如下所述的阻尼距离 $L_{p}$ 控制约束平面附近的这一移动，但这仅适用于 RBF 变形。

在求解 Eqn. (4849) 之前施加这些约束。在准备时，通过求解以下方程，用户指定的位移 $d_{i}$ 转换为 ${d'}_{i}$

图 10. EQUATION_DISPLAY

d_{i} = \prod_{p = 1}^{N_{p}} [s_{p} n_{p} n_{p}^{T} + t_{p} (1 - n_{p} n_{p}^{T})] {d'}_{i}

(4854)

其中， $n_{p}$ 是第 p 个平面的法线， $N_{p}$ 是平面的数量。在变形过程结束时，位移 ${d'}_{i}$ 与其他网格节点一起转换回 $d_{i}$ 。 $s_{p}$ 和 $t_{p}$ 是与选定平面类型和连续性条件相关的函数。这些函数如下所示：


	$C^{0}$ 连续		$C^{2}$ 连续
	$s_{p}$	$t_{p}$	$s_{p}$	$t_{p}$
固定边界平面	$f_{0} (l)$	$f_{0} (l)$	$f_{2} (l)$	$f_{2} (l)$
边界平面	$f_{0} (l)$	1	$f_{2} (l)$	1

此处：

图 11. EQUATION_DISPLAY

f_{0} (l) = {\begin{matrix} 1 \\ 1 - {(1 - l)}^{3} \\ 0 \end{matrix} \begin{matrix} ; l \geq 1 \\ ; 1 > l \geq 0 \\ ; l < 0 \end{matrix}

(4855)

图 12. EQUATION_DISPLAY

f_{2} (l) = {\begin{matrix} 1 \\ l^{3} & (10 - 15 l + 6 l^{2}) \\ 0 \end{matrix} \begin{matrix} ; l \geq 1 \\ ; 1 > l \geq 0 \\ ; l < 0 \end{matrix}

(4856)

其中

图 13. EQUATION_DISPLAY

l = \frac{n_{p} (x - x_{0, p})}{L_{p}}

(4857)

是第 p 个平面到 $x_{i}$ 的有符号距离与阻尼距离 $L_{p}$ 之比。 $x_{0, p}$ 是第 p 个平面上的位置矢量， $L_{p}$ 输入为有限距离，或自动计算为 $(L_{m i n} + L_{m a x}) / 2$ 。 $L_{m i n}$ 和 $L_{m a x}$ 分别是平面到位于平面活动侧的最近和最远控制节点的距离。

下面绘制了函数 $f_{0}$ 和 $f_{2}$ 在范围 0 到 1 内的变化以进行比较。连续性等级 $C^{2}$ 产生平滑过渡。

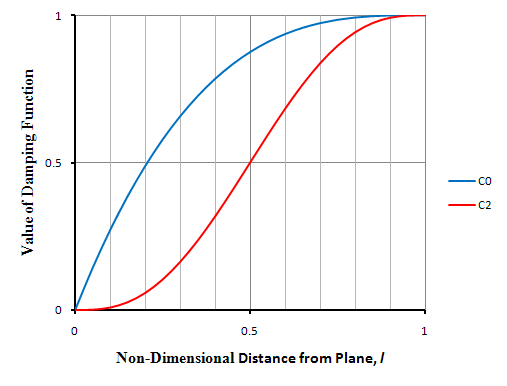
时间步中 RBF 变形阶段所包含的步骤如下：

控制节点位移 $d_{i}$ 根据 Eqn. (4854) 转换为 ${d'}_{i}$ 。
Eqn. (4849) 通过 Eqn. (4852) 求解，以提供插值场。
利用 Eqn. (4854)，位移矢量从 ${d'}_{i}$ 转换为 $d_{i}$ 。

线性拟合

线性拟合可与 BSpline 和 RBF 变形一起使用。

每个位移分量 $(d x, d y, d z)$ 表示为坐标的函数。使用最小二乘法，得出每个位移分量的超平面方程。

考虑 x 位移 $d x$ 的拟合问题：

$d x (x, y, z) = A x + B y + C z + D$

可以构造超定线性方程组

$(\begin{matrix} ⋮ & ⋮ & ⋮ & ⋮ \\ x_{i} & y_{i} & z_{i} & 1 \\ ⋮ & ⋮ & ⋮ & ⋮ \\ ⋮ & ⋮ & ⋮ & ⋮ \end{matrix}) (\begin{matrix} A \\ B \\ C \\ D \end{matrix}) = (\begin{matrix} ⋮ \\ {d x}_{i} \\ ⋮ \\ ⋮ \end{matrix})$

矩阵形式为

$P c = d x$

其中， $P$ 为带点坐标的矩阵， $c$ 包含超平面系数， $d x$ 为位移列。

要使用最小二乘法解决此问题，需构造正规方程：

$c = P^{+} d x$ ，其中 $P^{+}$ 为伪逆矩阵。

RBF 变形使用 Cholesky 分解来求解线性方程。对于 BSpline 线性拟合实现，使用奇异值分解 (SVD) 方法分解该矩阵。