坐标系

在 Simcenter STAR-CCM+ 中，可以指定相对于笛卡尔坐标系和曲线坐标系的矢量和张量物理量。曲线坐标系相对于参考笛卡尔坐标系进行定义。

笛卡尔坐标系

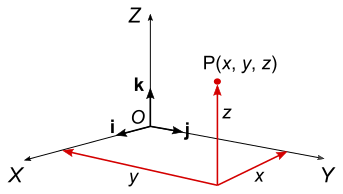
笛卡尔坐标系由三个在原点处汇合的右旋相互正交轴（通常标记为 X、Y 和 Z）来定义。点的位置由其沿坐标系轴的 x、y 和 z 坐标给定。矢量相对于与 X、Y 和 Z 轴对齐的单位基矢量（请参见 Eqn. (5185)）进行描述。定义笛卡尔坐标系的单位基矢量通常标记为 i、j 和 k。

对于圆柱对称的物理域（例如绕轴旋转不变的坐标系），可以很方便地相对于圆柱坐标系来定义物理量。在圆柱坐标系中，点的位置由其径向、切向和轴向坐标

r

、

θ

和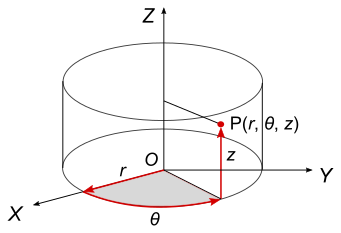

z

给定：

圆柱坐标系相对于参考笛卡尔坐标系（可以是基准坐标系或局部笛卡尔坐标系）进行定义。如果 $(x_{R}, y_{R}, z_{R})$ 是点在参考笛卡尔坐标系中的坐标，则点在圆柱坐标系中的坐标为：

图 1. EQUATION_DISPLAY

\begin{array}{l} r = \sqrt{x_{R}^{2} + y_{R}^{2}} \\ θ = \tan^{- 1} (\frac{y_{R}}{x_{R}}) \\ z = z_{R} \end{array}

(5222)

矢量和张量相对于与径向、切向和轴向对齐的单位基矢量进行定义。轴向单位矢量相对于参考坐标系固定，而径向和切向单位矢量取决于参考系中的位置。点

(x_{R}, y_{R}, z_{R})

的圆柱单位基矢量为：

图 2. EQUATION_DISPLAY

\begin{array}{l} r = \frac{x_{R} i + y_{R} j}{\sqrt{x_{R}^{2} + y_{R}^{2}}} \\ θ = k \times r \\ z = k \end{array}

(5223)

对于球对称的物理域（例如绕点旋转不变的坐标系），可以很方便地相对于球坐标系来定义物理量。在球坐标系中，点的位置由其径向、极坐标和方位角坐标

r

、

θ

和

ϕ

给定：

球坐标系相对于参考笛卡尔坐标系（可以是基准坐标系或局部笛卡尔坐标系）进行定义。如果

(x_{R}, y_{R}, z_{R})

是点在参考笛卡尔坐标系中的坐标，则点在球坐标系中的坐标为：

图 3. EQUATION_DISPLAY

\begin{array}{l} r = \sqrt{x_{R}^{2} + y_{R}^{2} + z_{R}^{2}} \\ θ = \cos^{- 1} (\frac{z_{R}}{r}) \\ ϕ = \tan^{- 1} (\frac{y_{R}}{x_{R}}) \end{array}

(5224)

矢量和张量相对于与径向、极坐标和方位角方向对齐的单位基矢量进行定义。点

(x_{R}, y_{R}, z_{R})

的球单位基矢量为：

图 4. EQUATION_DISPLAY

\begin{array}{l} r = \frac{x_{R} i + y_{R} j + z_{R} k}{\sqrt{x_{R}^{2} + y_{R}^{2} + z_{R}^{2}}} \\ θ = \frac{k \times r}{‖ k \times r ‖} \\ ϕ = r \times θ \end{array}

(5225)