壁面成核沸腾模型参考

壁面沸腾模型可预测壁面过热量（即壁面温度超过饱和温度的量）以及蒸汽的轴向和径向分布。有关更多信息，请参见沸腾。


理论	请参见壁面沸腾。
提供方式	[相间相互作用]模型选择 > 可选模型
节点路径示例	[相间相互作用] > 模型 > 沸腾/冷凝 > 壁面成核沸腾
要求	激活了对以下模型的欧拉多相模拟：材料：多相、多相流相互作用（自动选择）多相流模型：混合多相 (MMP)（自动激活：多相相互作用、梯度）可选模型：分离多相温度粘滞态：层流或湍流空间：三维、轴对称或二维时间：稳态或隐式非稳态至少有两个欧拉相：一个液相和一个气相。在液相中，以下相模型为激活状态：材料：液体状态方程：恒密度可选模型：壁面距离在气相中，以下模型已激活：材料：气体状态方程：恒密度或理想气体可选模型：壁面距离需要连续-离散拓扑相间相互作用。在相间相互作用中，以下模型为激活状态：可选模型：沸腾/冷凝
属性	关键属性包括：松弛因子。请参见壁面成核沸腾。
激活	物理模型	壁面泡成核请参见壁面泡成核属性。壁面瞬态传导请参见壁面瞬态传导属性。
	模型控制（子节点）	壁面干燥面积分数请参见壁面干燥面积分数属性。
	边界输入	请参见边界设置。
	场函数	请参见场函数。

壁面成核沸腾属性

松弛因子: 调整模型灵敏度。减小该值以改进收敛。

壁面沸腾模型控制

壁面干燥面积分数: 壁面干燥面积分数指定壁面上应用的热通量有多少直接流向蒸汽对流，而不是液体对流和蒸发。它可以用于在收敛求解中提高初始收敛过程中的稳定性，或指示收敛求解中脱离泡核沸腾 (DNB) 条件的开始。
有关详细信息，请参见壁面干燥面积分数。

壁面干燥面积分数属性

方法

基础壁面干燥面积分数

将面积分数定义为零，直到壁面附近的蒸汽体积分数超过指定值。然后在蒸汽体积分数接近 1 时将面积分数转换为 1。

要降低网格依赖性，用于面积分数计算的近壁体积分数可采用最佳方式定义为在近壁指定理论气泡层厚度内求平均值。

此方法是默认设置。

常数、场函数、表和用户程序

针对用户指定值提供的标准方法。

壁面干燥断点

蒸汽体积分数在此点上开始热传递到蒸汽相（请参见 Eqn. (2123)）。默认值为 0.9。

此属性仅适用于基础壁面干燥面积分数方法。

气泡层松弛因子

控制由干燥模型使用的气泡层体积分数的更新。它对于超过干燥标准后的收敛行为有所帮助。默认值为 0.5。

气泡层选项

定义用于对干燥标准中的体积分数求平均值的层厚度。

壁面网格单元
在近壁网格单元中心计算的值表示整个气泡层。这意味着在干燥标准中使用了网格单元中心体积分数。这是默认设置。
固定的直径数
气泡层厚度定义为局部气泡脱离直径乘以此值。
固定的 Yplus
气泡层厚度定义为蒸汽相的壁面湍流长度尺度乘以此值。

壁面泡成核属性

提供以下子节点：

成核密度
气泡脱离直径
气泡脱离频率
升空直径（仅当离散相中选择了自适应多尺寸组 (AMUSIG) 模型或 S-Gamma 模型时）

成核密度属性

成核密度确定受热面上形成气泡的单位面积位置数目。

这是在过冷沸腾机械模型中确定蒸发率的前导因子（请参见 Eqn. (2916)）。下图说明了此参数：

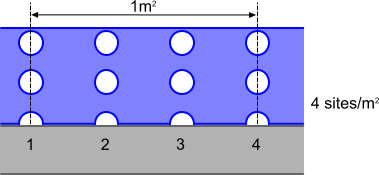
方法

用于计算成核密度的选项。

Lemmert-Chawla
Hibiki-Ishii
用户自定义：常数、场函数、表或用户程序。

Lemmert-Chawla 属性

Lemmert Chawla 模型 ([499]) 与壁面过热相关，并且从稳定性而言建议用于初始研究的默认模型。默认设置假设活动成核点数随壁面过热而变化，幂次为 1.805。此值将在 Tolubinsky 和 Kostanchuk 模型中使用，用于计算气泡脱离直径，例如对 45 bar 的强制对流过冷水沸腾进行建模。

标定常数 A

A

（位于 Eqn. (2128) 中）。根据 Kurul 和 Podowski 的研究 ([494])，选择默认值 1.805。

标定常数 B

B

（位于 Eqn. (2128) 中）。默认值为 0.0。

最大过热

Δ T_{m a x}

（位于 Eqn. (2127) 中）。设置传递至该子模型的壁面过热值的上限，防止在初始收敛过程中溢出。确保此限制不会影响收敛求解中预估的壁面过热值。默认值为 25.0 delta K。

参考成核密度

n_{0}^{"}

（位于 Eqn. (2128) 中）。默认值为 12366.44783/m²。

参考壁面过热

Δ T_{0}

（位于 Eqn. (2128) 中）。默认值为 1.0 K。

成核点密度限制

在高压条件下，成核点密度的计算值可能会变得不符合物理实际。要使计算的成核点密度保持在物理限制范围内，可以应用校正。默认情况下，此选项已启用。

请参见成核密度限制。

占位概率

指定成核点被某一增长气泡占据的概率。此值为 Eqn. (2145) 中的

f_{A T}

。默认值为 0.2。

Hibiki-Ishii 属性

Hibiki Ishii 模型是更高级的成核密度模型，适用于高达 198 bar 的压力。结合使用 Hibiki Ishii 模型与 Kocamustafaogullari 模型计算气泡脱离直径。

此模型具有以下特点：

它会考虑壁面过热的边界条件。
它已经过大量实验数据验证。
它在质量流量、压力和接触角方面具有广泛的应用性。

如果使用的是工作流体而非水，则调整壁面接触角。如果知道工作表面的平均空穴密度和空穴长度尺度值，则也调整这些项。

最大过热

设置传递至该子模型的壁面过热值的上限（请参见 Eqn. (2129)），防止在初始收敛过程中溢出。确保此限制不会影响收敛求解中预估的壁面过热值。

壁面接触角

为工作流体定义的数据。需要提供室温下的标称值。默认值 0.722 弧度 (41.37^o) 是供水系统的近似值（请参见 Eqn. (2132)）。

平均空穴密度

单位面积平均成核点数，用于计算成核密度（请参见 Eqn. (2132)）。可以对其进行调整以适合特定的表面质量。

壁面接触角尺度

为考虑对壁面接触角的依赖性而在模型中使用的参考值（请参见 Eqn. (2132)）。对于大多数应用，标准值为 0.722 弧度 (41.37^o)。

空穴长度尺度

计算成核密度时使用该值（请参见 Eqn. (2132)）。可以对其进行调整以适合特定的表面质量。

密度函数常数 C0、C1、C2 和 C3

为考虑计算成核密度时使用的压力而在模型中使用的值（请参见 Eqn. (2134)）。对于大多数应用，标准值为 -0.1064、0.48246、-0.22712 和 0.05468。

成核点密度限制

在高压条件下，成核点密度的计算值可能会变得不符合物理实际。要使计算的成核点密度保持在物理限制范围内，可以应用校正。默认情况下，此选项已启用。

请参见成核密度限制。

占位概率

指定成核点被某一增长气泡占据的概率。此值为 Eqn. (2145) 中的

f_{A T}

。默认值为 0.2。

气泡脱离直径属性

气泡脱离直径确定气泡离开成核点时的直径。

这是用于确定过冷沸腾中蒸发率的三个因子中的第二个（请参见 Eqn. (2110)）。下图说明了此参数：

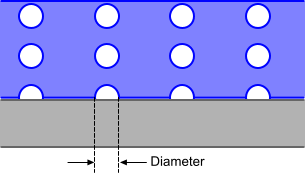
方法

用于计算气泡脱离直径的选项。

Tolubinsky Kostanchuk
Kocamustafaogullari
Unal
用户自定义：常数、场函数、表或用户程序。

Tolubinsky Kostanchuk 属性

Tolubinsky Kostanchuk 模型是基于液体过冷的相关性，也是从稳定性而言推荐用于初始研究的默认模型。它与默认的 Lemmert Chawla 模型一起用于计算成核密度。

参考直径: 计算气泡脱离直径时使用的参考直径（请参见 Eqn. (2150)），通过针对 45K 给定过冷的实验确定。
参考直径过冷: 在给定过冷值下计算气泡脱离直径时使用的参考直径过冷（即，参考直径的饱和温度与液体温度的区别）（请参见 Eqn. (2150)）。
最小直径: 设置气泡脱离直径的下限。此设置可确保结果在合理的限制范围内。
最大直径: 设置气泡脱离直径的上限。此设置可确保结果在合理的限制范围内。

Kocamustafaogullari 属性

Kocamustafaogullari 模型是基于力平衡的最新模型，使用更为普遍，针对压力依赖性进行了调整。选择 Hibiki Ishii 模型计算成核密度时必须使用此模型。

标定常数: 标定常数（请参见 Eqn. (2152)）。标准值为 1.5126x10^-3 米/弧度（2.64x10^-5 米/度）。
壁面接触角: 为工作流体指定的数据。需要提供室温下的标称值。默认值 0.722 弧度 (41.37^o) 是供水系统的近似值（请参见 Eqn. (2152)）。
如果使用的是工作流体而非水，则可根据需要调整壁面接触角。

Unal 属性

Unal 模型同时适用于低压和高压沸腾情景。无需参数调整。如果还要对气泡尺寸分布、破碎和聚结建模，则可以获取更好的预测结果。

参考直径过冷: 在给定过冷值下计算气泡脱离直径时使用的参考直径过冷（即，参考直径的饱和温度与液体温度的区别）。此值为 Eqn. (2153) 中的 $Δ T_{s u b}$ 。
最小直径: 设置气泡脱离直径的下限。此设置可确保结果在合理的限制范围内。
最大直径: 设置气泡脱离直径的上限。此设置可确保结果在合理的限制范围内。

气泡脱离频率属性

气泡脱离频率确定每秒离开成核点的气泡数。

这是在过冷沸腾中确定蒸发率的三个关键因子中的最后一个（请参见 Eqn. (2110)）。下图说明了此参数：

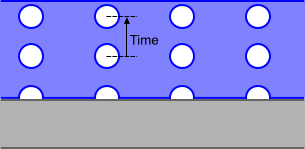
方法

用于计算气泡脱离频率的选项。

科尔：此频率等同于基于气泡脱离直径的终端速度比例，整体蒸发率围绕此假设进行校准（请参见 Eqn. (2155)）。没有可调参数，但可以定义替代模型。
用户自定义：常数、场函数、表或用户程序。

升空直径属性

对于离散相中选定的 S-Gamma 模型，升空直径确定气泡的直径，该直径提供给壁面中相应的颗粒尺寸分布模型。对应于 Eqn. (2306) 中的 $d_{l}$ 。

方法

用于计算升空直径的选项。

气泡脱离直径：将升空直径设为等于指定的气泡脱离直径属性。
场函数：可用于为尺寸分布模型指定与壁面沸腾模型不同的壁面气泡直径。

壁面瞬态传导属性

此模型可以校正气泡引发的淬火热通量，以便通过脱离气泡的操作来使用送至壁面的液体温度。此温度可以不同于在近壁网格单元中心计算的液体温度。校正在未受干扰的液相温度分布上远离脱离点的某个位置进行。

淬火温度选项

定义液体温度分布采样的位置。

壁面网格单元
近壁网格单元中心的液体温度用作淬火温度。这是默认设置。
固定的直径数
在指定作为固定的局部气泡脱离直径尺寸数的位置估计液体温度。在固定的直径数子节点中进行设置。
固定的 Yplus
在指定作为固定的液相壁面湍流长度尺度数的位置估计液体温度。在固定 Y+ 子节点中进行设置。

提供以下子节点：

气泡影响壁面面积分数
气泡引发的淬火热传递系数

气泡影响壁面面积分数属性

气泡影响壁面面积分数可估计扫掠脱离气泡下方流入的液体会影响的壁面积分数。

方法

用于计算气泡影响壁面面积分数的选项。

Kurul Podowski
用户自定义：常数、场函数、表或用户程序。

Kurul Podowski 属性

Kurul Podowski 模型按指定的因子假设受气泡引发的淬火影响的壁面面积大于成核面积（请参见 Eqn. (2158)）。

面积系数: 成核点面积密度和气泡影响的壁面面积密度的比率，通过 (Eqn. (2158)) 计算。默认值为 2.0。

气泡引发的淬火热传递系数属性

气泡离开受热面时，较冷的液体会填充气泡占据的空间。此过程中的热传递称为淬火热传递。淬火热传递系数用于计算淬火热通量。

方法

用于计算气泡引发的淬火热传递系数的选项。

Del Valle Kenning
用户自定义：常数、场函数、表或用户程序。

Del Valle Kenning 属性

此模型使用 Eqn. (2156) 计算气泡引发的淬火热传递系数。

等待系数: 一个气泡脱离与下一个气泡成核之间的气泡脱离循环周期的比例（请参见 Eqn. (2157)）。

边界设置

以下设置可用于壁面边界。

物理条件

壁面相间质量传递选项

激活壁面边界上的相间质量传递相互作用。

方法	对应的物理值节点
活动允许此边界上发生壁面沸腾。在[壁面边界名称] > 物理条件节点下，为相间相互作用中的每个相设置用户指定的壁面热通量系数。	无
无防止此边界上发生壁面沸腾。例如，当边界绝热时，使用此选项。	无

场函数

[相间相互作用]的气泡脱离直径: $d_{w}$ ，在 Eqn. (2150) 中（用于 Tolubinsky Kostanchuk 模型）或 Eqn. (2152) 中（用于 Kocamustafaogullari 模型）。
[相间相互作用]的气泡脱离频率: $f$ （位于 Eqn. (2155) 中）。
[相间相互作用]的气泡影响壁面面积分数: $K_{q u e n c h}$ （位于 Eqn. (2158) 中）。
Bubble Induced Quenching Heat Transfer Coefficient of [phase interaction]([相间相互作用] 的气泡引发的淬火热传递系数): $h_{q u e n c h}$ （位于 Eqn. (2156) 中）。
Bubble Induced Quenching Temperature Factor of [phase interaction]([相间相互作用] 的气泡引发的淬火温度因子): $s_{q u e n c h}$ （位于 Eqn. (2921) 中）。
[相间相互作用]的气泡引发的淬火温度距离: $y_{q u e n c h}$ （位于 Eqn. (2921) 中）。

Wall Dryout Area Fraction of [phase interaction]([相间相互作用] 的壁面干燥面积分数): $K_{d r y}$ （位于 Eqn. (2917) 中）。
[相间相互作用]的成核密度: $n ″$ ，在 Eqn. (2128) 中（用于 Lemmert Chawla 模型）或 Eqn. (2132) 中（用于 Hibiki-Ishii 模型）。
[相间相互作用]的 MMP 沸腾淬火热通量: ${q ″}_{q u e n c h}$ （位于 Eqn. (2923) 中）。
[相间相互作用]的 MMP 沸腾蒸发热通量: ${q ″}_{e v a p}$ （位于 Eqn. (2924) 中）。