多孔挡板

存在多孔介质厚度与其他尺寸相比较小的情况，例如通过多孔板或丝网的流。因此，可以假设流阻力和热传递是一维。流阻力的处理与多孔介质的处理类似。

对于多孔挡板，压降

Δ p

指定为：

图 1. EQUATION_DISPLAY

Δ p = - ρ (P_{i} | v_{s, n} | + P_{v}) v_{s, n}

(1858)

其中：

$v_{s, n}$ 为表面法向速度
$P_{i}$ 为多孔惯性阻力
$P_{v}$ 为多孔粘性阻力

系数 $P_{i}$ 和 $P_{v}$ 有效地定义了一维流的挡板渗透率。此方法假定通过挡板时流向不变。

通过多孔挡板，可以通过以下假设考虑热传导：

热传导是一维的
热惯性忽略不计
热传导的有效挡板面积由以下公式给出： $(1 - χ) \cdot solid surface area$

整个多孔挡板的总传热量因流体中的对流与扩散以及挡板的导热而被计算为热传递的线性组合。孔隙率

χ

提供了线性加权因子。此计算由以下公式给出：

图 2. EQUATION_DISPLAY

\dot{q} ″ = (1 - χ) \frac{Δ T}{(\frac{1}{h_{1}} + R_{th} + \frac{1}{h_{2}})} | a | + χ (k \nabla T) \cdot a - \dot{m} H

(1859)

其中：

$χ$ 为定义为孔面积与表面积之比的表面孔隙率
$Δ T$ 为挡板任一侧流体的温度差
$h_{1}, h_{2}$ 为挡板任一侧的传热系数
$R_{th}$ 为单位面积的热阻
$k$ 为挡板的导热率
$\dot{m}$ 为质量流率
$H$ 为流体焓

对于热传递分析，多孔挡板提供可以定义为有效电阻或由多层组成的接触热阻。每一层表示具有不同导热率的不同材料。热阻计算如下：

图 3. EQUATION_DISPLAY

\frac{1}{R_{th}} = \sum_{i = 1}^{n} \frac{k_{i}}{Δ x_{i}}

(1860)

其中 $k_{i}$ 和 $Δ x_{i}$ 分别为构成挡板的 $n$ 层中各层的导热率和厚度。

假设从基于阻力的多孔挡板生成的湍流控制了触及它的湍流，则使用以下方法近似计算多孔挡板下游侧的湍流物理量：

图 4. EQUATION_DISPLAY

\begin{matrix} k = I Δ v_{b}^{2} \\ ε = \frac{k^{3 / 2}}{l} \\ ω = \frac{1}{β^{*}} \frac{\sqrt{k}}{l} \end{matrix}

(1861)

其中：

$Δ v_{b} = | v_{b} - v_{s, b} |$ 是挡板处滑移速度的幅值（其中和分别是挡板速度和挡板处流体的表观速度）。 $v_{b}$ $v_{s, b}$
$I$ 为湍流强度。
$l$ 为湍流长度尺度。
$β^{*}$ 为 Eqn. (1214) 中的模型系数。

切向动量平衡

挡板的液压行为可由三维阻力张量来表征：

图 5. EQUATION_DISPLAY

R_{h} = [\begin{matrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{matrix}]

(1862)

将垂直于挡板的局部坐标轴表示为 $z$ 。分量 $R_{33}$ 是挡板的法向液压阻力，而分量 $R_{31}$ 和 $R_{32}$ 是升力系数，即它们负责与挡板平行的流导致的跨挡板的压降。假设一个无升力情景， $R_{h}$ 可以拆分为阻力 $R_{33}$ 的法向系数和二维张量：

图 6. EQUATION_DISPLAY

R_{| |} = [\begin{matrix} R_{11} & R_{12} \\ R_{21} & R_{22} \end{matrix}]

(1863)

下文中的下标 || 表示与挡板相切的二维歧管。

为了进一步简化模型，假设张量 $R_{| |}$ 为各向同性。因此，阻力张量的方程可写作：

图 7. EQUATION_DISPLAY

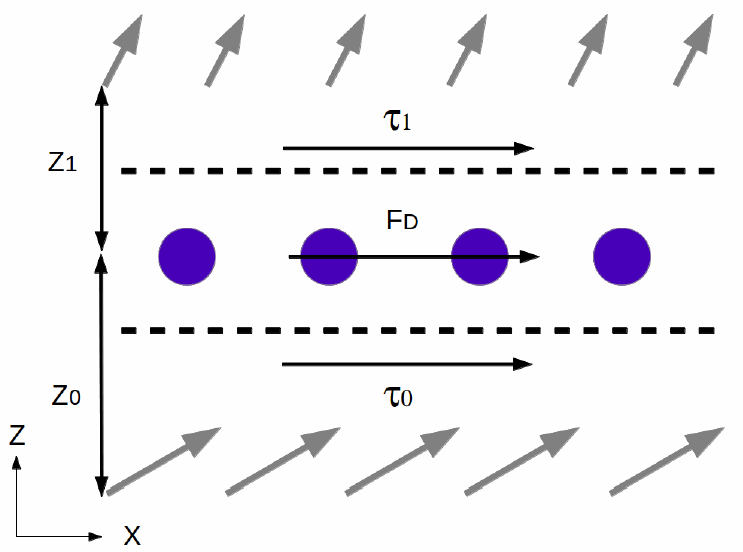
R_{h} = [\begin{matrix} R_{τ} & 0 & 0 \\ 0 & R_{τ} & 0 \\ 0 & 0 & R_{n} \end{matrix}]

(1864)

要设定交界面处的条件，可考虑如下所示的一排圆柱体。控制体积由虚线限定。最初，假设控制体积厚度有限，当其收缩到零时，得到的即为极限交界面条件。

有三个力作用于控制体积：两个剪切应力 $τ_{0}$ 、 $τ_{1}$ ，以及一个曳力 $F_{D}$ ：

图 8. EQUATION_DISPLAY

F_{D} = - R_{τ} {(u - V_{b})}_{| |} A

(1865)

其中 $V_{b}$ 为挡板的速度， $A$ 为多孔挡板交界面的表面积。

假设

图 9. EQUATION_DISPLAY

\begin{matrix} τ_{0} = - μ_{0} \frac{\partial u_{| |}}{\partial z} |_{0} & τ_{1} = μ_{1} \frac{\partial u_{| |}}{\partial z} |_{1} \end{matrix}

(1866)

力平衡可以写为：

图 10. EQUATION_DISPLAY

μ_{1} \frac{\partial u_{| |}}{\partial z} |_{1} - μ_{0} \frac{\partial u_{| |}}{\partial z} |_{0} = R_{τ} {(u |_{b} - V_{b})}_{| |}

(1867)

其中， ${u |}_{b}$ 是交界面处的速度，而 $μ$ 是有效粘度。

挡板附近的流场取决于切向阻力。如果切向阻力为 0，且挡板两侧的粘度相等，则 Eqn. (1867) 可得出：

图 11. EQUATION_DISPLAY

\frac{\partial u_{| |}}{\partial z} |_{1} = \frac{\partial u_{| |}}{\partial z} |_{0}

(1868)

而且，速度的切向分量跨挡板保持连续和平滑。

或者，对于 $R_{τ} \to \infty$ ，Eqn. (1867) 的 LHS 可以忽略，并且挡板会有效地在交界面处施加非滑移条件：

图 12. EQUATION_DISPLAY

{u |}_{b} = V_{b}

(1869)

切向相阻力

考虑上述曳力 $F_{D}$ 的表达式 (Eqn. (1865))，存在多相 $i$ 时：

图 13. EQUATION_DISPLAY

R_{τ} = ρ_{i} (α_{i, τ} | v_{i} | + β_{i, τ})

(1870)

其中：

$ρ_{i}$ 为相位密度
$v_{i}$ 为相位速度
$α_{i, τ}$ 为相位切向惯性阻力
$β_{i, τ}$ 为相位切向粘性阻力

相位切向阻力值的获取方式与相位法向阻力值相同，但在此情况下， $α_{m}$ 为多孔惯性切向阻力，而 $β_{m}$ 为多孔粘性切向阻力。 $α_{m}$ 和 $β_{m}$ 的值由用户指定。