稳健性和可靠性研究的采样方法
在稳健性和可靠性研究中,所有输入参数都是连续的。为每个参数指定分布值,采样方法根据指定的分布选择值。
在输入参数属性中,指定每个参数的分布值。有关更多详细信息,请参考:分布值(稳健性和可靠性研究)。
设置分布值时,关联的概率密度函数 (PDF) 和累积分布函数 (CDF) 已为此输入参数完全确定。
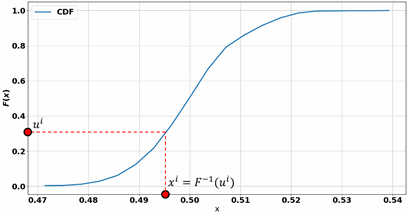
样本点(此输入参数的值)通过在 CDF 的反转函数 上映射 0 与 1 之间的随机样本点 来选择:
其中, 为 0 到 1 的随机样本,由计算机生成。
为与所需分布匹配的输入参数值。
从统计数据的角度来看,这些值更有可能来自 CDF 较陡峭的范围部分。
对于稳健性和可靠性研究,以下采样方法可用:
拉丁超立方采样
对于 m 个运行设计(样本大小),拉丁超立方体采样将分布函数 划分为面积相等的 段,并为每段选取一个值。下面显示了一个具有正态分布的输入参数和 5 个运行设计的示例:
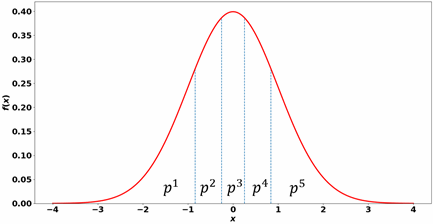
使用 CDF 从 到 的映射步骤如下所示:
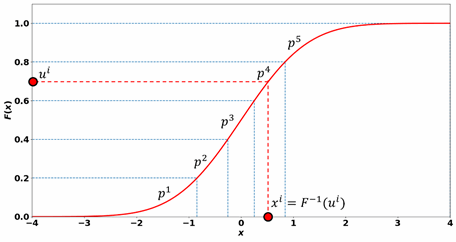
采样点 的选择介于 和 之间。
通常,对于拉丁超立方体采样, 。
在以上示例中, ,第四段的采样点 由值 生成。
以下绘图演示了不同样本大小在每个段内的设计所占百分比:
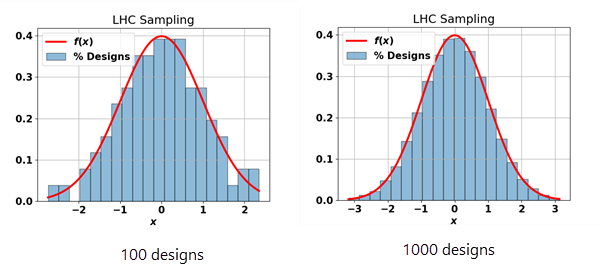
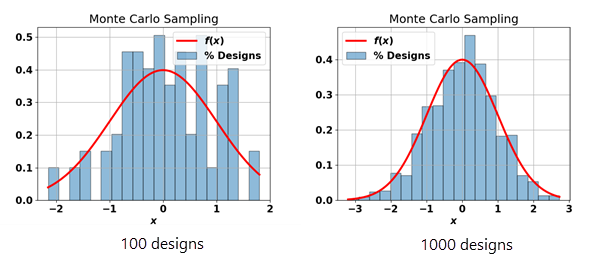
Monte Carlo 采样
Monte Carlo 采样方法从分布函数中生成独立的随机采样点,而不考虑先前生成的点。
Monte Carlo 采样方法的映射步骤如下所示:
每个值 均为从 0 到 1 的独立随机样本。
由于 Monte Carlo 采样方法的特性,需要较大的样本大小。
以下绘图演示了不同样本大小在每个段内的设计所占百分比: