DOE 研究的采样方法
实验设计 (DOE) 需要在特定范围内填充输入参数,而无需任何额外的参数分布。
对于 DOE 研究,以下采样方法可用:
| 采样方法 | 运行设计 | 适用性 | 设计点分布 |
|---|---|---|---|
| 2 级全因子 |
为输入参数的数量 |
计算主要效果和相互作用效果 | 主要位于设计空间的边或拐角上 |
| 3 级全因子 |
为输入参数的数量 |
计算主要效果和相互作用效果 | 主要位于设计空间的边或拐角上 |
| 拉丁超立方体采样(可选) | 由用户选择 | 构建响应表面 | 在设计空间中均匀分布 |
2 级全因子
2 级全因子设计指定每个输入参数的范围,其中包含两个值(层级)- 低和高。对于 个输入参数,设计运行总数为 ,其中将研究所有值组合。
3 级全因子
3 级全因子设计指定每个输入参数的范围,其中包含三个值(层级)- 低、中和高。对于 个输入参数,设计运行总数为 ,其中将研究所有值组合。
拉丁超立方体采样(可选)
此 DOE 研究类型要求选择参数类型:
- 恒定 - 为此输入参数指定恒值,而不浏览其他值。
- 离散 - 可以为此输入参数指定多个值,用逗号或空格分隔。尽可能在设计运行中均衡地使用这些值。
- 连续 - 为此输入参数指定值范围。
如果参数类型设为连续,则拉丁超立方采样方法将选择此输入参数的连续范围内的值。
在 DOE 设置中,指定运行设计的数量。如果存在 个运行设计(样本大小),则每个连续输入参数的范围将平均划分为 个间隔。Design Manager从每个间隔中选择一个值。
当存在多个输入参数时,设计的数量会增加。为保持效率,拉丁超立方采样算法从随机生成的样本中选择在设计空间中提供均匀分布的值组合。
例如,如果有两个输入参数 和 以及 5 个运行设计,则初始随机采样可能导致以下绘图中显示的一组设计研究:
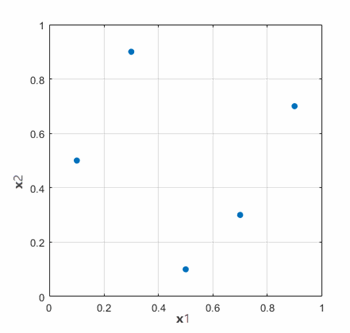
在初始分布中,采样点 3 和 4 彼此相对接近。拉丁超立方体算法检查设计点分布是否均匀,并改进样本选择。对于本例,拉丁超立方体方法将调整采样点,如下所示:
