代数多重网格

Simcenter STAR-CCM+ 提供了两种加速线性求解器的方法，即：适用于不可压缩流的预处理共轭梯度法和适用于所有其他流的稳定双共轭梯度法。

多重网格循环

多重网格方法支持通过在粗糙网格序列上使用简单校正扫掠，显著加速高斯-赛德尔等基本迭代格式的运行。粗糙级别访问策略可能会对该算法的效率产生很大的影响。Simcenter STAR-CCM+ 中使用的 AMG 求解器提供了两个循环策略，即固定和可变：

• 固定循环 — 完整的多重网格循环表示递归应用由以下步骤组成的单一循环：
  1. （预）平滑
  2. 限制
  3. 再循环
  4. 延长
  5. （后）平滑

  这些步骤将应用于一系列连续粗糙化的网格或方程组。平滑表示将任意数量的迭代松弛扫掠应用于当前精细级别上的方程，计算一组新校正。限制是指将现有残差向下传递到应用了新循环的下一个最粗糙级别。随后，结果校正将延长，即，传递回同样应用了平滑的当前精细级别。

  有以下三种类型的固定循环：

  • F 固定循环
  • V 固定循环
  • W 固定循环
• 可变循环 — 对于非刚性线性系统，此类循环是一种更经济的循环策略。每次在给定网格级别上扫掠后都会监视残差，而非按规则模式使用所有多重网格级别。如果残差减少率超出给定阈值，会继续在更粗糙的级别上求解。如果给定级别上的残差降幅超过指定阈值，则求解将转到更精细的级别。任何级别允许的扫掠数将进一步受到限制。

F 循环

F 循环是 W 循环的一种变体。此循环如下所示，涉及的粗糙级别扫掠数少于 W 循环，但仍多于 V 循环。

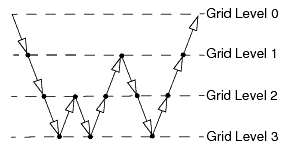
V 循环

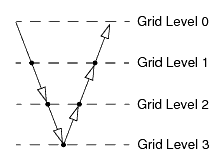
V 循环是最简单的固定循环类型，只有两个分支。在第一个分支中，用户对最精细的级别执行大量松弛扫掠并将残差传递到下一个级别。然后，对粗糙级别相继重复该操作，直至达到最粗糙的级别为止。粗糙“网格”通常仅包含几个“网格单元”。在最粗糙的级别上完成扫掠之后，使用得到的解校正下一个更精细级别上的求解。先在该级别执行一些松弛扫掠，然后重复此过程，直至达到最精细的级别为止。下图显示了此过程。

W 循环

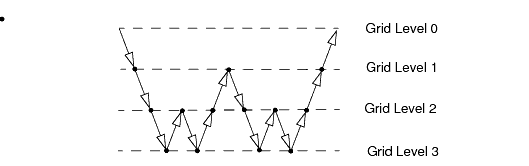
对于刚性方程组，V 循环有时不能满足需要，进行更多粗糙迭代非常有用。W 循环会增加粗糙松弛扫掠数，如下所示。

AMG 求解器

上述离散化方法的结果是一个线性系统：

表示每个计算网格单元的代数方程。矩阵 $\mathbf{\text{A}}$ 表示线性系统的系数，例如，Eqn. (920) 左侧的系数 $a_p$ 和 $a_n$ ，矢量 $\mathbf{\text{x}}$ 表示每个网格单元中的未知量（Eqn. (920) 中的 $\Delta \varphi$ ），矢量 $\mathbf{\text{b}}$ 表示每个网格单元中的残差（请参见 Eqn. (921)）。

可使用雅可比、高斯-赛德尔或不完全上下三角分解松弛格式（更平滑）求解结果线性方程组。

雅可比和高斯-赛德尔

迭代方法背后的一般原则是：给定近似求解 ${\mathbf{\text{x}}}^k$ ，找到更精确的近似值 ${\mathbf{\text{x}}}^{k+1}$ ，然后重复该过程。

如果迭代 k 的误差定义为：

$${\mathbf{\text{e}}}^k=\mathbf{\text{x}}-{\mathbf{\text{x}}}^k$$

(978)

其中， $\mathbf{\text{x}}$ 将精确解和残差表示为：

$${\mathbf{\text{r}}}^k=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}^k$$

(979)

由此得出：

$${\mathbf{\text{A}}\mathbf{\text{e}}}^k={\mathbf{\text{r}}}^k$$

(980)

因此，继续迭代且直到残差趋向于较小的值为止，从而得出一个较小的误差值。

最基本的迭代方法是雅可比和高斯-赛德尔迭代。这些方法涉及按顺序访问每个网格单元，然后使用 n 个相邻网格单元的系数更新每个网格单元中的 $x_i$ 值 i，如下所示：

$$x_i=\frac{1}{A_{i,i}}(b-{\sum }_{\text{neighbors }n}^{}{A}_{i,n}{x}_n)$$

(981)

雅可比和高斯-赛德尔迭代之间的区别很小：雅可比使用 $x_n$ 的“旧”值，而高斯-赛德尔则使用已更新的可用值，从而改进收敛。

不完全上下三角 (ILU)

ILU（不完全 LU）法 Saad [283] 使用以下方程迭代求解 ${\mathbf{\text{x}}}^{k+1}$ ：

$$\widetilde{\mathbf{\text{A}}}\left({\mathbf{\text{x}}}^{k+1}-{\mathbf{\text{x}}}^k\right)=b-\mathbf{\text{A}}{\mathbf{\text{x}}}^k$$

(982)

其中

$$\widetilde{\mathbf{\text{A}}}=\mathbf{\text{L}}\mathbf{\text{U}}=(\mathbf{\text{D}}+{\mathbf{\text{L}}}_A)(\mathbf{\text{I}}+{\mathbf{\text{D}}}^{-1}{\mathbf{\text{U}}}_A)$$

(983)

其中， $\mathbf{\text{I}}$ 为单位矩阵， ${\mathbf{\text{L}}}_A$ 和 ${\mathbf{\text{U}}}_A$ 为原始矩阵 $\mathbf{\text{A}}$ 的上下三角矩阵， $\mathbf{\text{D}}$ 为使用 MILU(0) 方法计算得出的对角矩阵。

与高斯-赛德尔方法相比，ILU 方法的计算成本更高，但更稳定。ILU 方法的稳定性意味着可以在三个维度中处理组尺寸 8 或更大，而高斯-赛德尔方法只能处理组尺寸 4。使用 ILU 方法处理复杂问题，改进收敛和并行可扩展性。对于三维问题，可将其用于组尺寸 8。

加速方法

预处理共轭梯度法

为了在压力求解器中加速线性系统的迭代求解收敛，提供了共轭梯度法，该方法使用 AMG 求解器作为预调节器。此方法用于不可压缩流（恒密度模型）和分离流模型。

要求解线性系统 $\mathbf{\text{A x }}=\mathbf{\text{b}}$ ，预处理共轭梯度 (PCG) 采用以下形式：

$${\mathbf{\text{r}}}_0=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}_0$$

(984)

$${\mathbf{\text{z}}}_0\cong \text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{r}}}_0)$$

(985)

$${\mathbf{\text{p}}}_0={\mathbf{\text{z}}}_0$$

(986)

$$\mathbf{\text{k}}=0$$

(987)

每次迭代涉及到通过 Eqn. (994) 计算 Eqn. (988)：

$${\alpha }_k=\frac{\left({\mathbf{\text{r}}}_k^T{\mathbf{\text{z}}}_k\right)}{\left({\mathbf{\text{p}}}_k^T\text{A}{\mathbf{\text{p}}}_k\right)}$$

(988)

$${\mathbf{\text{x}}}_{k+1}={\mathbf{\text{x}}}_k+{\alpha }_k{\mathbf{\text{p}}}_k$$

(989)

$${\mathbf{\text{r}}}_{k+1}={\mathbf{\text{r}}}_k-{\alpha }_k\mathbf{\text{A}}{\mathbf{\text{p}}}_k$$

(990)

如果 $\left|{\mathbf{\text{r}}}_{k+1}\right|<\epsilon$ ，则迭代将结束。

$${\mathbf{\text{z}}}_{k+1}\cong \text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{r}}}_{k+1})$$

(991)

$${\beta }_k=\frac{\left({\mathbf{\text{r}}}_k^{+}{\mathbf{\text{z}}}_{k+1}\right)}{\left({\mathbf{\text{r}}}_k{\mathbf{\text{z}}}_k\right)}$$

(992)

$${\mathbf{\text{p}}}_{k+1}={\mathbf{\text{z}}}_{k+1}+{\beta }_k{\mathbf{\text{r}}}_k$$

(993)

$$k=k+1$$

(994)

线性系统的解为 ${\mathbf{\text{x}}}_{k+1}$ 。

收敛 PCG 算法的必要条件是矩阵 $\mathbf{\text{A}}$ （在这里也是预调节器）为对称正定 (SPD)。在纯不可压缩案例中，压力求解器的线性系统矩阵满足此条件。

迭代过程中的 Eqn. (985) 和 Eqn. (991) 是预调节器求解器计算，它们涉及一个 AMG 固定循环，用于近似估计辅助线性系统：

$${\mathbf{\text{Az}}}_k={\mathbf{\text{r}}}_k\text{ k}=0,1,\dots$$

(995)

正如已实施的那样，PCG 可加速收敛并提高压力求解器的并行可扩展性。正常情况下（不存在非线性不稳定性），PCG 预计不会显著改变 Simcenter STAR-CCM+ 的整体非线性收敛。如果由于压力求解器的线性系统缺乏完全收敛而导致数值不稳定，PCG 可以提供稳定收敛。

稳定双共轭梯度法

如今已开发稳定双共轭梯度 (BiCGStab) 法，用于求解非对称（常规）线性系统。Simcenter STAR-CCM+ 采用 AMG 预处理 BiCGStab 算法提高求解器生成的线性系统的稳定性和收敛速度。

要求解常规线性系统 $\mathbf{\text{A x }}=\mathbf{\text{b}}$ ，预处理 BiCGStab 执行以下步骤：

$${\mathbf{\text{r}}}_0=\mathbf{\text{b}}-{\mathbf{\text{Ax}}}_0$$

(996)

$$\tilde{\text{r}}={\mathbf{\text{r}}}_0$$

(997)

$$i=0$$

(998)

每次迭代 $i$ 涉及到通过 Eqn. (1012) 计算 Eqn. (999)：

$${\rho }_{i-1}={\tilde{\text{r}}}^T{\mathbf{\text{r}}}_{i-1}$$

(999)

如果 ${\rho }_{i-1}=0$ ，则该方法将失败。

如果 $i=1$ ：

$${\mathbf{\text{p}}}_i={\mathbf{\text{r}}}_{i-1}$$

(1000)

否则，根据 Eqn. (1001) 和 Eqn. (1002)：

$${\beta }_{i-1}=\left(\frac{{\rho }_{i-1}}{{\rho }_{i-2}}\right)\left(\frac{{\alpha }_{i-1}}{{\omega }_{i-1}}\right)$$

(1001)

$${\mathbf{\text{p}}}_i={\mathbf{\text{r}}}_{i-1}+{\beta }_{i-1}\left({\mathbf{\text{p}}}_{i-1}-{\omega }_{i-1}{\mathbf{\text{v}}}_{i-1}\right)$$

(1002)

$$\hat{\text{p}}=\text{AMG fixed cycle }(\mathbf{\text{A}},{\mathbf{\text{p}}}_i)$$

(1003)

$${\mathbf{\text{v}}}_i=\mathbf{\text{A}}\cdot \hat{\text{p}}$$

(1004)

$${\alpha }_i=\frac{{\rho }_{i-1}}{({\tilde{\text{r}}}^T\cdot {\mathbf{\text{v}}}_i)}$$

(1005)

$$\mathbf{\text{S}}={\mathbf{\text{r}}}_{i-1}-({\alpha }_i\cdot {\mathbf{\text{v}}}_i)$$

(1006)

如果 $(\left|\mathbf{\text{S}}\right|<\epsilon )$ ，根据 Eqn. (1007)：

$${\mathbf{\text{x}}}_i={\mathbf{\text{x}}}_{i-1}+{\alpha }_i\hat{\text{p}}$$

(1007)

迭代将结束。

否则，迭代将继续，如下所示：

$$\hat{\text{S}}=\text{AMG fixed cycle }(\mathbf{\text{A}},\mathbf{\text{S}})$$

(1008)

$$\mathbf{\text{t}}=\text{A}\cdot \hat{\text{S}}$$

(1009)

$${\omega }_i=\frac{{\mathbf{\text{t}}}^T\cdot \mathbf{\text{S}}}{{\mathbf{\text{t}}}^T\cdot \mathbf{\text{t}}}$$

(1010)

$${\text{x}}_i={\mathbf{\text{x}}}_{i-1}+{\alpha }_i\hat{\text{p}}+{\omega }_i\mathbf{\text{S}}$$

(1011)

$${\mathbf{\text{r}}}_i=\mathbf{\text{S}}-{\omega }_i\mathbf{\text{t}}$$

(1012)

如果 $\left|{\mathbf{\text{r}}}_i\right|<\epsilon$ ，则迭代将结束。

如果 ${\omega }_i\ne 0$ ，则迭代将继续。

线性系统的解为 ${\mathbf{\text{x}}}_i$ 。

迭代过程中的 Eqn. (1003) 和 Eqn. (1008) 是预调节器求解器计算，它们涉及一个 AMG 固定循环，分别用于获得以下两个方程的近似求解：

$$\mathbf{\text{A}}\cdot \hat{\text{p}}={\mathbf{\text{p}}}_i\text{ and }\text{A}\cdot \hat{\text{S}}=\text{S}\text{ respectively}$$

(1013)

正如预处理共轭梯度法一样，如果由于线性系统收敛不足而导致数值不稳定，BiCGStab 可以提高并行可扩展性并改进收敛。

预处理广义最小残差法

与预处理稳定双共轭梯度法类似，广义最小残差法 (GMRes) 方法可以求解一般、不一定对称的线性系统。Simcenter STAR-CCM+ 采用 AMG 预处理 GMRes 算法提高求解器生成的线性系统的稳定性和收敛速度，如 [283] 第 9.3.1 章所述。

注意，与预处理共轭梯度和稳定双共轭梯度方法相比，预处理 GMRes 法提高了内存需求。